Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа № 246 Приморского района Санкт-Петербурга
«Как решать задачи по теории вероятностей в ЕГЭ по математике?»
Р абота учителя математики
абота учителя математики
Зориной Елены Борисовны
Задачи по теории вероятностей включены в ЕГЭ по математике под номером 10 для базового уровня и под номером 4 для профильного уровня.
Для решения данных задач необходимо знать лишь базовые понятия теории вероятностей. Таким образом, с ними в состоянии справится, без преувеличения, каждый ученик.
Для начала определение: случайное событие - это событие, которое нельзя точно предсказать. Оно может либо произойти, либо нет.
Например, Вы получили подарок, оказавшись тысячным покупателем в бутике — это случайное событие. Либо Вы выиграли в лотерею - случайное событие.
Однако, очевидно, что для любого случайного события есть какая-то вероятность, с которой оно может произойти. Если лотерейный билет купило 150.000 человек, а выиграли Вы один, то вероятность - 1 к 150.000. То есть интуитивно понятно, что такое вероятность события.
Рассмотрим примеры.
Бросаем монету. Выпадет либо орел… либо решка... Такое действие, которое может привести к одному из нескольких результатов, в теории вероятностей называют испытанием. Орел и решка — два возможных исхода испытания (все варианты событий, которые только могут произойти, монета не может ни зависнуть, ни встать на ребро).
Возвращаясь к нашей монете, можно сказать, орел выпадет в одном случае из двух возможных. Говорят, что вероятность того, что монетка упадет орлом, равна 1/2. Так же вероятность выпадения решки 1/2.
Следующий пример: игральная кость.
У кубика всего шесть граней, поэтому возможных исходов шесть (кубик может упасть только на одну из шести граней).
Выпадение одного очка это один исход из шести возможных. Выпадение двух очков, это один исход из шести возможных. В теории вероятности такой исход называется благоприятным исходом.
Вероятность выпадения тройки так же равна 1/6 (один благоприятный исход из шести возможных). Вероятность четверки — тоже 1/6. А вот вероятность появления семерки равна нулю. Ведь грани с семью точками на кубике нет.
Игральные карты.
Возьмём колоду из 36 карт. Вероятность того, что Вы вытащите из колоды карт одну, которую загадали, равна один к тридцати шести или 1/36, тридцать шесть это число возможных исходов, которые могут произойти (число всех карт), один это число благоприятных исходов (загаданная карта).
Вероятность того, что вы вытащите из колоды карт туза, равна 4 к 36 или 4/36. Четыре это число благоприятных исходов (в колоде четыре туза), тридцать шесть - число возможных исходов.
Вероятность того, что вы вытащите из колоды карт красную карту (черви или буби) равна 1 к 2 или 1/2. Число благоприятных исходов 18 (красных карт ровно половина), возможных исходов также 36, 18/36=1/2.
Вероятность события равна отношению числа благоприятных исходов к числу всевозможных исходов.
Понимания этого определения вполне достаточно, чтобы решить задачи В10.
Очевидно, что вероятность не может быть больше единицы.
Вот еще пример. Есть 23 шара одинакового размера, из них 8 — красных, остальные — зеленые. Вы наугад берете один шар. Вероятность того, что это окажется красный шар равна 8/23, а зеленый — 15/23.
Вероятность взять красный или зеленый шар равна 8/23 + 15/23 = 1.
Ну а теперь переходим к решению самих прототипов В10.
Прежде чем начать, я еще раз хочу повторить ключевой формулу, необходимую для решения задач В10: "Вероятность события равна отношению числа благоприятных исходов к числу всевозможных исходов."
Она настолько важна, что я ее оставлю в рамочке.
Начну с простых задач. Не буду на них долго задерживаться.
Итак, задача:
Брошена игральная кость. Какова вероятность того, что выпадет чётное число очков?
1, 3, 5 — нечетные числа; 2, 4, 6 — четные. Число возможных исходов при бросании игральной кости 6. Число благоприятных исходов 3 (выпадение двойки, четвёрки или шестёрки). Таким образом, вероятность выпадения четного числа очков равна три к шести или 0,5.
Ответ: 0,5
Брошена игральная кость. Какова вероятность того, что выпадет число меньше 4?
Другими словами, какова вероятность того, что выпадет либо единица, либо двойка, либо тройка? Число возможных исходов 6. Число благоприятных исходов 3 (выпадение единицы, двойки или тройки). Таким образом, вероятность выпадения числа меньшего четырёх будет 3 к 6 или 3/6=0,5.
Ответ: 0,5
В ящике 6 белых и 4 чёрных шара. Какова вероятность того, что первый наудачу выбранный шар окажется белым?
Всего шаров 10, значит число возможных исходов 10. Число благоприятных исходов 6 (в ящике 6 белых шаров). Вероятность того, что первый выбранный шар окажется белым 6 к 10, то есть 6/10=0,6
Ответ: 0,6
Набирая номер телефона, абонент забыл последнюю цифру. Какова вероятность того, что он правильно дозвонится, набрав последнюю цифру наугад?
Абоненту нужно выбрать одну из десяти цифр, то есть число возможных исходов 10. Число благоприятных исходов 1 (верной может быть только одна цифра). Вероятность того, что он правильно дозвонится равна 1 к 10 или 0,1.
Ответ: 0,1
Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число 56?
Число возможных исходов 100 (сто чисел). Верно названное число одно это 56, значит благоприятный исход один. Вероятность того, что он назовёт число 56 будет один к ста или 0,01.
Ответ: 0,01
Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число кратное пяти?
Число возможных исходов 100 (сто чисел). Чисел кратных пяти двадцать (перечислим):5,10,15,20,25,30,35,40,45,50,55,60,65,70,75,80,85,90,95,100. То есть число благоприятных исходов 20. Вероятность того, что ученик назовёт число кратное пяти равна 20 к 100 или 20/100=0,2.
Ответ: 0,2
Ученика попросили назвать число от 1 до 100. Какова вероятность того, что он назовёт число, принадлежащее промежутку от 5 до 20 включительно?
Число возможных исходов 100. Число благоприятных исходов 16: это числа от 5 до 20 (5,6…..19,20), причём 5 и 20 входят в промежуток (в условии сказано «от 5 до 20 включительно»). Искомая вероятность равна 16/100.
Ответ: 0,16
В фирме такси в данный момент свободно 10 машин: 5 чёрных, 1 жёлтая и 4 зелёных. На вызов выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.
Возможное число исходов 10. Число благоприятных исходов 1 (жёлтая машина одна). Искомая вероятность равна 1 к 10 или 0,1.
Ответ: 0,1
Валя выбирает трёхзначное число. Найдите вероятность того, что оно делится на 51.
Число возможных исходов это количество трёхзначных чисел. Их существует от 100 до 999, быстрее всего их можно посчитать так: 1000-1-99=900 (исключаем тысячу и числа от 1 до 99). То есть число всевозможных исходов: 900. Найдем, сколько трехзначных чисел делится на 51. Если мы поделим 999 - самое большое трехзначное число - на 51, то получим приблизительно 19 целых пятьдесят восемь сотых. То есть в 999 вмещается 19 чисел, кратных 51. Но среди них есть и само число 51, которое не является трехзначным. А значит трехзначных чисел, делящихся на 51 - 18.
Число благоприятных исходов 18. Вероятность искомого события равна 18 к 900, или 18/900=0,02.
Ответ: 0,02
При двукратном бросании игрального кубика в сумме выпало 6 очков. Найдите вероятность того, что первый раз выпало меньше трёх очков.
Сумму в шесть очков можно получить следующими способами (переберём варианты): 1+5, 2+4, 3+3, 4+2, 5+1 - всего их пять, это и есть число возможных исходов. Из представленных вариантов также видно, что менее трёх очков при первом броске может выпасть только в двух случаях. Искомая вероятность равна 2 к 5 или 0,4.
Ответ: 0,4
Монету бросают трижды. Найдите вероятность того, первые два броска окончатся одинаково.
Найдём число возможных исходов, переберём все варианты бросков. В подобных задачах составляйте таблицу, так считать на много удобней.
|
| 1-й бросок | 2-ой бросок | 3-ий бросок |
| 1 | орёл | орёл | орёл |
| 2 | орёл | орёл | решка |
| 3 | орёл | решка | решка |
| 4 | орёл | решка | орёл |
| 5 | решка | решка | решка |
| 6 | решка | решка | орёл |
| 7 | решка | орёл | орёл |
| 8 | решка | орёл | решка |
Всего возможных исходов восемь.
Первые два броска одинаково могут окончится в четырёх случаях это 1,2,5,6 варианты, то есть благоприятных исходов 4. Искомая вероятность равна 4/8=0,5.
Обратите внимание, что если в условие добавить одно только слово, смысл задачи изменится, многие из-за невнимательности решают неверно. Итак:
Монету бросают трижды. Найдите вероятность того, что только первые два броска окончатся одинаково.
Благоприятных исходов будет 2, это 2-й и 6-й варианты, первый и пятый варианты исключаются из-за этого «только».
В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
В данной задаче составляется та же таблица, что и предыдущей. Орёл не выпадет ни разу только в одном варианте из восьми (пятый вариант). Искомая вероятность равна 1 к 8 или 0,125.
Ответ: 0,125
В среднем на 150 карманных фонариков приходится три неисправных. Какова вероятность купить исправный фонарик.
Количество возможных исходов 150. Количество благоприятных исходов 150-3=147 (на 150 приходится 147 исправных). Вероятность купить исправный фонарик 147 к 150 или 147/150=49/50=0,98
Ответ: 0,98
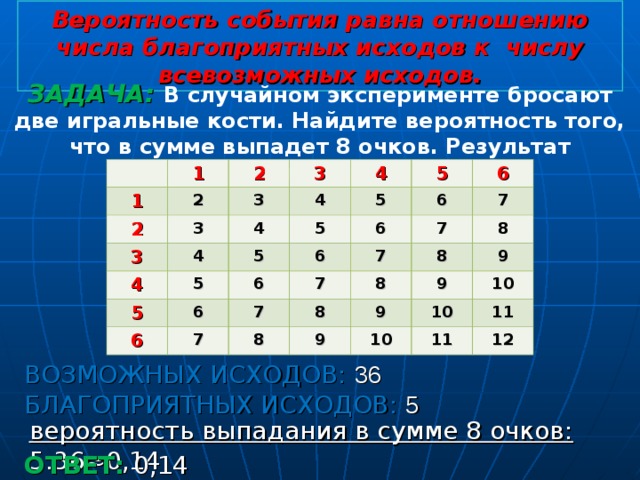
В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
В подобных задачах для удобства следует составить таблицу сумм для двух костей (все варианты сумм, которые могут выпасть):
| | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Всего исходов 36 (6 на 6). Благоприятных исходов 5 (легко подсчитать в таблице). Вероятность того, что в сумме выпадет 8 очков, равна 5 к 36 или 0,13888888…. Округляем до сотых, получаем 0,14.
Ответ: 0.14
В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные — из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Давайте представим, что все спортсменки одновременно подошли к шляпе и вытянули из нее бумажки с номерами. Кому-то из них достанется первый номер. Вероятность того, что его вытянет китайская спортсменка равна 5 к 20, то есть 5/20 (поскольку из Китая — 5 спортсменок).
Ответ: 0,25
Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений — по одному от каждой страны. В первый день 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
Выясним, как распределятся выступления по дням:
1 день – 8 выступлений, остальные поровну, значит по 18 выступлений в день. Вероятность, что выступление представителя России состоится в третий день конкурса, равна 18 к 80 или 18/80=0,225.
Ответ: 0,225
На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов определяется жеребьёвкой. Найдите вероятность того, что восьмым окажется доклад ученого из России.
Восьмым может оказаться любой учёный, значит возможных исходов 10 (их всего 10). Из России приехало трое, значит благоприятных исходов три. Вероятность того, что восьмым окажется доклад ученого из России 3 к 10 или 0,3.
Ответ: 0,3
Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России?
В данном случае нужно поставить себя на место Руслана Орлова.
Он будет играть кем-то из 25 спортсменов (на чемпионат приехали Руслан и ещё 25 спортсменов), значит возможных исходов 25. Из них осталось 9 спортсменов из России. Это и есть число благоприятных исходов. Вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России 9 к 25 или 0,36.
Ответ: 0,36

 Получите свидетельство
Получите свидетельство Вход
Вход











































 Методическая разработка с презентацией "Как научиться решать задачи по теории вероятностей" (1.37 MB)
Методическая разработка с презентацией "Как научиться решать задачи по теории вероятностей" (1.37 MB)
 0
0 769
769 39
39 Нравится
0
Нравится
0



