ТОГАПОУ «Промышленно-технологический колледж»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
открытого урока
по дисциплине «Математика»
по теме: «Физический смысл производной»
для студентов специальности:
15.02.15 «Технология металлообрабатывающего производства»
Подготовил
преподаватель:
Е.А. Шмакова
Мичуринск- 2018
Тема урока: «Физический смысл производной»
Цели:
Обучающая. знакомство с историей открытия производной; основными направлениями применения производной в разных областях науки и техники, закрепление понятия производной функции, основных формул и правил дифференцирования, геометрического и механического смысла производной; формирование ОК 1-7, ПК 1.2, 2.1 по теме в системе тестов, дифференцированных по степени сложности.
Развивающая. Развитие умений применять знания в конкретной ситуации; развитие логического мышления, развитие монологической речи, развитие навыка работы в группе, умение работать в проблемной ситуации; развитие умения сравнивать, обобщать, правильно формулировать задачи и излагать мысли; развитие самостоятельной деятельности студентов.
Воспитательная. Формирование у студентов ответственного отношения к учению; умения работать в коллективе, взаимопомощи, культуры общения; воспитание таких качеств характера, как настойчивость в достижении цели; развитие устойчивого интереса к математике; создание положительной внутренней мотивации к изучению математики.
Задачи:
учить применять полученные теоретические знания для решения задач;
учить анализировать условие задачи с тем, чтобы выбрать оптимальный вариант решения;
научить защищать выполненную работу;
осуществлять контроль своих знаний с помощью компьютерных тестов;
учить использовать компьютерные технологии для устной самостоятельной работы с целью проверки усвоения теории по данной теме;
научить работать в группе.
Оборудование:
ПК преподавателя,
Мультимедийный проектор,
ПК студентов.
Плакаты «Производные элементарных функций», «Формулы дифференцирования»,
Раздаточный материал с дифференцированными заданиями. Тесты.
Презентация темы.
Карточки для рефлексии настроения и результативности.
Тип урока: урок обобщения и систематизации знаний.
Методы обучения:
проблемное обучение
частично-поисковый метод
Принцип обучения: принцип политехнизма
План урока
Организационный момент.(1 мин).
Целеполагание и мотивация.(2 мин).
3. Доклад по теме: «Исторические сведения о возникновении дифференциального исчисления» (3 мин)
4. Актуализация опорных знаний (3 мин).
Работа по теме урока. (11 мин).
Закрепление изученного материала. (20 мин).
Совместный разбор задачи
Самостоятельное решение задачи
Подведение итогов урока (3 мин.)
Домашнее задание (2 мин).
Организационный момент.
Вступительное слово преподавателя:
Обсуждение темы занятия.
Ребята, отгадайте ключевое слово урока
1) С её появлением математика перешагнула из алгебры в математический анализ;
2) Ньютон назвал её «флюксией» и обозначал точкой;
3) Бывает первой, второй,… ;
4) Обозначается штрихом.
Итак, сегодня на уроке мы поговорим о производной, о её применении.
Производная функции - одно из важнейших понятий математического анализа.
Производная характеризует скорость изменения функции по отношению к изменению независимой переменной.
В геометрии производная характеризует крутизну графика, в механике – скорость неравномерного прямолинейного движения, в биологии – скорость размножения колонии микроорганизмов, в экономике – отзывчивость производственной функции (выход продукта на единицу затрат), в химии – скорость химической реакции.
Надеюсь, что сегодняшний урок, поможет вам понять происходящее и подготовит к адекватному восприятию производной, имеющее практическую направленность, ориентированное на ваш жизненный опыт, и поможет ответить на вопрос: «Так ли важно изучать тему «Производная»?».
Сообщение цели урока.
Как вы думаете, ребята, какова цель нашего урока?
( Студенты формулируют цель.)
Цель нашего урока – повторить основные формулы и правила дифференцирования, узнать основные направления применения производной в разных областях науки и техники.
Рассмотрим на примерах решения задач, как применяется производная в математике, химии, физике, биологии, географии, экономике, машиностроении.
Как в математике называют действие нахождения производной функции?
Дифференцирование
Историческая справка
Доклад студента
Метод дифференциального исчисления был создан в XVII - XVIII вв.
С возникновением этого метода связаны имена двух великих математиков - И. Ньютона и Г.В. Лейбница.
Сэр Исаак Ньютон (англ. Sir Isaac Newton), 4 января 1643 года - 31 марта 1727 года) - английский физик, математик, механик и астроном, один из создателей классической физики. Автор фундаментального труда "Математические начала натуральной философии", в котором он изложил закон всемирного тяготения и три закона механики, ставшие основой классической механики. Разработал дифференциальное и интегральное исчисления, теорию света и многие другие математические и физические теории.
Готфрид Вильгельм Лейбниц (нем. Gottfried Wilhelm Leibniz); 21 июня (1 июля) 1646 - 14 ноября 1716) - немецкий философ, логик, математик, механик, физик, юрист, историк, дипломат, изобретатель и языковед. Основатель и первый президент Берлинской Академии наук, иностранный член Французской Академии наук .Ввёл большую часть современной символики математического анализа.
Лейбниц пришёл к понятию производной, решая задачу проведения касательной к произвольной линии, объяснив этим ее геометрический смысл.
Но это не говорит о том, что до них эти вопросы не изучались. Задолго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, применяя при этом предельные переходы, но и сумел найти максимум функции.
Эпизодически понятие касательной встречалось в работах итальянского математика И.Тартальи.
В 17в. на основе учения Г.Галилея активно развилась кинематическая концепция производной. Понятие производной встречается уже у Р.Декарта, французского математика Роберваля, английского учёного Д.Грегори, в работах И.Барроу.
Большой вклад в изучение дифференциального исчисления внесли Лопиталь, Бернулли, Лагранж, Эйлер, Гаусс, Коши. Необходимо сказать, что ни Ньютон ни Лагранж не дали четкого определения производной. Впервые определение производной было сформулировано Коши, и именно это определение стало общепринятым и в настоящее время используется почти во всех курсах анализа.
(Презентация «История производной»)
а) Что называется производной функции в точке?
Ответ: производной функции у = f(x) в точке х0 называется предел отношения приращения функции в точке х0 к приращению аргумента, когда последнее стремится к нулю.
Я еще раз повторю это определение, но только в стихотворной форме.
| В данной функции от х, нареченной игреком, | y = f(x) |
| Вы фиксируете икс, отмечая индексом. | x0 |
| Придаете вы ему тотчас приращение, | x0 + ∆x |
| Тем у функции самой, вызвав изменение. | ∆y = f (x0 + ∆x) - f (x0) |
| Приращений тех теперь, взявши отношение, | ∆y : ∆x |
| Пробуждаете к нулю у ∆x стремление. | ∆x → 0 |
| Предел такого отношенья вычисляется, |
|
| Он производною в науке называется. | y′ = |
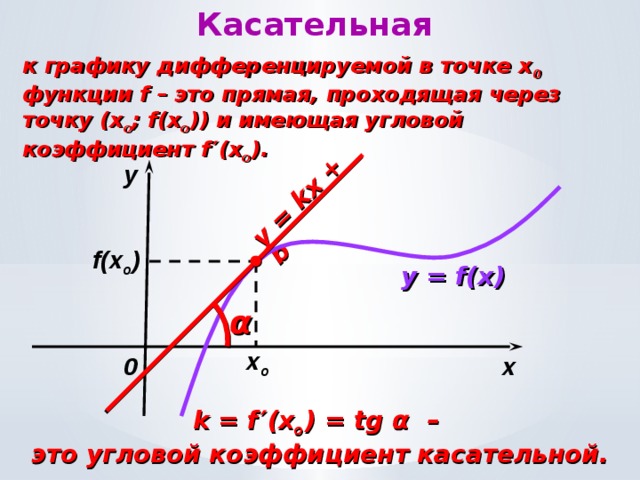
б) В чем заключается геометрический смысл производной?
Ответ: значение производной f '(x) при данном значении аргумента x равно тангенсу угла, образованного с положительным направлением оси Ox касательной к графику функции f(x) в точке M(x, f(x)). k = tg = f '(x0).
в) В чем заключается механический смысл производной?
Ответ: производная функции y = f(x) в точке x0 - это скорость изменения функции f (х) в
точке x0 , т.е. x'(t) = (t)
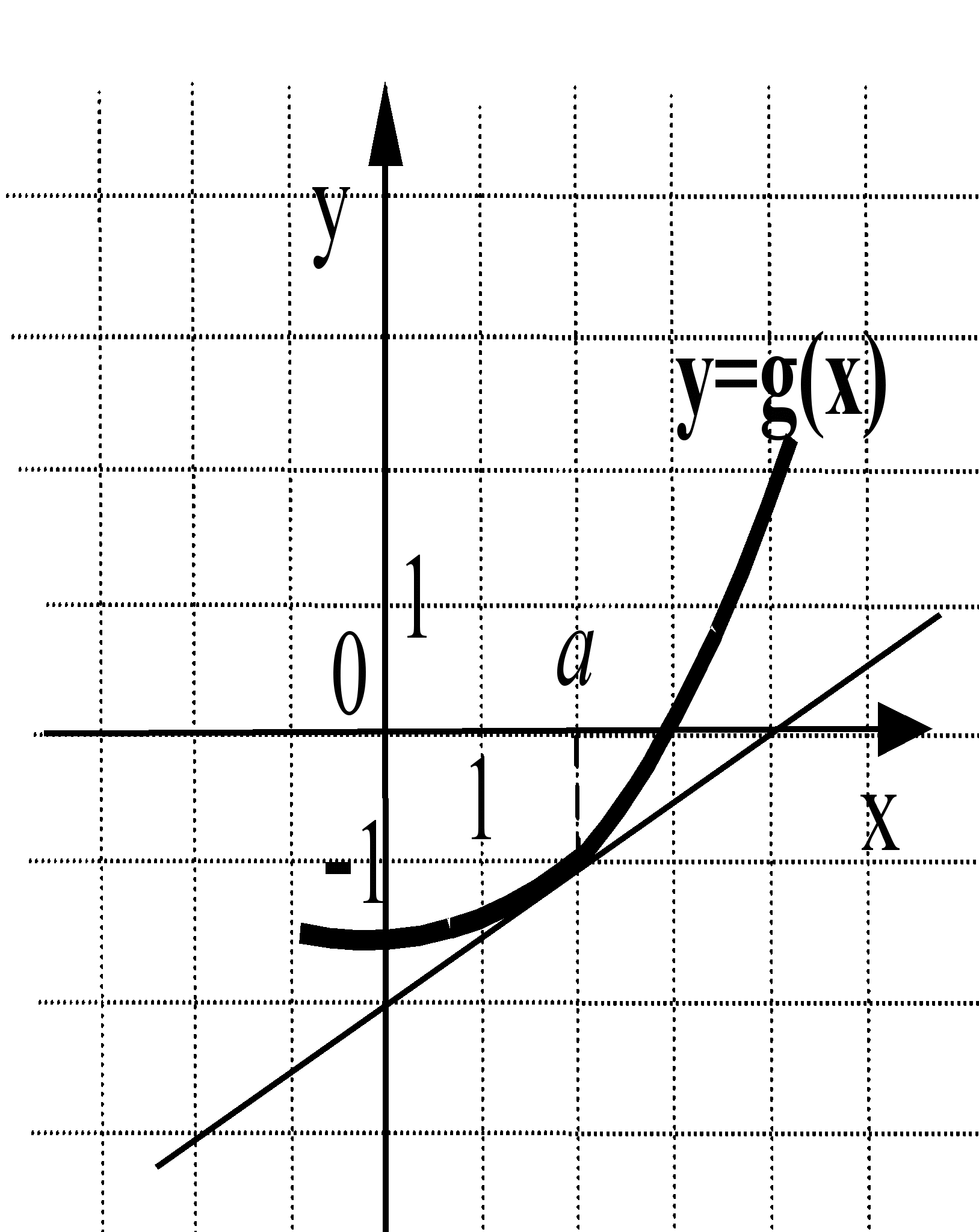
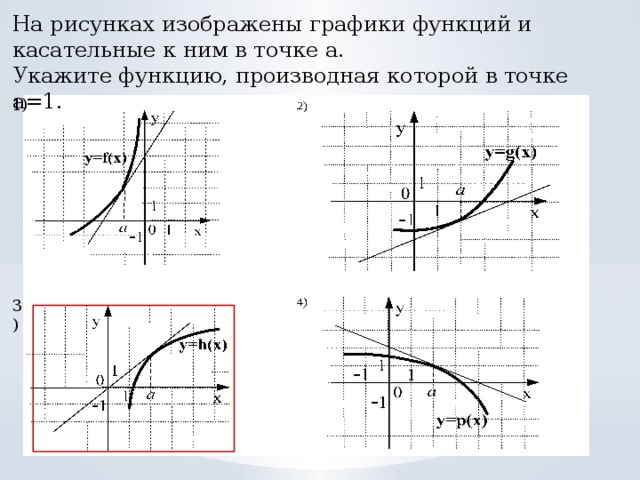
г) На рисунках изображены графики функций и касательные к ним в точке а. Укажите функцию, производная которой в точке а равна 1.
Ответ: (3)
|
|
|
|
|
|
|
|
|
|
| Найдите производную функции: | Ответы: |
|
| И 1 +
Р 3x
3 2x2
Ф 12x2 Ю С 1 -
Я 5х4 +12х3 - 2 К - Н
Л x3
М 4x3 |
Ф.И.студента_________________________________
| Номер задания | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Ответ (буква) |
|
|
|
|
|
|
|
Сообщения студентов
Производная в геометрии:
1. Касательная к графику функции 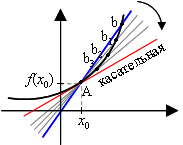
Касательная к графику функции f, дифференцируемой в точке xо, - это прямая, проходящая через точку (xо; f(xо)) и имеющая угловой коэффициент f ′(xо).
y = f(xо) + f ′(xо) (x – xо)
2. Пароход “Челюскин” в феврале 1934 года успешно прошел весь северный морской путь, но в Беринговом проливе оказался зажатым во льдах. Льды унесли “Челюскин” на север и раздавили.
Вот описание катастрофы: “Крепкий металл корпуса поддался не сразу, – сообщал по радио начальник экспедиции О.Ю. Шмидт. – Видно было, как льдина вдавливается в борт, и как над ней листы обшивки пучатся, изгибаясь наружу.
Лед продолжал медленное, но неотразимое наступление. Вспученные железные листы обшивки корпуса разорвались по шву. С треском летели заклепки. В одно мгновение левый борт парохода был оторван от носового трюма до кормового конца палубы…”
Почему произошла катастрофа?
Сила Р давления льда (рис. на доске – плакат) разлагается на две: F и R. R – перпендикулярна к борту, F – направлена по касательной. Угол между P и R – 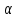 – угол наклона борта к вертикали.
– угол наклона борта к вертикали.
Q – сила трения льда о борт.
Q = 0,2 R (0,2 – коэффициент трения).
Если Q F, то трение мешает скольжению льдины, и лед может смять и продавить борт.
0,2R , tg 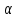 0,2
0,2
Q 110.
Наклон бортов корабля к вертикали под углом 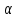 110 обеспечивает безопасное плавание во льдах.
110 обеспечивает безопасное плавание во льдах.
(В это время на компьютере заставка – рисунок № 1).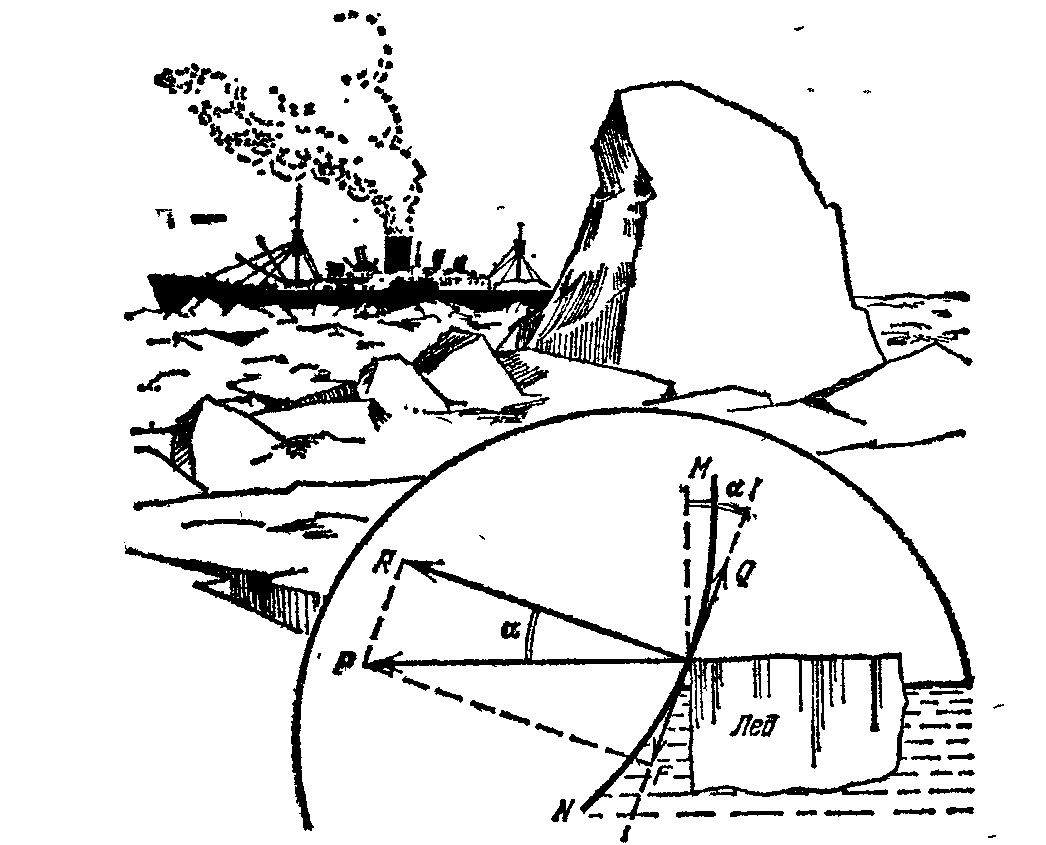
Производная в физике:
υ(t) = х/(t) – скорость
a (t) = υ/ (t) - ускорение
I(t) = q/(t) - сила тока
C(t) = Q/(t) - теплоемкость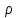 (l) = m/(l) - линейная плотность
(l) = m/(l) - линейная плотность
K (t) = l/(t) - коэффициент линейного расширения
ω (t)= φ/(t) - угловая скорость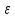 (t) = ω/(t) - угловое ускорение
(t) = ω/(t) - угловое ускорение
N(t) = A/(t) – мощность
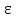 = -Ф/ (t) –ЭДС
= -Ф/ (t) –ЭДС
П (t) = V / (t) - производительность труда,
где V (t) - объем продукции
J(x) = y / (x) - предельные издержки производства,
где y– издержки производства в зависимости от объема выпускаемой продукции x.
Производная в химии:
И в химии нашло широкое применение дифференциальное исчисление для построения математических моделей химических реакций и последующего описания их свойств.
Производную в химии используют для определения очень важной вещи – скорости химической реакции, одного из решающих факторов, который нужно учитывать во многих областях научно-производственной деятельности. V (t) = p ‘(t)
Производная в биологии:
Популяция – это совокупность особей данного вида, занимающих определённый участок территории внутри ареала вида, свободно скрещивающихся между собой и частично или полностью изолированных от других популяций, а также является элементарной единицей эволюции.
Р = х‘ (t)
Производная в географии:
Производная помогает рассчитать:
1. Некоторые значения в сейсмографии
2. Особенности электромагнитного поля земли
3. Радиоактивность ядерно- геофизических показателей
4.Многие значения в экономической географии
5.Вывести формулу для вычисления численности населения на территории в момент времени t.
у’= к у
Идея социологической модели Томаса Мальтуса состоит в том, что прирост населения пропорционально числу населения в данный момент времени t через N(t) .Модель Мальтуса неплохо действовала для описания численности населения США с 1790 по 1860 годы. Ныне эта модель в большинстве стран не действует
Производная в электротехнике:
В наших домах, на транспорте, на заводах: всюду работает электрический ток. Под электрическим током понимают направленное движение свободных электрически заряженных частиц.
Количественной характеристикой электрического тока является сила тока.
В цепи электрического тока электрический заряд меняется с течением времени по закону
q=q (t).
Сила тока I есть производная заряда q по времени.
I(t) = q/(t) - cила тока
В электротехнике в основном используется работа переменного тока.
P(t) = A/(t) - мощность электрического тока
Электрический ток, изменяющийся со временем, называют переменным. Цепь переменного тока может содержать различные элементы: нагревательные приборы, катушки, конденсаторы.
Получение переменного электрического тока основано на законе электромагнитной индукции, формулировка которого содержит производную магнитного потока.
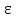 = -Ф/ (t) - ЭДС
= -Ф/ (t) - ЭДС
Производная в экономике:
Экономика – основа жизни, а в ней важное место занимает дифференциальное исчисление – аппарат для экономического анализа. Базовая задача экономического анализа – изучение связей экономических величин в виде функций.
Производная в экономике решает важные вопросы:
1. В каком направлении изменится доход государства при увеличении налогов или при введении таможенных пошлин?
2. Увеличится или уменьшится выручка фирмы при увеличение цены на её продукцию?
Для решения этих вопросов нужно построить функции связи входящих переменных, которые затем изучаются методами дифференциального исчисления.
П (t) = V / (t) - производительность труда,
где V (t) - объем продукции
J(x) = y / (x) - предельные издержки производства,
где y– издержки производства в зависимости от объема выпускаемой продукции x.
Также с помощью экстремума функции (производной) в экономике можно найти наивысшую производительность труда, максимальную прибыль, максимальный выпуск и минимальные издержки.
Самостоятельная работа в группах
Работа в группах
Сегодня на нашем уроке работают 5 творческих групп, у каждой из них есть своя тема.
Физики
Технологи
Химики
Электрики
Экономисты
Дифференцированные задания для групп
Задачи для физиков
на оценку «3»
Задача. Автомобиль приближается к мосту со скоростью 72 км/ч. У моста висит дорожный знак "36 км/ч". За 7 с до въезда на мост, водитель нажал на тормозную педаль. С разрешаемой ли скоростью автомобиль въехал на мост, если тормозной путь определяется формулой
s=20t-t2?
Решение.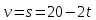
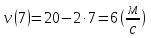
Да, т.к. скорость через 7 с будет равна 6м/с (21,6 км/ч).
на оценку «4»
Задача. Материальная точка движется по закону:
х(t) = 5 - 3t2 + 2t3 . Ускорение ее равно 6 м/с2
а) Выведите формулу для вычисления скорости движения точки в любой момент времени t
( t 0).
б) Найдите скорость в момент t = 2c;
в) Через сколько секунд после начала движения точка остановится?
Г) Есть ли в задаче лишние данные?
Д) Допущена ли ошибка в условии задачи?
Е) Найдите ускорение в момент t = 2c
Решение:
S = S(t); Скорость V = S′(t) = x′(t); ускорение а = v′(t) = х″(t).
v(t) = x′(t) = - 6t + 6t2; V(2) = - 6∙2 + 6∙4 = 12 (м/с);
- 6t + 6t2=0
- 6t(1-t)=0
t = 0 или t=1 c
a(t) = - 6 + 12t; a(2) = -6 + 12∙2 = 18(м/с2).
Ответ: v = 12 м/с; 1 c; а = 18м/с2.
на оценку «5»
Задача. Тело движется по закону 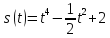 .Найдите моменты времени, в которые равнодействующая сил, действующих на тело равна нулю.
.Найдите моменты времени, в которые равнодействующая сил, действующих на тело равна нулю.
Когда равнодействующая сил, действующих на тело равна нулю?
Как при этом движется тело?
- равномерно прямолинейно, т.е. с постоянной скоростью;
-тело покоится, т.е. скорость тела равна нулю.
Тогда задача сводится к нахождению скорости тела.
Решение: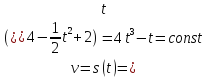 .
.
Если
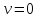 , то
, то 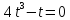
t(4t2-1)=0
t=0
t=0,5 с
t= - 0,5 с не соответствует условию задачи.
2)v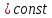 , т.е.a=0
, т.е.a=0
a(t) = v`(t)=(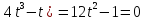
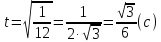
Ответ: t=0 , t=0,5 с,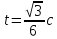
Задачи для химиков
на оценку «3»
Задача. Пусть количество вещества, вступившего в химическую реакцию задается зависимостью: р(t) = t2/2 + 3t –3 (моль).
Найти скорость химической реакции через 3 секунды.
Решение: р`(t) =( t2/2 + 3t –3)` = t+3
р`(3) = 3+3= 6 (моль/c)
на оценку «4»
Задача. Определить скорость радиоактивного распада, если задан закон радиоактивного распада N (t)=N0 e-λt , где λ=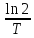 , N0 = 106, T – период полураспада
, N0 = 106, T – период полураспада
Решение: N`(t)=(N0 e-λt)` = N0 e-λt(--λt)`= -λ N0 e-λt
Какие необходимы данные для получения числового значения?
на оценку «5»
решить обе задачи.
Задачи для электриков
на оценку «3»
Задача. Количество электричества, протекающее через проводник, задаётся формулой
q(t) = t+4/t. В какой момент времени ток в цепи равен нулю?
Решение:
I(t) = q / (t),
I(t) = 1 - 4/t2
1 - 4/t2 =0
Отсюда, t = 2 или t = 2; t = -2 не подходит по условию задачи
на оценку «4»
Задача. Сила тока в цепи рассчитывается по формуле: I = 320/(20 +R). Найти, как быстро меняется сила тока при изменении внешнего сопротивления R, т.е. найти производную данной функции при R = 200 Ом.
Решение: I` = (320/(20 +R))` = 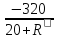
I`(200) = 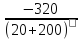 =
= 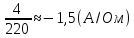
Ответ: 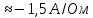
Что показывает знак «минус» в ответе?
Сила тока убывает.
на оценку «5»
решить обе задачи.
Задачи для технологов
на оценку «3»
Задача. Вращающееся маховое колесо, задерживаемое тормозом, за t секунд поворачивается на угол 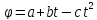 . Определить момент остановки колеса.
. Определить момент остановки колеса.
Решение. 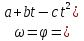 =b-2ct
=b-2ct
b-2ct=0
2ct=b
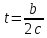
на оценку «4»
Задача. Пусть Q (t) количество теплоты, которое необходимо для нагревания тела массой 1 кг от 00С до температуры t0 (по Цельсию), известно, что в диапазоне 00 0, формула Q (t) = 0,396t+2,08110-3t2-5,024×10-7t3 дает хорошее приближение к истинному значению. Найдите, как зависит теплоёмкость воды от t.
Решение. C (t) = Q / (t) = 0,396 + 4,162*10 -3 t – 15,072*10 -7 t2
на оценку «5»
Задача. Зависимость модуля упругости материала от температуры задано формулой :
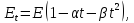
где 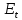 модуль упругости при температуре t,
модуль упругости при температуре t,
E- модуль упругости при комнатной температуре,
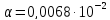
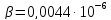 .
.
Определить быстроту изменения модуля упругости материала при нагревании.
Что необходимо найти в данной задаче?
Производную функции 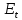
Всё ли нам известно для нахождения данной величины?
Нет. Мы не знаем E- модуль упругости при комнатной температуре
А как его можно узнать?
Найти его в справочной литературе.
Этим вы будете заниматься при изучении спецдисциплин. А мы сейчас решим задачу с учетом того, что Е=const
Решение:
Задачи для экономистов
на оценку «3»
Задача. Оборот предприятия за истекший год описывается через функцию
U (t) =0,15t3- 2t2 + 200, где t - месяцы, U-миллионы.
Исследуйте оборот предприятия за 9 и 10 месяцы.
Решение. Исследуем оборот предприятия с помощью производной: U' (t) =0,45t2 - 4t
Меньший оборот был на девятом месяце - 0,45. На 10 месяце - 5.
на оценку «4»
Задача. Объем продукции V цеха в течение дня зависит от времени по закону
V(t) = -5/3t3+15/2t2+50t+70, где 1
Вычислите производительность труда П при t =7 ч.
Решение:
П (t) = V / (t)
П (t) = -5t2 + 15t + 50
П (7) = -5*49 + 15*7 + 50 = - 90 (ед/ч)
Что показывает знак «минус» в ответе?
на оценку «5»
решить обе задачи.
Итог урока (рефлексия результативности, настроения)
Подведение итогов занятия
Объявление оценок
Задание на дом
Рефлексия
- Каким вопросам был посвящен урок?
- Чему научились на уроке?
- Какие теоретические факты обобщались на уроке?
Тему «Производная» очень важно изучать, потому что производная функции
используется всюду, где есть неравномерное протекание процесса: это и неравномерное механическое движение, и переменный ток, и химические реакции и радиоактивный распад вещества и т.д.
Мы убедились в важности изучения темы "Производная", ее роли в исследовании процессов науки и техники, в возможности конструирования по реальным событиям математической модели, и решать важные задачи.
Сегодня на уроке получили следующие оценки: (называю студентов и оценки).
Задание на дом:
[3] с. 67-68
Решить задачу:
Задача. Материальная точка массой 0,01 кг совершает гармонические колебания по закону косинуса с периодом 2сек и начальной фазой равной нулю. Полная энергия колеблющейся точки 1*10-4 Дж. Найти амплитуду колебаний; написать уравнение данных колебаний; найти наибольшее значение силы, действующей на точку.
Из приведенной ниже таблицы выберите элемент, составьте и решите задачу на применение производной.
Изотоп
Период полураспада
Актиний
10 суток
Йод
8 суток
Кальций
164 суток
Кобальт
5,3 года
Магний
10 минут
Полоний
138 суток
Радий
1590 лет
Радон
3,82 суток
Стронций
27 лет
Уран-235
7,1
108 лет
Уран-238
4,5
109 лет
Фосфор
14,3 суток
Церий
285 суток
Составить условие задачи, связанное с вашей специальностью, и решить ее, использовав физический смысл производной.
Повторить правила дифференцирования и таблицу производных.
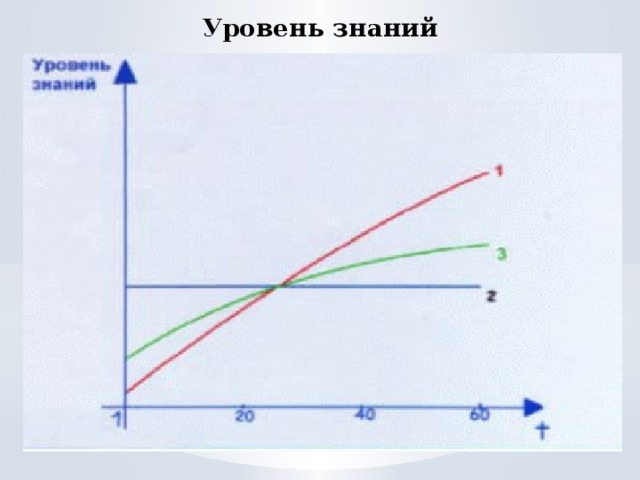
И, наконец, после “всяких умных вещей” немного юмора. На экране представлены графики зависимости уровня ваших знаний от времени, в интервале от начала урока до его завершения. Пожалуйста, выберите тот график, который, на ваш взгляд, наиболее близок вам, принимая во внимание их разный характер.
- Имеют ли они отношение к теме нашего урока?
- Можно ли по этим графикам судить о скорости приращения наших знаний в ходе урока? – Если – да, то как?
Перед вами карточки.
Если вы считаете, что хорошо потрудились на уроке, разобрались в методах применения производной к решению различных задач, то выбираете карточку № 1.
Если осталось что-то неясно, однако, вы научились вычислять производную, то выбираете карточку № 3.
Если вам урок не понравился и вы для себя ничего нового не узнали, то выбираете карточку № 2.
- Какой же график выбран вами? Если вы выбрали график 1 – это означает, что мы достигли цели и решили задачи, поставленные в начале урока.
Я же довольна сегодняшним уроком, потому что организовала вашу работу так, что вы самостоятельно добыли знания, научились решать практические задания.
Рефлексия настроения.
Ребята, поскольку мы достигли цели нашего урока, то настроение у меня вот такое: (показываю карточку № 1). 1
- А какое настроение у вас?
Мне приятно было с вами работать, и надеюсь, что знания, полученные на уроках математики, вы сможете применить в дальнейшей своей жизни. 2 3
Спасибо за урок!
Литература
Алимов Ш.А. Алгебра и начала анализа: 10-11 М.: Просвещение, 2007
Апанасов П.Т. Сборник задач по математике: Учебное пособие для техникумов - М.: Высшая школа, 2007
Богомолов Н.В. Практические занятия по математике: Учебное пособие для средних учебных заведений Высшая школа, 2007.
Яковлев Г.Н. Математика для техникумов Алгебра и начала анализа - М.: Наука, 2007
Данко П.Е. Высшая математика в упражнениях и задачах - М: ОНИКС Мир и образование, 2009
14

 Получите свидетельство
Получите свидетельство Вход
Вход



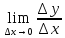
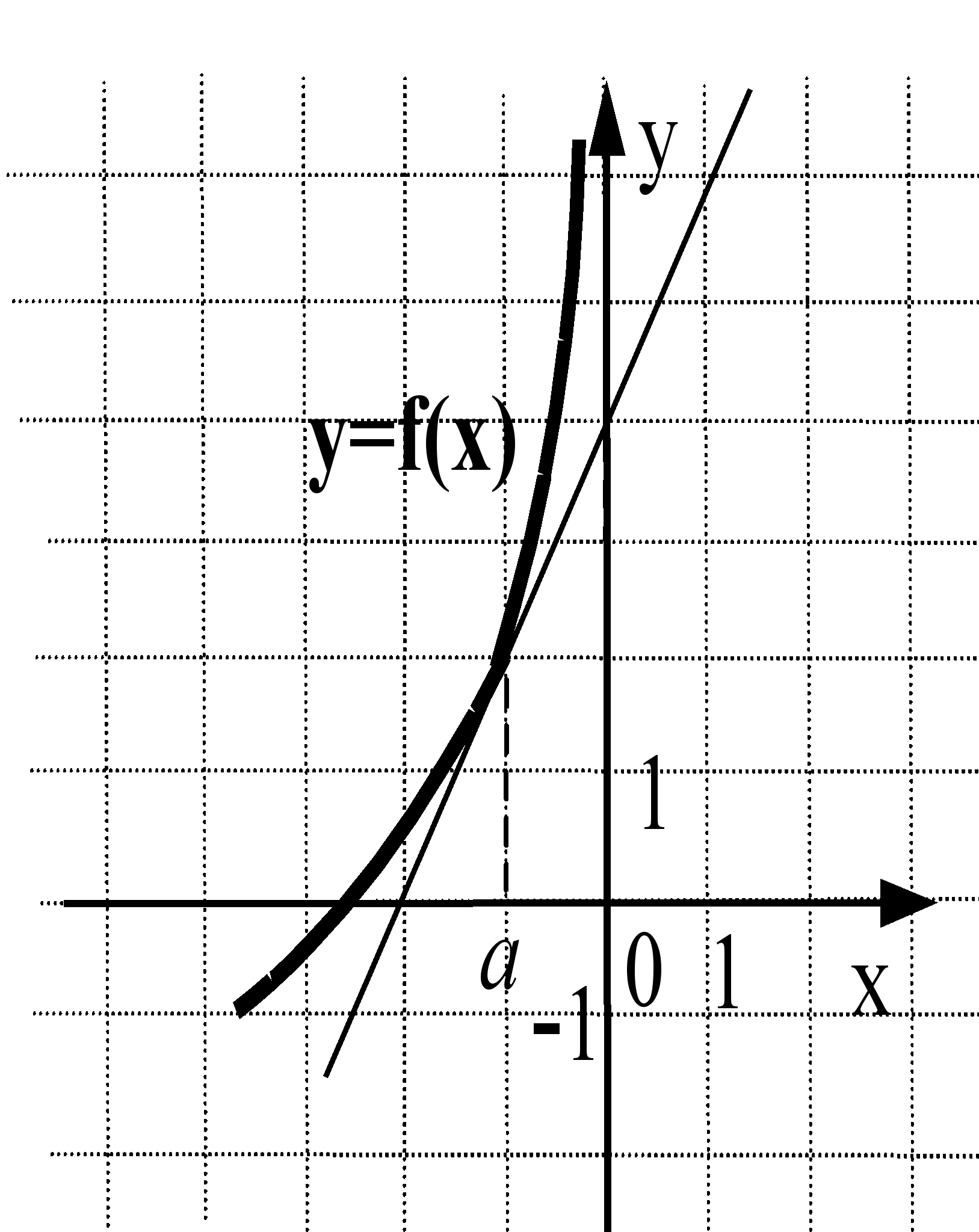
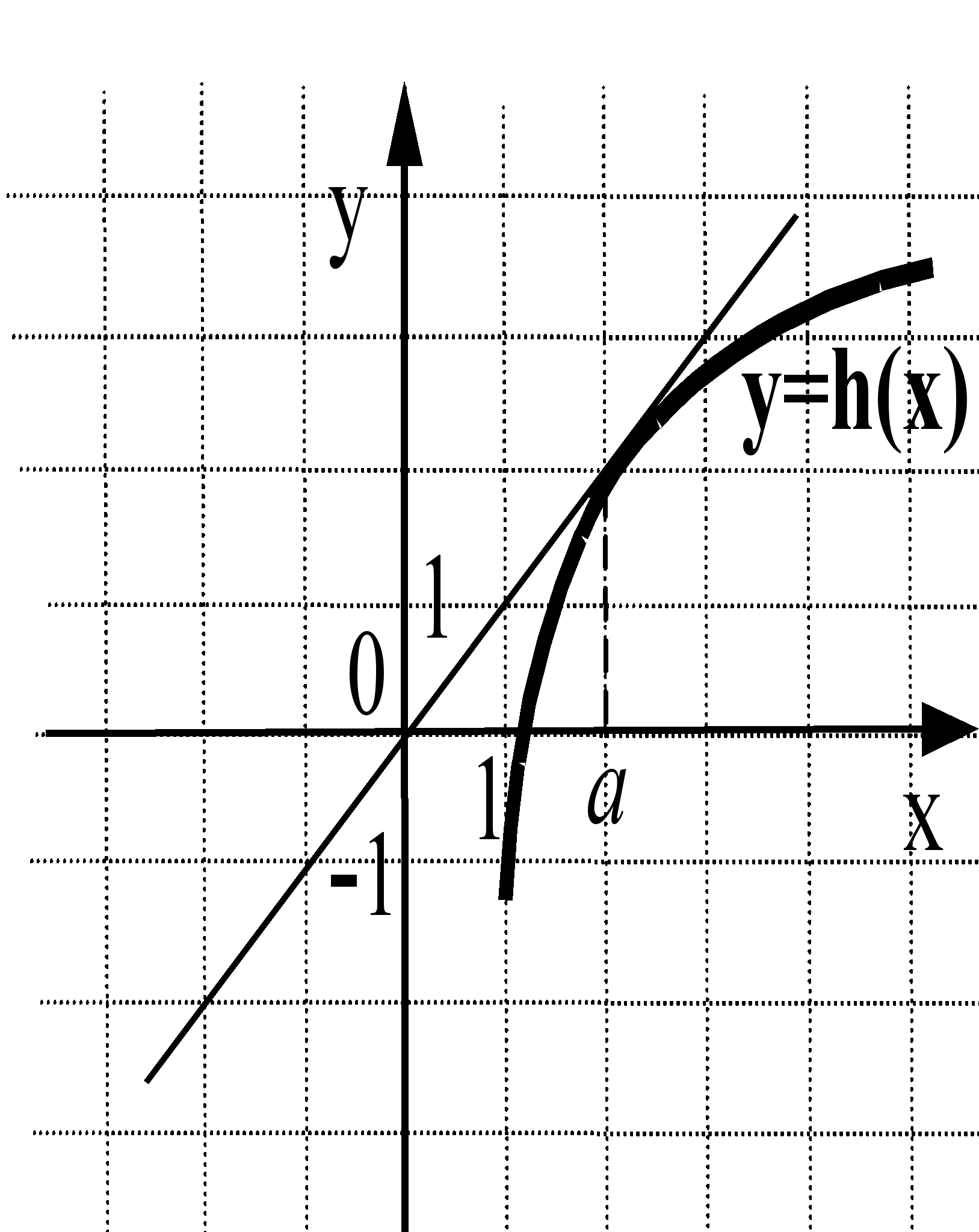
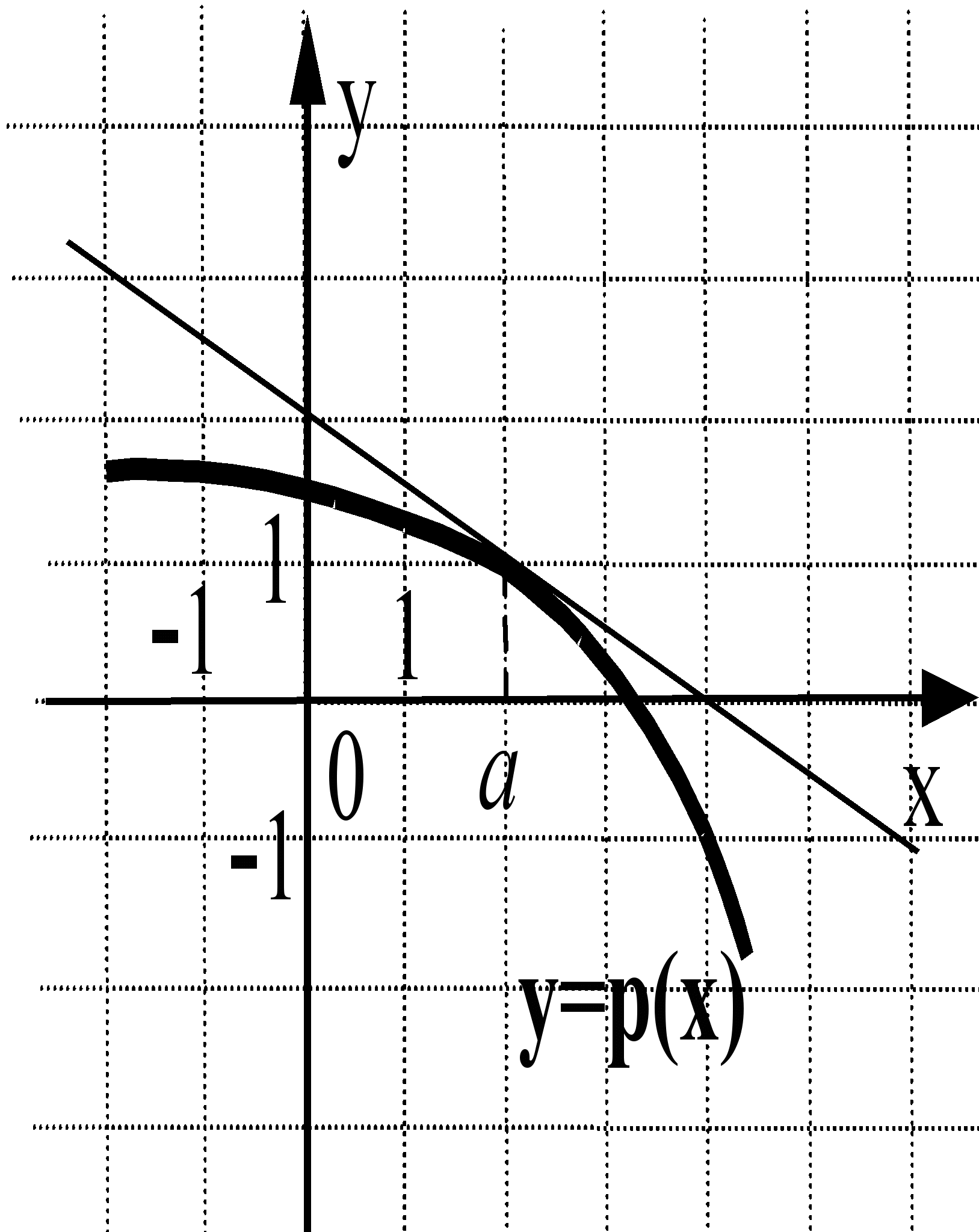
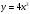
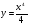
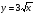
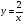
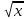
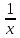
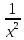
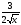
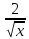
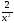
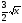






















 0 ). б) Найдите скорость в момент t = 2c ; в) Через сколько секунд после начала движения точка остановится? Г) Есть ли в задаче лишние данные? Д) Допущена ли ошибка? Е) Найдите ускорение в момент t = 2c Решение: Скорость v = x′(t); ускорение а = v′(t) = х″(t). v(t) = x′(t) = - 6t + 6t 2 ; v(2) = - 6∙2 + 6∙4 = 12 (м/с); =0 t=0 или t=1 (с) a(t) = - 6 + 12t; a(2) = -6 + 12∙2 = 18(м/с 2 ). Ответ: v = 12 м/с; t= 1 c; а = 18м/с 2 ." width="640"
0 ). б) Найдите скорость в момент t = 2c ; в) Через сколько секунд после начала движения точка остановится? Г) Есть ли в задаче лишние данные? Д) Допущена ли ошибка? Е) Найдите ускорение в момент t = 2c Решение: Скорость v = x′(t); ускорение а = v′(t) = х″(t). v(t) = x′(t) = - 6t + 6t 2 ; v(2) = - 6∙2 + 6∙4 = 12 (м/с); =0 t=0 или t=1 (с) a(t) = - 6 + 12t; a(2) = -6 + 12∙2 = 18(м/с 2 ). Ответ: v = 12 м/с; t= 1 c; а = 18м/с 2 ." width="640"










 1,5080-1,50780 , то y(x)0 при всех x . Поскольку 30`Y(12) Y(13) ) В силу того, что функция убывает, то решением неравенства является ." width="640"
1,5080-1,50780 , то y(x)0 при всех x . Поскольку 30`Y(12) Y(13) ) В силу того, что функция убывает, то решением неравенства является ." width="640"


![Задание на дом: [3] с. 67-68 1. Решить задачу : Задача. Материальная точка массой 0,01 кг совершает гармонические колебания по закону косинуса с периодом 2сек и начальной фазой равной нулю. Полная энергия колеблющейся точки 1*10 -4 Дж. Найти амплитуду колебаний; написать уравнение данных колебаний; найти наибольшее значение силы, действующей на точку. Изотоп Изотоп Период полураспада Актиний Актиний Период полураспада 10 суток 10 суток Йод Йод Кальций 8 суток 8 суток Кальций 164 суток 164 суток Кобальт Кобальт Магний 5,3 года Магний 5,3 года 10 минут 10 минут Полоний Полоний 138 суток Радий Радий 138 суток 1590 лет 1590 лет Радон Радон 3,82 суток Стронций 3,82 суток Стронций 27 лет 27 лет Уран-235 Уран-235 Уран-238 Уран-238 7,1 10 8 лет 4,5 10 9 лет Фосфор Фосфор 14,3 суток Церий Церий 14,3 суток 285 суток 285 суток 2. Из приведенной таблицы выберите элемент , составьте и решите задачу на применение производной. 3. Составить условие задачи, связанное с вашей специальностью и решить ее, использовав физический смысл производной. 4. Повторить правила дифференцирования и таблицу производных.](https://fsd.videouroki.net/html/2018/12/20/v_5c1b8b1876e5d/img_v99725964_0_39.jpg)










 МЕТОДИЧЕСКАЯ РАЗРАБОТКА открытого урока по дисциплине «Математика» по теме: «Физический смысл производной» (9.7 MB)
МЕТОДИЧЕСКАЯ РАЗРАБОТКА открытого урока по дисциплине «Математика» по теме: «Физический смысл производной» (9.7 MB)
 0
0 1873
1873 167
167 Нравится
0
Нравится
0



