ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
Для самостоятельной работы студентов
По дисциплине: МАТЕМАТИКА
Тема: «Основные понятия и методы математической статистики»
Специальность: 31.02.01 Лечебное дело Курс: 1
Купино
2019
Рассмотрено на заседании предметной цикловой
Методической комиссии по общеобразовательным дисциплинам,
общему гуманитарному и социально-экономическому, математическому и
естественно-научному циклу
Протокол № _____ от «_____» _________20____г.
Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.
Купино
2019 г
Пояснительная записка
Методическое пособие предназначено для самостоятельного изучения теоретических и практических знаний по теме Основные понятия и методы математической статистики, повторения понятий: выборки, относительной частоты, гистограммы, моды, медианы для подготовки к занятиям по этой теме.
Данное пособие рекомендовано для студентов первого курса специальности 31.02.01 Лечебное дело. Пособие содержит определения основных понятий по теме Основные понятия и методы математической статистики, вопросы для самопроверки, образцы решения задач и задачи для самостоятельного решения.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.
Основные понятия и методы математической статистики
Связь математической статистики с теорией вероятностей имеет в разных случаях различный характер. Теория вероятностей изучает не любые массовые явления, а явления случайные и именно «вероятностно случайные», т. е. такие, для которых имеет смысл говорить о соответствующих им распределениях вероятностей. Тем не менее теория вероятностей играет определенную роль и при статистическом изучении массовых явлений любой природы, которые могут не относиться к категории вероятностно случайных. Это осуществляется через основанные на теории вероятностей теорию выборочного метода и теорию ошибок. В этих случаях вероятностным закономерностям подчинены не сами изучаемые явления, а приемы их исследования. Более важную роль играет теория вероятностей при статистическом исследовании вероятностно случайных явлений. Здесь в полной мере находят применение такие основанные на теории вероятностей разделы математической статистики, как проверка статистических гипотез, статистическое оценивание распределений вероятностей и входящих в них параметров и т. д. Область же применения этих более глубоких статистических методов значительно уже, т. к. здесь требуется, чтобы сами изучаемые явления были подчинены достаточно определенным вероятностным закономерностям. Например, статистическое изучение режима турбулентных водных потоков или флюктуаций в радиоприемных устройствах производится на основе теории стационарных случайных процессов. Однако применение той же теории к анализу экономических временных рядов может привести к грубым ошибкам в виду того, что входящее в определение стационарного процесса допущение наличия сохраняющихся в течении длительного времени неизменных распределений вероятностей в этом случае, как правило, совершенно неприемлемо. Вероятностные закономерности получают статистическое выражение (вероятности осуществляются приближенно в виде частот, а математические ожидания – в виде средних) в силу закона больших чисел.
Назовём множество всех изучаемых объектов генеральной совокупностью. Выборочной совокупностью, или кратко выборкой, назовём объекты, отобранные для исследования из генеральной совокупности, а их число n -объёмом выборки.
Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо, чтобы объем выборки был достаточно велик и выборка должна достаточно хорошо представлять пропорции генеральной совокупности. Кратко это требование звучит так: выборка должна быть репрезентативной (представительной), для чего каждый из её объектов должен быть отобран из генеральной совокупности случайным образом, то есть все объекты генеральной совокупности должны иметь одинаковую вероятность попасть в выборку.
К чему может привести несоблюдение правила случайного отбора, показывают многочисленные случаи неправильного проведения предвыборных опросов. Например, в 1936 году перед президентскими выборами в США журнал “Literary Digest” провел опрос 10 миллионов избирателей и предсказал, что Франклин Рузвельт проиграет выборы. Фамилии опрашиваемых избирателей были взяты из телефонных книг. Но в годы депрессии люди, имевшие телефон, не представляли всех избирателей США, выборка оказалась нерепрезентативной и прогноз не оправдался.
Существуют специальные приёмы отбора, обеспечивающие репрезентативность выборки, описание которых можно найти в книгах по статистике. Мы же будем в дальнейшем предполагать, что это требование выполнено и будем обсуждать только вопросы обработки выборочных данных.
Пусть из генеральной совокупности извлечена выборка объёмом n. Случайный выбор элемента рассматривается как независимое наблюдение над величиной x, имеющей некоторое распределение вероятностей. Те значения y1, y2…yn, которые приняла случайная величина x в n наблюдениях, называются ее реализациями. Если эти числа записать не в порядке получения, а в порядке возрастания, то получим упорядоченную выборку x1,x2,…xn, называемую вариационным рядом. Расстояние xn-x1между крайними членами ряда называется размахом вариационного ряда. Выборка и вариационный ряд несут практически одну и ту же информацию, но с вариационным рядом легче работать в силу его упорядоченности. Если изучается величина, имеющая непрерывное распределение вероятностей, то, скорее всего, вариационный ряд не будет содержать повторяющихся значений. Если же изучается дискретная случайная величина, то при достаточно большом объеме выборки в выборке будут повторяющиеся значения. Назовем относительной (эмпирической) частотой значения xiчастоту mi/n, где mi– число совподающих элементов xiв выборке объема n. Разные значения xiназовем вариантами.
Построим по выборке таблицу из двух строк: в верхней строке указаны в порядке возрастания наблюдаемые значения, а в нижней – соответствующие им относительные частоты. Эта таблица называется таблицей статистического распределения выборки.
Для выборки из непрерывного распределения (нет повторяющихся значений) эта таблица будет иметь вид
| Значения xi | x1 | x2 | … | xn |
| Частоты mi/n | 1/n | 1/n | … | 1/n |
Для выборки с повторяющимися значениями таблица выглядит так:
| Значения xi | x1 | x2 | … | xk |
| Частоты mi/n |
|
| … |
|
Соответствие между вариантами, записанными в порядке возрастания, и относительными частотами, задаваемое таблицей статистического распределения выборки, называется статистическим (или эмпирическим) распределением выборки.
Пример . Имея конкретную выборку: 2, 6, 12, 6, 6, 2, 6, 12, 12, 6, 6, 6, 12, 12, 6, 12, 2, 6, 12, 6 (n=20), записать вариационный ряд и дать таблицу статистического распределения выборки.
Решение. Вариационный ряд: 2, 2, 2, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 12, 12, 12, 12, 12, 12, 12.
Статистическое распределение выборки:
| Варианты |
|
|
|
| mi |
|
|
|
| Частоты mi/n | 0,15 | 0,5 | 0,35 |
Контроль: 0,15 + 0,5 + 0,35=1.
При большом числе наблюдений над непрерывной случайной величиной обычно прибегают к группировке данных: область на оси x, куда попали значения x1,…,xn, разбивают на 5-15 интервалов I1, I2,…,Iк (причем длины интервалов не обязательно одинаковы). В качестве “принимаемого” значения при этом будут выступать середины интервалов. Примером самого простого вида группировки может служить округление выборочных значений до ближайшего целого числа. Например, последовательность 0,414, -0,011, 0,666, -1,132 и т.д. обращается в 0, 0, 1, -1,… Аналогично округление может производиться до ближайшего числа, кратного 10 или 100.
Пусть mj- число наблюдений, попавших в интервал Ij, к - число интервалов.
Тогда
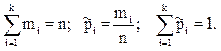 (3.1)
(3.1)
Для наглядного представления статистического распределения пользуются графическим изображением вариационных рядов (полигоном, гистограммой и кумулятой).
В случае дискретного распределения на оси абсцисс откладывают отдельные наблюденные значение х1. Из этих точек хiвосставим перпендикуляры к оси ОХ длиной ![]() либо просто mi. Соединяя отрезками верхние концы соседних перпендикуляров, получим ломаную, называемую полигоном.
либо просто mi. Соединяя отрезками верхние концы соседних перпендикуляров, получим ломаную, называемую полигоном.
Гистограмма строится только для интервального вариационного ряда (группированной выборки). На каждом из интервалов значений как на основании строят прямоугольник с высотой, пропорциональной mi- числу точек выборки в интервале Ii. Если середины верхних сторон соседних прямоугольников соединить отрезками прямых и концы этой ломаной еще соединить с серединами соседних интервалов, частоты которых равны 0, а длина равна длине ближайшего интервала, то получим полигон для группированной выборки.
По выборке легко получить эмпирическую функцию распределения (или функцию распределения выборки, или накопленные частоты). Пусть х - точка оси ОХ, а nx- число точек выборки, попавших левее точки х. Тогда ![]() - доля точек выборки, лежащих левее точки х. Эта частота зависит от х и представляет собой эмпирическую функцию распределения
- доля точек выборки, лежащих левее точки х. Эта частота зависит от х и представляет собой эмпирическую функцию распределения ![]() . Её график - ступенчатая линия. Сглаженное графическое представление этой функции для непрерывной случайной величин даёт кумулята. Покажем это для группированных данных. Имея интервалы группировки I1, I2,...,Ik, подсчитываем в правом конце каждого интервала накопленную частоту и строим перпендикуляр к оси ОХ высотой
. Её график - ступенчатая линия. Сглаженное графическое представление этой функции для непрерывной случайной величин даёт кумулята. Покажем это для группированных данных. Имея интервалы группировки I1, I2,...,Ik, подсчитываем в правом конце каждого интервала накопленную частоту и строим перпендикуляр к оси ОХ высотой ![]() (либо проста высотой nx). Соединяя отрезками прямой верхние концы соседних перпендикуляров, получаем ломаную - кумуляту. Она монотонно поднимается от 0 до 1.
(либо проста высотой nx). Соединяя отрезками прямой верхние концы соседних перпендикуляров, получаем ломаную - кумуляту. Она монотонно поднимается от 0 до 1.
Проще всего показать на конкретном примере, как строятся эти графики (рис. 3.1, 3.2).
Таблица распределения продавцов по выработке
| Выработка продавцов | Число продавцов | В процентах к итогу | Кумулятивная (накопленная) численность | Накопленная частота |
| 80-100 |
|
|
| 0.1 |
| 100-120 |
|
| 15(5+10) | 0.3 |
| 120-140 |
|
| 35(15+20) | 0.7 |
| 140-160 |
|
| 45(35+10) | 0.9 |
| 160-180 |
|
| 50(45+5) |
|
| И т о г о |
|
|
|
|
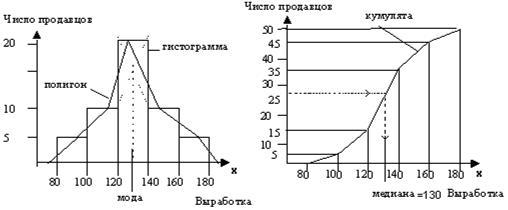
Рис. 3.1 Рис. 3.2
На оси Y могут откладываться не количества, а проценты или проценты, деленные на константу, например частоты. Вид графика от этого не изменится (рис. 3.3, 3.4).
В нашем примере длины интервалов одинаковы. В этом случае при построении гистограммы можно изображать прямоугольники высоты mi. Если длины интервалов разные, то при построении гистограммы это надо учитывать. Например, все интервалы имеют длину 10, кроме крайнего, который имеет длину 50 (весь “хвост” объединен в один интервал). Все попавшие в него данные можно мысленно разбить на 5 одинаковых частей, каждая из которых попала бы в свой интервал длины 10. Следовательно, высота прямоугольника над этим интервалом длины 50 должна браться в 5 раз меньше, чем его m.
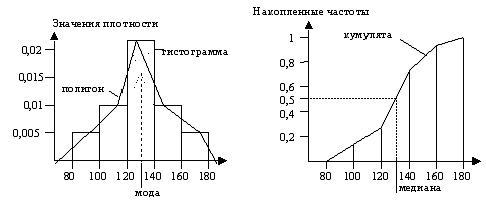
Рис. 3.3 Рис. 3.4
Если строить прямоугольники высоты mi/din, где di– длина интервала Ii, то гистограмма будет изображать эмпирическую плотность. Действительно, плотность вероятности – это вероятность, “приходящаяся в данной точке на единицу измерения”. Вероятность попасть в i-й интервал равна mi/n. Если di- это длина i-го интервала, то вероятность, приходящаяся на единицу измерения, которая и является значением эмпирической плотности внутри этого интервала, равна mi/din (в этом случае вероятность попадания в i-й интервал будет ![]() ). Если строить прямоугольники с такими высотами, то суммарная площадь всех прямоугольников будет равна 1. Таким образом, в случае, когда длины всех интервалов одинаковые, при построении гистограммы по оси y можно откладывать просто значения mi. Если длины интервалов разные, то надо брать за основу mi/di– количества, приходящиеся в этом интервале на единицу интервала. Если высоты прямоугольников сделать равными mi/din, то гистограмма изображает эмпирическую плотность. Такая гистограмма самая удобная в том смысле, что позволяет сравнивать два распределения, имеющие разный объем, и не зависит от способа группировки данных.
). Если строить прямоугольники с такими высотами, то суммарная площадь всех прямоугольников будет равна 1. Таким образом, в случае, когда длины всех интервалов одинаковые, при построении гистограммы по оси y можно откладывать просто значения mi. Если длины интервалов разные, то надо брать за основу mi/di– количества, приходящиеся в этом интервале на единицу интервала. Если высоты прямоугольников сделать равными mi/din, то гистограмма изображает эмпирическую плотность. Такая гистограмма самая удобная в том смысле, что позволяет сравнивать два распределения, имеющие разный объем, и не зависит от способа группировки данных.
Для дискретного вариационного ряда легко находится xi, в котором mi имеет наибольшее значение – это значение, частота которого максимальна. Это значение называется эмпирической модой. Для интервального ряда легко находится интервал, у которого mi максимально. Мода находится внутри него. Для вычисления ее значения пользуются формулой линейной интерполяции. На рис. 3.1 и 3.3 показано, как ее искать графически.
“Накопленные частоты” – это и есть значения эмпирической функции распределения, а кумулята – ее сглаженное графическое изображение.
На графике кумуляты (см. рис. 3.2 и 3.4), или сглаженной эмпирической функции распределения, показана эмпирическая медиана. Медиана – важная характеристика распределения вероятностей. Это такая точка, что половина принимаемых значений лежит слева от нее, а половина справа (это середина распределения). Для дискретного вариационного ряда медиана d ищется по формуле
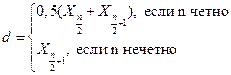 . (3.2)
. (3.2)
Для группированной выборки медиана – это точка, в которой площадь гистограммы делится пополам (в нашем примере – это такая выработка, что у 25 продавцов выработка меньше этого числа, а у 25 больше, и из соображений симметрии видно, что это 130). Если медиана лежит практически в центре области принимаемых значений, то это указывает на то, что у распределения нет сильного перекоса вправо или влево, например, оно симметрично относительно медианы. Сдвиг медианы влево (рис. 3.5) или вправо (рис. 3.7) от центра области принимаемых значений означает больший “вероятностный” удельный вес левой или, соответственно, правой половины распределения.
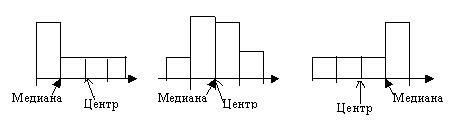
Рис. 3.5 Рис. 3.6 Рис. 3.7
Указав в качестве принимаемых значений середины интервалов группировки, мы строим вероятностную таблицу выборки.
| xi | mi | mi / n | Плотность вероятности | Накопленная частота (эмпирическая функция распределения) |
|
|
| 0,1 | 0,005 | 0,1 |
|
|
| 0,2 | 0,01 | 0,3 = (0,1 + 0,2) |
|
|
| 0,4 | 0,02 | 0,7 = (0,3 + 0,4) |
|
|
| 0,2 | 0,01 | 0,9 = (0,7 + 0,2) |
|
|
| 0,1 | 0,005 | 1 = (0,9 + 0,1) |
| n |
|
|
|
|
Итак, в самом общем случае по выборке построена таблица эмпирического распределения выборки.
| Варианты |
|
| … |
|
| Частоты |
|
| … |
|
Далее задача заключается в том, чтобы по полученному экспериментальному материалу сделать выводы о виде распределения и получить оценки значений его числовых параметров.
Нетрудно заметить полную аналогию между статистическим распределением выборки и законом распределения дискретной случайной величины, но в данном случае вместо возможных значений случайной величины фигурируют варианты, а вместо соответствующих вероятностей – относительные частоты. В силу этой аналогии по известному эмпирическому распределению можно по тем же формулам, что и для дискретного распределения, найти выборочные аналоги математического ожидания и дисперсии или вычислить эмпирическую вероятность события (xx (она равна ![]() , где nx- число наблюдений xi, меньших х), т.е. найти эмпирическую функцию распределения (рис. 3.8), а гистограмму и полигон (рис. 3.9) можно рассматривать как эмпирическую плотность.
, где nx- число наблюдений xi, меньших х), т.е. найти эмпирическую функцию распределения (рис. 3.8), а гистограмму и полигон (рис. 3.9) можно рассматривать как эмпирическую плотность.
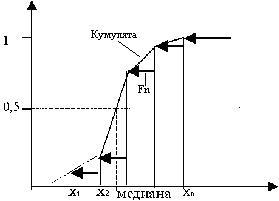
Рис. 3.8. Кумулята и эмпирическая функция распределения
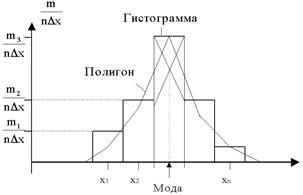
Рис. 3.9. Гистограмма и полигон
Если n увеличивать и, в случае группировки данных, длины интервалов группировки уменьшать, то гистограмма и полигон неограниченно приближаются (на каждом интервале сходятся по вероятности) к кривой плотности вероятности случайной величины (аналогично кумулята сходится по вероятности к теоретической функции распределения).
Поясним коротко, что означает термин “сходится по вероятности”. В курсе анализа изучалось понятие сходимости. Последовательность {an} называется сходящейся к a при n, стремящимся к бесконечности, если разность |an-a| становится при неограниченном росте n как угодно мала.
Пример. По выборке 4, 6, 7, 7, 10, 15, 18 (n=7) найти ![]() и S2.
и S2.
![]() =(4+6+7+7+10+15+18)/7=9,57.
=(4+6+7+7+10+15+18)/7=9,57.
S2=1/7(16+36+49+49+100+225+324)-(9,57)2=114,14-91,58=22,56.
Пример. Найти ![]() и S2по таблице
и S2по таблице
| Варианты |
|
|
|
|
| mi |
|
|
| n=20 |
![]() =(2×3+6×10+12×7)/20=7,5.
=(2×3+6×10+12×7)/20=7,5.
S2=1/20(4×3+36×10+144×49)-(7,5)2=(1/20)×7428-56,25 = 371,4-56,25=315,15.
Эффективное управление здравоохранением невозможно без своевременного получения и анализа полной, достоверной и научно обоснованной статистической информации.
Медицинская статистика (синоним: санитарная статистика, статистика в медицине и здравоохранении, медико-санитарная статистика, статистический метод в медицине и здравоохранении) - отрасль статистики, изучающая явления и процессы в области здоровья населения и здравоохранения.
Основными задачами медицинской статистики являются:
разработка специальных методов исследования массовых процессов и явлений в медицине и здравоохранении;
выявление наиболее существенных закономерностей и тенденций в здоровье населения в целом и в различных его группах (возрастных, половых, профессиональных и др.) во взаимосвязи с конкретными условиями и образом жизни:
изучение и оценка состояния и динамики развития сети, деятельности учреждений здравоохранения и медицинских кадров.
Основой медицинской статистики являются общая теория статистики и математическая статистика. Важная роль в развитии теории и практики медицинской статистики принадлежит математике, кибернетике, информатике, вычислительной технике, автоматизированным системам обработки информации.
При изучении количественной стороны общественных явлений и процессов в области здравоохранения и формирования общественного здоровья медицинская статистика использует специфические методы и приемы, образующие методологию статистического исследования. В методологию статистики входят, в первую очередь, методы статистических наблюдений и математического анализа полученной информации. Для решения конкретных задач статистического изучения разрабатывается методика исследования. Методика является обязательной частью Программы статистического исследования.
Под методологией понимается научно-практическая дисциплина (область знания), изучающая и разрабатывающая принципы, процедуры, методы и средства исследовательской деятельности в выбранной области и нацеленная на решение задач повышения ее результативности и эффективности.
Для осуществления статистического учета в здравоохранении используется официально утвержденный статистический инструментарий в виде статистических форм и инструкций по их заполнению. Для решения каких-либо частных научно-исследовательских и научно-практических задач можно использовать разработанный самостоятельно статистический инструментарий в соответствии с требованиями, предъявляемыми к статистическому исследованию.
Как и во всяком статистическом исследовании, медицинская статистика применяет три последовательные стадии:
Статистическое наблюдение, выражающееся в виде сбора первичного материала, обеспечивающего полноту, достоверность и репрезентативность полученных данных;
Сводка и группировка результатов статистического наблюдения;
Анализ полученных сводных и обобщенных данных и показателей.
В настоящее время практика медицинской статистики основывается на общегосударственной системе учета и отчетности, регламентируемой Федеральным законом "Об официальном статистическом учете и системе государственной статистики в Российской Федерации" от 29.11.2007 N 282-ФЗ.
Действие указанного Федерального закона распространяется на респондентов, субъекты официального статистического учета и пользователей официальной статистической информацией. В нем даны основные понятия в области государственной статистики, к которой относится и медицинская статистика:
официальный статистический учет - деятельность, направленная на проведение в соответствии с официальной статистической методологией федеральных статистических наблюдений и обработку данных, полученных в результате этих наблюдений, и осуществляемая в целях формирования официальной статистической информации;
система государственной статистики - государственная федеральная информационная статистическая система, представляющая собой совокупность позволяющих осуществлять официальный статистический учет первичных статистических данных и административных данных, формируемой на их основе в соответствии с официальной статистической методологией официальной статистической информации и обеспечивающих формирование такой информации информационных технологий и технических средств;
официальная статистическая информация - сводная агрегированная документированная информация о количественной стороне социальных, экономических, демографических, экологических и других общественных процессов в Российской Федерации, формируемая субъектами официального статистического учета в соответствии с официальной статистической методологией;
субъекты официального статистического учета - федеральные органы государственной власти, иные федеральные государственные органы, осуществляющие формирование официальной статистической информации в установленной сфере деятельности в соответствии с законодательством Российской Федерации;
федеральное статистическое наблюдение - сбор первичных статистических данных и административных данных субъектами официального статистического учета;
административные данные - используемая при формировании официальной статистической информации документированная информация, получаемая федеральными органами государственной власти, иными федеральными государственными органами, органами государственной власти субъектов Российской Федерации, иными государственными органами субъектов Российской Федерации, органами местного самоуправления, государственными организациями в связи с осуществлением ими разрешительных, регистрационных, контрольно-надзорных и других административных функций, а также иными организациями, на которые осуществление указанных функций возложено законодательством Российской Федерации;
первичные статистические данные - документированная информация по формам федерального статистического наблюдения, получаемая от респондентов, или информация, документируемая непосредственно в ходе федерального статистического наблюдения;
пользователи официальной статистической информацией - государственные органы, органы местного самоуправления, юридические и физические лица, обращающиеся к системе государственной статистики или субъектам официального статистического учета за получением необходимой им статистической информации и (или) пользующиеся такой информацией.
Принципами официального статистического учета и системы государственной статистики, включая медицинскую статистику, являются:
Полнота, достоверность, научная обоснованность, своевременность предоставления и общедоступность официальной статистической информации (за исключением информации, доступ к которой ограничен федеральными законами);
Применение научно обоснованной официальной статистической методологии, соответствующей международным стандартам и принципам официальной статистики, а также законодательству Российской Федерации, открытость и доступность такой методологии;
Рациональный выбор источников в целях формирования официальной статистической информации для обеспечения ее полноты, достоверности и своевременности предоставления, а также в целях снижения нагрузки на респондентов;
Обеспечение возможности формирования официальной статистической информации по Российской Федерации в целом, по субъектам Российской Федерации, по муниципальным образованиям;
Обеспечение конфиденциальности первичных статистических данных при осуществлении официального статистического учета и их использование в целях формирования официальной статистической информации;
Согласованность действий субъектов официального статистического учета;
Применение единых стандартов при использовании информационных технологий и общероссийских классификаторов технико-экономической и социальной информации для создания и эксплуатации системы государственной статистики в целях ее совместимости с другими государственными информационными системами;
Обеспечение сохранности и безопасности официальной статистической информации, первичных статистических данных и административных данных.
В соответствии со ст. 7 Федерального закона "Об официальном статистическом учете и системе государственной статистики в Российской Федерации" от 29.11.2007 N 282-ФЗ применение официальной статистической методологии является обязательным при формировании официальной статистической информации.
Официальная статистическая методология включает в себя методы сбора, контроля, редактирования, сводки и группировки первичных статистических данных и административных данных, оценки точности официальной статистической информации и ее систематизации.
Официальная статистическая методология формируется субъектами официального статистического учета и утверждается ими по согласованию с федеральными органами исполнительной власти, уполномоченными Правительством РФ.
Материально-технической основой медицинской статистики являются современная вычислительная техника, средства связи, передачи, хранения и отображения информации. Перспективы развития медицинской статистики непосредственно связаны с развитием информационно-коммуникационных технологий.
В медицинской статистике выделяют следующие основные разделы:
общая теория и методы;
статистика здоровья населения;
статистика здравоохранения;
применение методов медицинской статистики в управлении, в клинических, лабораторных, экспериментальных исследованиях.
ОБЩАЯ ТЕОРИЯ И МЕТОДЫ МЕДИЦИНСКОЙ СТАТИСТИКИ включают методологию медико-статистического исследования, т.е. совокупность специфических научных методов и приемов сбора, обработки, анализа и оценки медико-статистической информации. Основными методами статистических исследований являются:
статистическое наблюдение (включая методы планирования и организации статистического исследования);
группировка и сводка материалов наблюдения;
методы первичной статистической обработки данных (вычисление производных величин - средних и относительных, критериев их достоверности);
метод выборочного медико-статистического исследования, включая оценку репрезентативности (представительности) выборочных данных;
методы математико-статистического анализа: статистическая оценка значимости различий сравниваемых показателей, исследование и оценка связей и взаимозависимостей, исследование динамики явлений и процессов, статистическое планирование эксперимента, прогнозирование, многомерный статистический анализ, графический анализ и др.
Медико-статистическое исследование включает пять самостоятельных, но взаимосвязанных этапов:
Планирование исследования (формулировка цели, разработка задач, программы и плана исследования);
Статистическое наблюдение (сбор материала для его последующей статистической обработки);
Статистическая группировка и сводка материалов наблюдения:
Первичная статистическая обработка данных;
Научно-статистический анализ, графическое и литературное оформление результатов исследования. Несмотря на наличие этапов, медико-статистическое исследование представляет собой единое, органически связанное целое, в основе которого лежит целостный, системный подход к изучаемому объекту.
Объектом медико-статистического исследования являются массовые процессы, происходящие среди населения, в сферах оказания медпомощи и проведения санитарно-противоэпидемических мероприятий, анализ которых позволяет вскрыть и охарактеризовать количественно закономерности и особенности здоровья населения в целом и составляющих его групп, развитие и течение болезней среди различных групп населения, деятельность органов и учреждений здравоохранения.
СТАТИСТИКА ЗДОРОВЬЯ НАСЕЛЕНИЯ разрабатывает специфические методы и приемы сбора, обработки, анализа и оценки медико-статистической информации о процессах и явлениях, характеризующих состояние и динамику здоровья населения, его качественно однородных групп в связи с конкретными социальными, экономическими и природными условиями: демографические процессы, физическое развитие, заболеваемость населения, временная нетрудоспособность, инвалидность и др.
СТАТИСТИКА ЗДРАВООХРАНЕНИЯ создает специфические методы и приемы сбора, обработки, передачи, хранения, анализа и оценки информации о состоянии и изменениях сети учреждений и органов здравоохранения, их деятельности, кадров здравоохранения, медико-санитарного имущества и др.
Важное место в медицинские статистики нанимают фактические медико-статистические данные, регулярно собираемые, обрабатываемые, анализируемые и используемые в повседневной оперативной работе учреждениями и органами здравоохранения, а также направляемые в строго установленном порядке по подчиненности в виде специальных документов государственной медицинской отчетности. С этой целью в системе здравоохранения создана медико-статистическая служба, низовым звеном которой являются кабинеты медицинского учета и статистики медицинских учреждений. Главной задачей этой службы является обеспечение учреждений и органов здравоохранения достоверной, полной и своевременной информацией.
Одним из важных направлений медицинской статистики служит разработка научно обоснованных критериев (показателей) состояния здоровья населения и деятельности учреждений и органов здравоохранения, а также систем таких критериев (показателей), которые могут быть использованы в процессе управленческой работы с целью объективной оценки складывающихся конкретных ситуаций (врачебной деятельности, деятельности конкретных учреждений, их групп и т.д.), их планирования и прогнозирования.
Важными медико-статистическими показателями являются показатели здоровья населения (смертность, заболеваемость и др.), показатели, характеризующие работу лечебно-профилактических учреждений, санитарно-профилактических, аптечных и других медицинских учреждений (подразделений).
Медико-статистические показатели периодически пересматриваются в соответствии с новыми задачами здравоохранения, развитием медицинской науки и практики, технической оснащенности служб здравоохранения.
Статистическая совокупность – группа, состоящая из множества относительно однородных элементов (единиц наблюдения). Например, группа оперированных, население на участке, больные стационара, новорожденные на данном участке, пациенты поликлиники, больные на дому и т.д.
Единица наблюдения –каждое отдельное явление, подлежащее учету, наделенное признаками сходства.
В большинстве социально- гигиенических исследований учитываемыми признаками является: пол, возраст, семейное положение, уровень образования, доход и размеры жилплощади на одного человека, масса тела, рост, длительность пребывания в стационаре и др. (количественные признаки, выраженные числом).
Различают так же факторные и результативные признаки в зависимости от характера влияния: какой признак на какой влияет (возраст – факторный признак, а рост - результативный).
Методами обработки медико – биолоических исследований являются методы расчета средних, относительных величин.
Одной из основных областей применения математической статистики в медицине является обоснование выводов, вытекающих из сравнения статистических показателей. Основным вопросом при этом является суждение о том, в какой мере обнаружения при исследовании разность между выборочными показателями может свидетельствовать о существенном, неслучайном различии генеральных совокупностей.
В статистике широкое применение нашла нулевая гипотеза Н0. Так если одна выборка извлечена из генеральной совокупности с параметрами М(х) и σх, а другая – из совокупностей с параметрами М(Y) и σу, то нулевая гипотеза исходит из того, что М(х) – М(Y) = 0 и σх - σу = 0 (отсюда и название гипотезы – нулевая).
Противоположная нулевой – конкурирующая гипотеза Н1 – исходит из предположения, что М(х) – М(Y) ≠ 0 и σх - σу≠ 0.
Для проверки принятой гипотезы используют величины, функции распределения которых известны и сведены в специальные таблицы. Принимают три уровня значимости, или вероятности ошибки, допускаемой при проверке статистических гипотез:
5% -ный (вероятность ошибочной оценки Р = 0,05)
1% -ный (Р = 0,01)
0,1% ный (Р = 0,001).
В биологических исследованиях часто считают достаточным 5% -ный уровень значимости. При этом гипотезу Н0 не отвергают, если вероятность ошибочности оценки относительно принятой гипотезы превышает 5%.
Если же эта вероятность меньше 5 %, то принятую гипотезу следует отвергнуть на взятом уровне. Ошибка при этом возможна не более, чем в 5 % случаев, т.е. она маловероятна. При более ответственных исследованиях уровень значимости может быть уменьшен до 1 % или даже 0,1 %.
В области биометрии применяются два вида статистических критериев.
Параметрические, построенные на основании параметров данной совокупности и представляющие функции этих параметров.
Непараметрические- представляющие собой функции, зависящие непосредственно от варианта данной совокупности с их частотами.
Обработка медико-биологических данных
Внедрение в повседневную медицинскую и биологическую практику таких областей современной науки и техники: как теория управления, математическое моделирование, вычислительная техника, стимулирует разработку разнообразных методов и средств съема и регистрации экспериментальной информации, способствующая качественному улучшение результатов анализа медико-биологических наблюдений, позволяет синтезировать новые методы машинной диагностики и прогнозирования состояния биологического организма. Использование современной техники инструментальных исследований целостного организма его систем и звеньев в сочетании с математическими и машинными (автоматическими и автоматизированными) методами анализа экспериментальной информации способствует решение основных задач, стоящих перед здравоохранением. При этом наряду с улучшением процессов диагностики и лечения становится актуальной задача расширения массового медицинского обследования населения с целью своевременного выявления трудноизлечимых заболеваний, а также организация по медицинским и психофизиологическим показателям профессионального отбора работников для различной производственной деятельности.
Повышенный интерес к автоматизации получения, анализа биомедицинской информации и принятия решений обусловлен рядом причин. Одна из них заключается во внутреннем противоречии самой тенденции автоматизации медико-биологических исследований. Эта тенденция обусловлена стремлением, увеличить объем информации о состоянии биологического объекта, сделать эту информацию количественной, объективной, точной. Вместе с тем, увеличение объема регистрируемой информации существенно усложняет ее анализ, приводит к увеличению времени на диагностирование состояния биообъекта, вынуждает специалистов заниматься непроизводительным, рутинным трудом. Рядом исследователей отмечалось, что уже в настоящее время рутинная обработка информации занимает более 55%времени квалифицированных врачей и среднего медицинского персонала. Поэтому основным движущим фактором автоматизации обработки медико-биологической информации является то обстоятельство, что без автоматизации нельзя повысить качество диагностики состояния биологического объекта.
Несомненным также является обстоятельство, что автоматизация анализа медико-биологической информации (вплоть до постановки диагноза и прогнозирования состояния объекта наблюдения) позволит формализовать процедуру обработки экспериментальной информации, исключает при принятии решения элементы случайности и субъективности, связанные о индивидуальной квалификацией и опытом врача и исследователя.
Задача автоматизации обработки экспериментальных данных и предъявления их исследователю для принятия решения связана с фундаментальными проблемами распознавания образов.
Автоматизированный медико-биологический эксперимент
Применение ЭВМ (особенно ПК) для обработки медико-биологических данных оказывается наиболее эффективным в автоматизированном эксперименте (рис. 6.1).
С помощью датчиков, которые реагируют на изменение того или иного параметра путем преобразования в электрический сигнал, разнообразные характеристики объекта исследования приводятся к единому физическому носителю, причем датчики отводят информацию не только от объекта исследования, но и от среды, в которой объект находится, что необходимо для проведения исследований в определенных условиях. В некоторых случаях должна быть предусмотрена возможность изменения этих условий в соответствии с заданным планом, — такой эксперимент называется управляемым. Такой подход является перспективным, поскольку открывает принципиально новые методические возможности. Однако, пока в большинстве случаев исследователю приходится ограничиться неуправляемым экспериментом, оставаясь в роли пассивного наблюдателя.
Система передачи данных выполняет преобразование информации, которое необходимо для осуществления дистанционной передачи (кодировка, уплотнение, преобразование типа модуляция-демодуляция и т.п.). Качественные показатели, которые не могут быть автоматически измерены, вводятся специалистом.
Отметим два магистральных направления при обработке медико-биологических данных:
1.Замена врача вычислительным комплексом — создание интеллектуальных систем. Это направление выражается в разработке такого программного обеспечения, которое позволяло бы ЭВМ по входным медико-биологическим данным поставить диагноз. Такие системы могут быть использоваться для профилактического осмотра населения с принятием решения типа «болен - здоров». Делаются и более сложные попытки дифференцирования заболеваний, характеризующихся большим набором признаков, имеющих различную вероятность появления в диагностируемых заболеваниях.
2.ЭВМ выполняет формализуемую, трудоемкую работу по обработке и представление полученных данных, а на врача (исследователя) возлагается творческий процесс диагностики — интерактивные системы. Обработка информации занимает, по оценке специалистов, 20 — 30 % рабочего времени. Такие системы дают неожиданные возможности как по обработке информации, так и по представлению данных.
Использование ЭВМ для обработки медико-биологических данных исходит из того, что никакая, даже самая совершенная система не может, да и не должна заменить врача в ходе диагностического или лечебного процесса. Именно за врачом остается решающее слово при окончательной интерпретации результатов автоматизированной обработки данных и принятия решений о проведении тех или иных лечебных мероприятий. Автоматизированные системы обработки данных должны обеспечить наибольшее раскрытие творческого потенциала врача.
Естественное движение населения — это изменение численности населения в результате рождений и смертей.
Изучение естественного движения осуществляется с помощью абсолютных и относительных показателей.
Абсолютные показатели
1. Число родившихся за период (Р)
2. Число умерших за период (У)
3. Естественный прирост (убыль) населения, который определяется как разность между числом родившихся и умерших за период: ЕП = Р — У
Относительные показатели
Среди показателей движения населения выделяют: коэффициент рождаемости, коэффициент смертности, коэффициент естественного прироста и коэффициент жизненности.
Все коэффициенты, кроме коэффициента жизненности, рассчитываются в промилле, т. е. на 1000 человек населения, а коэффициент жизненности определяется в процентах (т. е. на 100 человек населения).
Общий коэффициент рождаемости
Показывает, сколько человек рождается в течение календарного года в среднем на каждую 1000 человек наличного населения
Общий коэффициент смертности
Показывает, сколько человек умирает в течение календарного года в среднем на каждую 1000 человек наличного населения и определяется по формуле:
Коэффициент смертности в России (число умерших на 1000 человек населения) с 11,2 промиллей в 1990 году увеличился до 15,2 в 2006 году, а коэффициент рождаемости снизился соответственно с 13,4 до 10,4 промиллей в 2006 году.
Высокая смертность связана с устойчивой тенденцией роста заболеваемости. В сравнении с развитыми странаминаши недуги переходят в хроническую форму на 15-20 лет. Отсюда и массовая инвалидизация и преждевременная смертность.
Статистика неутешительная: большая часть населения ведет нездоровый образ жизни: неправильное питание, потребление плохой воды, массовое пренебрежение физической культурой, пьянство и алкоголизм, курение, наркотики и прочее. Доступность качественной медицинской помощи — на недопустимо низком уровне. Чтобы попасть на прием ко многим врачам, населению надо перетерпеть большие очереди. Государственных средств в бюджетах всех уровней значительно ниже, чем в развитых странах мира, всего 3-4 % от ВВП, при норме — 7 %.
Бедность в сознании людей все более ассоциируется с неспособностью получать необходимую медицинскую помощь. О каком уровне человеческого потенциала, работоспособности человека и эффективности его деятельности может идти речь, если в «дежурное» его состояние превратился стресс. За годы реформ стрессы стали сопровождать нас каждый день: значительная инфляция, дороговизна товаров, задержки зарплаты, потеря работы и т.д.
Больше всего разрушает здоровье наемных работников неквалифицированный менеджмент. Без глубоких исследований известно, что практически половина людей приходит на работу с различными недомоганиями, нестабильным давлением, сердечной недостаточностью. Когда работодатели ставят работнику задачу достичь каких-то результатов, он часто в прямом и переносном смысле «потеет», «выделяет» и «нагревается». Всё это расшатывает нервную систему, возникают различные серьёзные заболевания.
Демографический «крест» и постоянные стрессы влияют на развитие экономики и качество жизни населения.
Коэффициент естественного прироста
Показывает величину естественного прироста (убыли) населения в течение календарного года в среднем на 1000 человек наличного населения и вычисляется двумя способами:
Коэффициент жизненности
Показывает соотношение между рождаемостью и смертностью, характеризует воспроизводство населения. Если Коэффициент жизненности меньше 100%, то население региона вымирает, если выше 100%, то численность населения увеличивается. Этот коэффициент определяется двумя способами:
Специальные показатели
В демографической статистике кроме общих коэффициентов рассчитывают также специальные показатели:
Коэффициент брачности
Показывает, сколько браков приходится на 1000 человек в течение календарного года.
К брачности = (число лиц, вступивших в брак / среднегодовая численность населения)*1000
Коэффициент разводимости
Показывает, сколько разводов приходится на каждую тысячу населения в течение календарного года. Например, в 2000 г. в России на каждую 1000 человек населения приходилось 6,2 браков и 4,3 разводов.
К разводимости = (число лиц, разведенных в году / среднегодовая численность населения)*1000
Коэффициент младенческой смерти
Вычисляется как сумма двух составляющих (в промилле).
Первая — отношение числа умерших в возрасте до одного года из поколения, родившегося в этом году, для которого вычисляется коэффициент, к общему числу родившихся в этом году.
Вторая — отношение числа умерших в возрасте до одного года из поколения, родившегося в предшествующем году, к общему числу родившихся в предыдущем году.
В 2000 г. этот показатель составлял в нашей стране 15,3‰.
К младенческой смертности = (число умерших детей в возрасте до 1 года / число родившихся живыми за год)*1000
Возрастной коэффициент рождаемости
Показывает число родившихся в среднем на 1000 женщин каждой возрастной группы
Специальный коэффициент рождаемости (плодовитости)
Показывает, какое количество рождений приходится в среднем на 1000 женщин в возрасте от 15 до 49 лет.
Возрастной коэффициент смертности
Показывает среднее число умерших на 1000 человек населения данной возрастной группы.
Суммарный коэффициент рождаемости
Зависит от возрастного состава населения и показывает, сколько в среднем детей родила бы одна женщина на протяжении её жизни при сохранении в каждом возрасте существующего уровня рождаемости.
Ожидаемая продолжительность жизни при рождении
Один из важнейших показателей, рассчитываемых в международной демографической статистике. Он показывает число лет, которое в среднем предстояло бы прожить человеку из поколения родившихся при условии, что на протяжении всей жизни этого поколения половозрастная смертность останется на уровне того года, для которого вычислен этот показатель. Он рассчитывается с помощью составления и анализа таблиц смертности, в которых для каждого поколения вычисляется численность выживших и умерших.
Ожидаемая продолжительность жизни при рождении в 2000 г. составляла в России 65,3 лет, в том числе для мужчин — 59,0; для женщин — 72,2 лет.
Коэффициент эффективности воспроизводства населения
Показывает долю естественного прироста в общем обороте населения
— число родившихся за год
— число умерших за год
Расчет демографических показателей (рождаемость, смертность, естественный прирост).
1.Возрастная структура населения определяется по следующей формуле (1.1):
В= число лиц определенной возрастной группы : среднегодовая численность населения х100% (1.1)
где В — доля лиц соответствующей возрастной группы.
2. Половая структура населения рассчитывается по формуле (1.2):
П= число лиц определенного пола : среднегодовая численность населения х100% (1.2)
где П — доля лиц соответствующего пола.
3. Общий показатель рождаемости (рождаемость) представляет собой общее число родившихся живыми в течение года детей, приходящееся на 1000 населения, и рассчитывается по формуле (1.3):
ОПР = общее число родившихся в течение года: среднегодовая численность населения x1000 (1.3)
где ОПР — общий коэффициент рождаемости (рождаемость).
4.Коэффициент плодовитости рассчитывают по следующей формуле (1.4):
П = общее число родившихся в течение года : среднегодовая численность женского населения фертильного возраста (15-49 лет) х1000 (1.4)
где П — общий коэффициент плодовитости.
5. Общий показатель смертности рассчитывается по формуле (1.5):
ОПС = общее число умерших в течение года : среднегодовая численность населения х1000 (1.5)
где ОПС - общий показатель смертности.
6.Показатель естественного прироста, определяемый разностью между показателями рождаемости и общей смертности (формула 1.6).
ЕП = ОПР-ОПС, (1.6)
где ЕП — показатель естественного прироста,
ОПР — общий коэффициент рождаемости (рождаемость),
ОПС — общий показатель смертности.
Воспользовавшись вышеприведенными формулами, можно определить основные демографические показатели на территории области, города, в районе обслуживания поликлиники или на конкретном терапевтическом участке.
Пример. Среднегодовая численность населения, находящегося под наблюдением семейного врача, составляет 1500 человек, из них в возрасте до 14 лет — 225 человек, лиц старше 50лет — 300, женщин — 780, в течение года в семьях родилось 15 детей, умерло 18 человек. Таким образом, используя формулы 1.1-1.6, можно определить:
* возрастной тип населения;
* рождаемость;
* смертность;
* естественный прирост населения.
1)определение возрастного типа населения:
доля лиц до 14 лет =225:1500х100% = 15 %
доля лиц старше 50 лет =300 :1500 х100% = 20 %
2)структура населения по полу:
доля женщин = 780:1500 х100% =52%;
доля мужчин =100 % - 52% =48%
3) общий показатель рождаемости:
ОПР =15:1500 х 100% =10 %
4)общий показатель смертности:
ОПС = 18:1500 х 100% = 12%
5)естественный прирост:
10-12=-2 (%)
Таким образом, характеризуя демографическую ситуацию среди семей, находящихся под наблюдением, можно отметить, что возрастной тип населения является регрессивным с преобладанием женского населения, рождаемость находится на низком уровне, смертность — на среднем уровне, естественный прирост населения отрицателен, то есть можно говорить о противоестественной убыли населения. На основании этих данных можно сделать вывод о необходимости усиления деятельности медицинской сестры по планированию семьи, следует также уделить внимание охране здоровья женщин и лиц пожилого возраста.
Вопросы для самопроверки
Сформулируйте определение статистики (ТЗ 50)
Перечислите задачи статистики (ТЗ 51)
Сформулируйте определение статистическая совокупность (ТЗ 52)
Перечислите учетные признаки (ТЗ 53)
Перечислите этапы статистического исследования (ТЗ 54)
Сформулируйте краткую характеристику первого этапа статистического исследования (ТЗ 55)
Сформулируйте краткую характеристику второго этапа статистического исследования (ТЗ 56)
Сформулируйте краткую характеристику третьего этапа статистического исследования (ТЗ 57)
Сформулируйте краткую характеристику четвертого этапа статистического исследования (ТЗ 58)
Сформулируйте краткую характеристику пятого этапа статистического исследования (ТЗ 59)
Сформулируйте определение полигона (ТЗ 60)
Сформулируйте определение гистограммы (ТЗ 61)
Перечислите основные показатели выборки (ТЗ 62)
Сформулируйте определение выборки или выборочной совокупности данных (ТЗ 63)
Сформулируйте определение объема выборки (ТЗ 64)
Сформулируйте определение репрезентативности выборки (ТЗ 65)
Сформулируйте определение показателя или параметра (ТЗ 66)
Сформулируйте определение оценки показателя или параметра (ТЗ 67)
Задачи для самостоятельного решения
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 146
Текст задания: Вычислить р(х4), р(2≤х≤4), математическое ожидание, дисперсию и среднеквадратическое отклонение, если закон распределения случайной величины задан таблично.
| xi | 1 | 2 | 3 | 4 | 5 |
| pi | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 147
Текст задания: Вычислить среднее время ожидания автобуса и дисперсию., если время ожидания автобуса (х) измеряется в минутах и распределено равномерно на отрезке [0, 30].
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 148
Текст задания: Вычислить размах выборки 1, 10, -2, 1,0, 1, 10, 7, -2, 10, 10, 7.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 149
Текст задания: Вычислить объем, выборочное распределение и размах выборки 3,8,-1,3, 0, 5,3,-1,3, 5. Построить полигон частот.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 150
Текст задания: При измерении напряжения в электросети получена следующая выборка:
218, 221, 215, 225, 225, 217, 224, 220, 220, 219, 221, 219, 222, 227, 218, 220, 223, 230, 223, 216, 224, 227, 220, 222 (данные выражены в вольтах). Построить гистограмму частот, если число частичных промежутков равно 5.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 151
Текст задания: На основании данных о средней заработной плате работников в области в тыс. руб., которые помещены в интервальный вариационный ряд в таблицу, построить гистограмму распределения частот зарплаты работников:
| Заработная плата | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 |
| Число Работников |
|
|
|
|
|
|
Критерии оценивания задач:
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 146
Текст задания: Вычислить р(х4), р(2≤х≤4), математическое ожидание, дисперсию и среднеквадратическое отклонение, если закон распределения случайной величины задан таблично.
|
| xi | 1 | 2 | 3 | 4 | 5 |
| |
|---|---|---|---|---|---|---|---|---|
|
| pi | 0,1 | 0,2 | 0,4 | 0,2 | 0,1 |
| |
| Критерии | Оценка (да-1\нет 0) | |||||||
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
| |||||||
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: р(х
р(х4)=0,1;
р(2≤х≤4)=0,2+0,4+0,2=0,8;
М(х)=1*0,1+2*0,2+3*0,4+4*0,2+5*0,1=3;
D(x)=12*0,1+22*0,2+32*0,4+42*0,2+52*0,1-32=1,2
σ(x)= =1,095
Ответ: р(х
р(х4)=0,1;
р(2≤х≤4)= =0,8;
М(х) =3;
D(x) =1,2
σ(x)=1,095
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 147
Текст задания: Вычислить среднее время ожидания автобуса и дисперсию., если время ожидания автобуса (х) измеряется в минутах и распределено равномерно на отрезке [0, 30].
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон:
Ответ: М(х)=15 D(х) = 75
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 148
Текст задания: Вычислить размах выборки 1, 10, -2, 1,0, 1, 10, 7, -2, 10, 10, 7.
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: записав заданную выборку в виде неубывающей последовательности, получим вариационный ряд
-2,-2,0, 1, 1, 1,7,7, 10, 10, 10, 10.
Размах данной выборки равен 10 - (-2) =12.
Ответ: 12
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 149
Текст задания: Вычислить объем, выборочное распределение и размах выборки 3,8,-1,3, 0, 5,3,-1,3, 5 Построить полигон частот.
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: Объем выборки n = 10, ее размах равен 8 - (-1) = 9. Записав значения выборки в виде неубывающей последовательности получим вариационный ряд
-1,-1,0, 3,3, 3,3, 5, 5, 8.
Статистический ряд можно записать в виде последовательности пар чисел - (-1;2), (0;1), (3;4), 5;2), (8;1)
Для контроля находим сумму частот: 2+ 1 +4 + 2+ 1 = 10 и убеждаемся в том, что она равна объему выборки.
Вычислив относительные частоты, найдем выборочное распределение:
| -1 |
|
|
|
|
|
|
|
|
|
|
Для контроля убеждаемся в том, что сумма относительных частот равна единице:
+
+
+
+
=1.
Полигон частот для заданной выборки имеет вид:
Ответ: 10, 9,
| -1 |
|
|
|
|
|
|
|
|
|
|
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 150
Текст задания: При измерении напряжения в электросети получена следующая выборка:
218, 221, 215, 225, 225, 217,
224, 220, 220, 219, 221, 219,
222, 227, 218, 220, 223, 230,
223, 216, 224, 227, 220, 222
(данные выражены в вольтах). Построить гистограмму частот, если число частичных промежутков равно 5.
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: Наименьшее значение выборки равно 215, наибольшее — 230.
Находим длину частичных промежутков . Подсчитываем с учетом кратности число значений выборки, попавших в каждый промежуток.
Для первого промежутка [215; 218) это число равно 3, для второго [218; 221) оно равно 8, для третьего [221; 224) — 6, для четвертого [224; 227) — 5, для пятого [227; 230] — 2. Следовательно, высоты прямоугольников (слева направо), образующих гистограмму, равны По полученным данным строим гистограмму
Д ля контроля убеждаемся в том, что площадь гистограммы равна объему выборки:
Ответ: рисунок
Условия выполнения задания
1. Место выполнения задания в учебной аудитории.
2. Максимальное время выполнения задания: 5 мин.
3. Вы можете воспользоваться лекциями, учебником, калькулятором.
Разработчик: Тюменцева О. Н.
ПРАКТИЧЕСКОЕ ЗАДАНИЕ (ПЗ)№ 151
Текст задания: На основании данных о средней заработной плате работников в области в тыс. руб., которые помещены в интервальный вариационный ряд в таблицу, построить гистограмму распределения частот зарплаты работников:
| Заработная плата | 1-3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 |
| Число Работников |
|
|
|
|
|
|
| Критерии | Оценка (да-1\нет 0) |
| Назван верно математический метод для решения профессиональных задач Найдено правильное решение прикладных задач Представлен верный ответ при решении прикладной задачи в области профессиональной деятельности (всего 30 вариантов для разных методов и видов профессиональных задач) |
|
При дихотомической системе оценивания критерием оценки выступает правило: за правильный ответ (соответствующий эталонному – показателю) выставляется 1 балл, за неправильный ответ (несоответствующий эталонному – показателю) выставляется 0 баллов.
Оценивание осуществляется по критериям:
«5» - 3 балла
«4» - 2 балла
«3» - 1 балл
«2» - 0 баллов
Эталон: При построении гистограммы по оси абсцисс откладываются значения изучаемого признака (границы интервалов), а по оси у – соответствующие частоты, в том случае, если интервалы одинаковой величины. Получим гистограмму:
Гистограмма распределения частот зарплаты работников
Ответ: рисунок

 Получите свидетельство
Получите свидетельство Вход
Вход












 Методическая разработка для самостоятельной работы студентов по теме Основные понятия и методы теории вероятностей (388.5 KB)
Методическая разработка для самостоятельной работы студентов по теме Основные понятия и методы теории вероятностей (388.5 KB)
 0
0 193
193 6
6 Нравится
0
Нравится
0


