Методическая разработка для 8 класса по теме : " Теорема Пифагора"

Теорема Пифагора

Пифагор

• Родился на о. Самос в Эгейском море
• Во время путешествия в возрасте 18–20 лет посетил математика Фалеса
• В южноиталийском г. Кротоне основал пифагорейский союз (школу)
• В школе считали, что в основе всего лежат числа и гармония, но все в математике нужно доказывать
• После 30-летнего существования союза Пифагор с учениками уехал в г. Тарент, а потом в г. Месапонт, где и погиб от рук солдата почти 95-летний Пифагор

Теорема Пифагора (Формулировка 1)

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

О треугольнике со сторонами 3, 4, 5 (   )– говорится в папирусе (2000 г. до н. э.). Соотношение между сторонами прямоугольного треугольника обнаружили и на вавилонских клинописных табличках, и в древнекитайских и древнеиндийских трактатах.

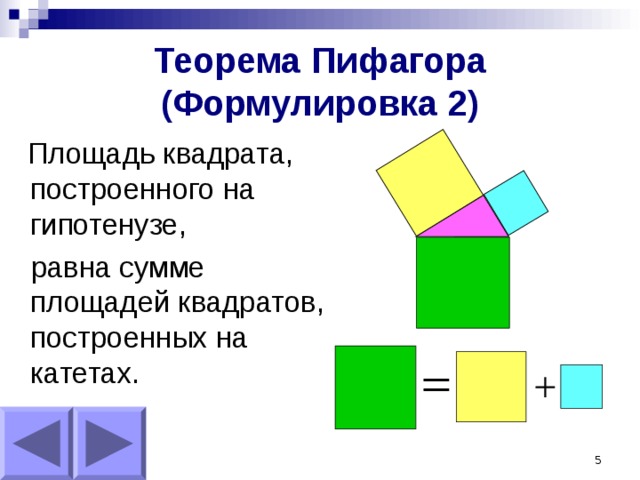
Теорема Пифагора (Формулировка 2)

Площадь квадрата, построенного на гипотенузе,

равна сумме площадей квадратов, построенных на катетах.

• Теорема не теряет смысла, если квадраты заменить любыми другими правильными многоугольниками или полукругами.

5

• Если на сторонах треугольника построены полукруги по одну сторону гипотенузы, то площадь полученных луночек равна площади данного треугольника.

5

Доказательство

• Сумма площади полукругов, построенных на катетах, равна площади полукруга, построенного на гипотенузе, и из них вычитаются одни и те же сектора (выделенные оранжевым цветом)

5

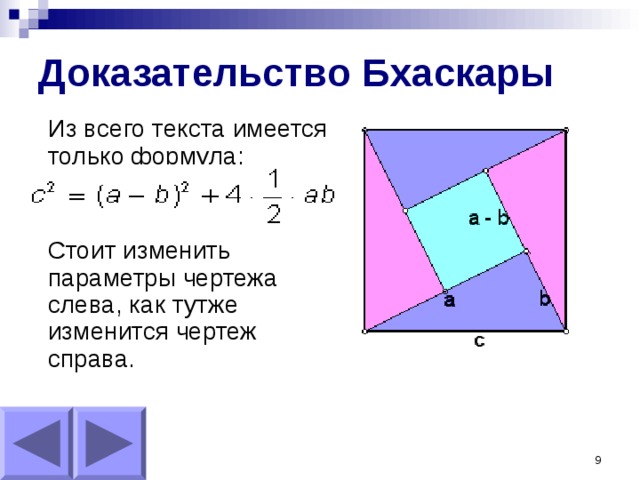
Доказательство Бхаскары

Из всего текста имеется только формула:

Стоит изменить параметры чертежа слева, как тутже изменится чертеж справа.

Шарнирное доказательство

• Фигура, состоящая из двух малых квадратов, разрезается всего на три части, после перекладывания которых образуется большой квадрат.

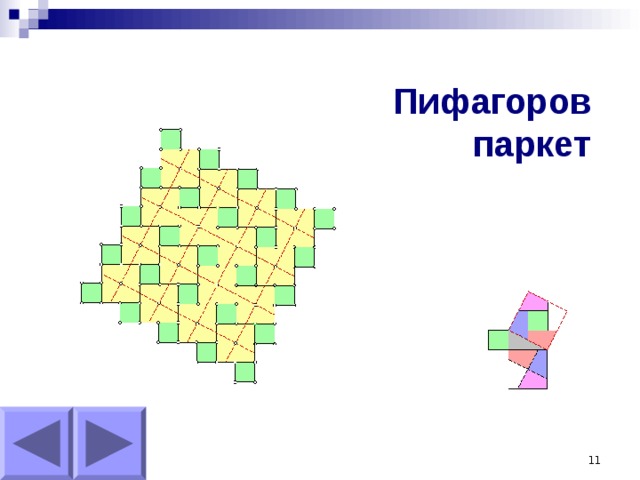
Пифагоров паркет

Теорема Пифагора по Евклиду

• Равенство площадей устанавливается с помощью некоторого преобразования.
• Это доказательство нетрудно обобщить на произвольный треугольник, т.к. в его основе лежит теорема косинусов:

• Прямоугольные треугольники, длины сторон которых – целые числа, называются Пифагоровыми
• Прямоугольный треугольник со сторонами 3, 4, 5 называется Египетским
• тройки ( a, b, c ) натуральных чисел, удовлетворяющие уравнению - Пифагоровыми