МЕТОДИКА ИЗУЧЕНИЯ ТЕМЫ «РАВНОМЕРНОЕ ДВИЖЕНИЕ ТОЧКИ ПО ОКРУЖНОСТИ» В ШКОЛЬНОМ КУРСЕ ФИЗИКИ.
В.В.АБАЛЬМАСОВ
МОУ ГИМНАЗИЯ №1, Г.БАЛАШОВ
Аннотация: предложен наиболее понятный для школьников вывод формулы для нахождения центростремительного ускорения.
Движение тела по окружности или дуге окружности довольно часто встречается в природе и технике. Любое криволинейное движение можно представить приближенно как движение по дугам некоторых окружностей. Можно привести много примеров движений тел, траекторией которых является окружность (движение самолета, описывающего «мертвую петлю», людей на карусели, мотоциклов на поворотах дороги и т. д.). Знакомство с таким движением имеет большое значение. Движение тела по окружности характеризуется центростремительным ускорением. Формула для определения центростремительного ускорения сыграла существенную роль в открытии закона всемирного тяготения. Закон же всемирного тяготения лежит в основе небесной механики. С помощью этого закона с огромной точностью определяются положения небесных тел на небесном своде на многие десятки лет вперед и вычисляются их траектории. Закон всемирного тяготения применяется также в расчетах движения искусственных спутников Земли и межпланетных автоматических аппаратов. Формула для нахождения центростремительного ускорения используется для вычисления первой космической скорости. Зная центростремительное ускорение, рассчитывается центростремительная и центробежная силы. Эти силы находят широкое применение в технике: центрифуги, центробежные регуляторы паровой машины, бельевая сушка, газотурбинные двигатели. Без знания основных законов вращательного движения совершенно невозможно понять ни закономерностей движения планет и космических аппаратов, ни законов микромира. Поэтому при изучении темы «Равномерное движение точки по окружности» очень важно сформулировать у учащихся наиболее наглядные и полные представления о центростремительном ускорении. Однако при непосредственном рассмотрении данной темы в школьном курсе физики вывод формулы центростремительного ускорения для школьников оказывается затруднительным. А представления о силах, действующих на тело при его движении по криволинейной траектории, до сих пор остаются одними из самых неоднозначных вопросов в физике.
Формула центростремительного ускорения 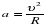 имеет свою историю возникновения. Первым, кто получил зависимость центростремительного ускорения от квадрата скорости и радиуса окружности, считается голландский физик и математик Христиан Гюйгенс (1629-1695гг.). В мемуарах «О центробежной силе» (этот трактат был опубликован только после смерти Гюйгенса в 1703г.) приведены 17 предположений с доказательствами. Предположения 2 и 3 доказывают для случая равных масс 1 и 2 следующие пропорции: если
имеет свою историю возникновения. Первым, кто получил зависимость центростремительного ускорения от квадрата скорости и радиуса окружности, считается голландский физик и математик Христиан Гюйгенс (1629-1695гг.). В мемуарах «О центробежной силе» (этот трактат был опубликован только после смерти Гюйгенса в 1703г.) приведены 17 предположений с доказательствами. Предположения 2 и 3 доказывают для случая равных масс 1 и 2 следующие пропорции: если 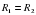 , то
, то 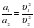 и если
и если 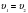 , то
, то 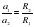 . Из этих теорем можно вывести общий случай, т.е. прямую пропорциональность центростремительного ускорения квадрату скорости и обратную пропорциональность радиусу
. Из этих теорем можно вывести общий случай, т.е. прямую пропорциональность центростремительного ускорения квадрату скорости и обратную пропорциональность радиусу 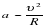 .
.
В школьных учебниках физики для вывода формулы центростремительного ускорения чаще всего используется способ, основанный на предельном переходе. Однако учащиеся 10 классов знакомятся с понятием «предел» на уроках математики позднее, чем рассматривается в механике тема «равномерное движение тела по окружности». Кроме того, при доказательстве формулы 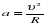 рассматриваются треугольники ОММ1 и М1АВ, которые подобны как равнобедренные с равными углами при вершинах (рис.1). Причем угол МОМ1 равен углу ВАМ1, т.к. соответствующие стороны перпендикулярны. Но учащиеся малознакомы с этой теоремой. В школьном курсе геометрии не акцентируется внимание на теорему, показывающую равенство углов, если соответствующие стороны перпендикулярны.
рассматриваются треугольники ОММ1 и М1АВ, которые подобны как равнобедренные с равными углами при вершинах (рис.1). Причем угол МОМ1 равен углу ВАМ1, т.к. соответствующие стороны перпендикулярны. Но учащиеся малознакомы с этой теоремой. В школьном курсе геометрии не акцентируется внимание на теорему, показывающую равенство углов, если соответствующие стороны перпендикулярны.
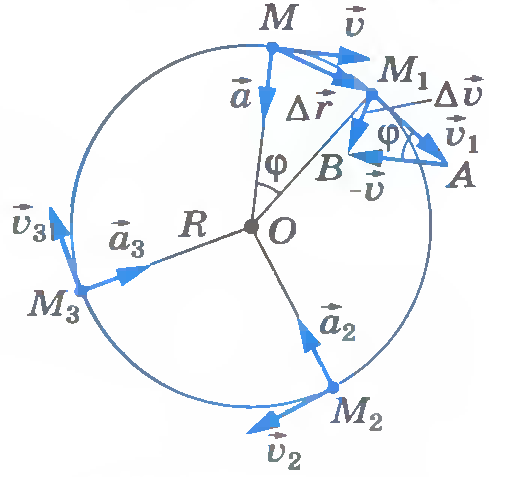
Рис.1
В связи с этим хочется предложить иной способ вывода формулы, основанный на представлениях Гюйгенса и всем известной теореме Пифагора. При этом следует сделать следующее замечание. Если тело движется по окружности, то, вообще говоря, различные его точки в одно и то же время проходят различные расстояния. Однако если радиус окружности значительно превосходит размеры тела, то можно описывать его движение как движение одной материальной точки. Движение материальной точки по окружности вполне характеризуется скоростью в каждой точке траектории. При равномерном вращении скорость изменяется только по направлению, а модуль скорости остается постоянным. Однако вычислить мгновенную скорость в каждой точке криволинейной траектории трудно и не всегда удобно. Поэтому для практических целей движение точки по окружности принято характеризовать линейной скоростью, которая является скалярной величиной и определяется длиной пути, пройденной точкой окружности за единицу времени. За промежуток времени 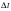 происходит некоторое изменение скорости
происходит некоторое изменение скорости 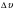 . Таким образом, при равномерном движении тела или точки по окружности возникает переменное по направлению ускорение.
. Таким образом, при равномерном движении тела или точки по окружности возникает переменное по направлению ускорение.
Выясним направление ускорения тела при его движении по окружности. Пусть за очень малый промежуток времени тело переместилось из точки А в точку В (рис.2). Тогда изменение вектора скорости 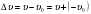 . Следовательно, для определения
. Следовательно, для определения 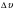 достаточно к вектору
достаточно к вектору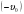 прибавить вектор
прибавить вектор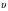 . Из рисунка видно, что вектор
. Из рисунка видно, что вектор 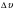 , равный разности
, равный разности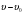 , направлен в сторону кривизны окружности в точке А. В этом случае вектор
, направлен в сторону кривизны окружности в точке А. В этом случае вектор 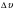 должен быть перпендикулярен вектору
должен быть перпендикулярен вектору 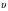 (так как между векторами
(так как между векторами 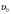 и
и 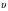 угол φ мал). Вектор скорости
угол φ мал). Вектор скорости 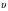 (как и
(как и 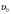 ) направлен по касательной, а касательная перпендикулярна радиусу. Отсюда следует, что вектор
) направлен по касательной, а касательная перпендикулярна радиусу. Отсюда следует, что вектор 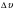 должен быть направлен по радиусу окружности, и направлен к ее центру. Из формулы
должен быть направлен по радиусу окружности, и направлен к ее центру. Из формулы 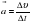 следует, что вектор ускорения имеет такое же направление, что и вектор
следует, что вектор ускорения имеет такое же направление, что и вектор 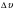 . Таким образом, учащиеся подводятся к выводу: вектор ускорения, возникающего при равномерном движении по окружности тела или точки, всегда направлен по радиусу к центру окружности. Поэтому такое ускорение называется центростремительным.
. Таким образом, учащиеся подводятся к выводу: вектор ускорения, возникающего при равномерном движении по окружности тела или точки, всегда направлен по радиусу к центру окружности. Поэтому такое ускорение называется центростремительным.
Рис.2
Теперь найдем модуль центростремительного ускорения. Пусть тело движется равномерно по окружности с радиусом R (рис.3). В данный момент времени тело находится в точке А и имеет скорость  .
.
Рис.3
Тело хочет двигаться равномерно и прямолинейно по инерции, но центростремительная сила возвращает его на линию окружности, при этом эта сила действует одновременно и непрерывно с движением тела по инерции, результатом чего является движение по окружности. Пусть отрезок АВ будет движением по инерции, а отрезок ВС будет возвратом тела на линию окружности. Тогда из треугольника ОАВ по теореме Пифагора




Подставляя эти обозначения в теорему Пифагора

Так как время t очень маленькое, то последним членом можно пренебречь. Тогда после преобразования этого выражения получится
 ,
,
где -линейная скорость тела,R-радиус окружности,
-линейная скорость тела,R-радиус окружности, - центростремительное ускорение.
- центростремительное ускорение.
Необходимо отметить, что при таком способе вывода формулы центростремительного ускорения целесообразней рассматривать равномерное движение точки по окружности не в кинематике, а в динамике, т.к. при получении формулы использовались понятия «инерция» и «центростремительная сила». По второму закону Ньютона ( ) ускорение всегда сонаправлено с силой, в результате действия которой оно возникает. Это справедливо и для центростремительного ускорения. Значит, и сила, под действием которой тело движется по окружности с постоянной по модулю скоростью, в каждой точке направлена по радиусу окружности к ее центру. В соответствии со вторым законом Ньютона и с формулой центростремительного ускорения модуль вектора этой силы определяется по формуле
) ускорение всегда сонаправлено с силой, в результате действия которой оно возникает. Это справедливо и для центростремительного ускорения. Значит, и сила, под действием которой тело движется по окружности с постоянной по модулю скоростью, в каждой точке направлена по радиусу окружности к ее центру. В соответствии со вторым законом Ньютона и с формулой центростремительного ускорения модуль вектора этой силы определяется по формуле

 .
.
Тела могут двигаться по окружности под действием сил разных видов. Например, шар легкоатлетического молота движется по окружности под действием силы упругости троса; планеты обращаются вокруг Солнца, а спутники - вокруг планет под действием силы всемирного тяготения; автомобиль совершает поворот за счет силы трения колес о дорогу; движение электронов вокруг ядра в атоме обусловлено действием сил электрического притяжения. Под действием этих сил возникает ускорение, меняющее направление скорости тела, благодаря чему оно движется по окружности или ее дуге.
Все физические теории отражают происходящие в природе процессы приближенно. Чтобы сформировать у учащихся представление об этом, можно провести оценку погрешности предложенной модели равномерного движения тела по окружности. Возьмём любое число меньше единицы, например, 0,1. В квадрате это число станет 0,01. Теперь у нас два числа, по формуле с сокращением последнего члена, и без его сокращения. Одно без сокращения 0,1 + 0,01 = 0,11, другое с сокращением 0,1. Эти два числа отличаются друг от друга на 10%. Если взять число 0,2, то погрешность составит 12%. Если взять число 0,9, то погрешность составит 19%. Таким образом, ошибка вычислений по формуле составляет от 10% до 19%, в зависимости от величины первой цифры, а эта цифра может быть любой.
Однако чтобы свести эту погрешность к минимуму, инженеры и астрономы вычисляют центростремительное ускорение с точностью до 5-7 знака. Если, например, взять число 0,00001 и произвести аналогичные операции, то мы получим отличие в 0,001%. При решении же школьных задач достаточно полученное значение ускорения округлить с точностью до сотых.
Предложенный способ вывода формулы центростремительного ускорения является наиболее простым и понятным для школьников и вносит ясность при рассмотрении равномерного движения точки по окружности как частного случая криволинейного движения.
Литература
Гюйгенс Х. Три мемуара по механике. Перевод, редакция и примечания профессора К.К. Баумгарта. Издательство Академии наук СССР, 1951.-376с.
Николаев С.А. О центростремительном ускорении.- URL: http://samlib.ru/n/nikolaew_s_a/ocentrostremitelxnomuskorenii.shtml. Дата обращения: 21.01.2013

 Получите свидетельство
Получите свидетельство Вход
Вход



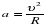 имеет свою историю возникновения. Первым, кто получил зависимость центростремительного ускорения от квадрата скорости и радиуса окружности, считается голландский физик и математик Христиан Гюйгенс (1629-1695гг.). В мемуарах «О центробежной силе» (этот трактат был опубликован только после смерти Гюйгенса в 1703г.) приведены 17 предположений с доказательствами. Предположения 2 и 3 доказывают для случая равных масс 1 и 2 следующие пропорции: если
имеет свою историю возникновения. Первым, кто получил зависимость центростремительного ускорения от квадрата скорости и радиуса окружности, считается голландский физик и математик Христиан Гюйгенс (1629-1695гг.). В мемуарах «О центробежной силе» (этот трактат был опубликован только после смерти Гюйгенса в 1703г.) приведены 17 предположений с доказательствами. Предположения 2 и 3 доказывают для случая равных масс 1 и 2 следующие пропорции: если 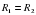 , то
, то 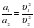 и если
и если 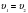 , то
, то 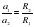 . Из этих теорем можно вывести общий случай, т.е. прямую пропорциональность центростремительного ускорения квадрату скорости и обратную пропорциональность радиусу
. Из этих теорем можно вывести общий случай, т.е. прямую пропорциональность центростремительного ускорения квадрату скорости и обратную пропорциональность радиусу 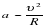 .
.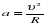 рассматриваются треугольники ОММ1 и М1АВ, которые подобны как равнобедренные с равными углами при вершинах (рис.1). Причем угол МОМ1 равен углу ВАМ1, т.к. соответствующие стороны перпендикулярны. Но учащиеся малознакомы с этой теоремой. В школьном курсе геометрии не акцентируется внимание на теорему, показывающую равенство углов, если соответствующие стороны перпендикулярны.
рассматриваются треугольники ОММ1 и М1АВ, которые подобны как равнобедренные с равными углами при вершинах (рис.1). Причем угол МОМ1 равен углу ВАМ1, т.к. соответствующие стороны перпендикулярны. Но учащиеся малознакомы с этой теоремой. В школьном курсе геометрии не акцентируется внимание на теорему, показывающую равенство углов, если соответствующие стороны перпендикулярны.
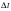 происходит некоторое изменение скорости
происходит некоторое изменение скорости 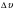 . Таким образом, при равномерном движении тела или точки по окружности возникает переменное по направлению ускорение.
. Таким образом, при равномерном движении тела или точки по окружности возникает переменное по направлению ускорение.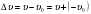 . Следовательно, для определения
. Следовательно, для определения 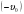 прибавить вектор
прибавить вектор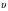 . Из рисунка видно, что вектор
. Из рисунка видно, что вектор 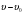 , направлен в сторону кривизны окружности в точке А. В этом случае вектор
, направлен в сторону кривизны окружности в точке А. В этом случае вектор 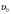 и
и 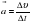 следует, что вектор ускорения имеет такое же направление, что и вектор
следует, что вектор ускорения имеет такое же направление, что и вектор 








 Методика изучения темы «Равномерное движение точки по окружности» в школьном курсе физики (0.12 MB)
Методика изучения темы «Равномерное движение точки по окружности» в школьном курсе физики (0.12 MB)
 0
0 851
851 67
67 Нравится
0
Нравится
0


