Методические рекомендации по выполнению внеаудиторной самостоятельной работы студентов по темам: "Растяжение и сжатие", "Кручение"

Введение

Самостоятельная работа студентов – это процесс активного, целенаправленного приобретения студентами новых знаний, умений без непосредственного участия преподавателя, характеризующийся предметной направленностью, эффективным контролем и оценкой результатов деятельности обучающегося.

Цели самостоятельной работы:

 - систематизация и закрепление полученных теоретических знаний и практических умений студентов;

 - углубление и расширение теоретических знаний;

 - формирование умений использовать нормативную, правовую, справочную документацию и специальную литературу;

 - формирование самостоятельности мышления, способностей к саморазвитию, самосовершенствованию и самореализации;

 - развитие исследовательских умений.

В данном пособии представлены методические рекомендации по выполнению внеаудиторной самостоятельной работы студентов по дисциплине « Техническая механика» по темам "Растяжение и сжатие", "Кручение".

Рекомендации состоят из четырёх частей.

Первая включает информационный материал, составленный на основании рабочей программы дисциплины.

Вторая часть рекомендаций содержит вопросы к информационному материалу и служит для осуществления самоконтроля.

Третья часть представляет собой инструкцию по решению конкретных задач.

В четвёртой части предложены задания для самостоятельного решения и ответы к задачам.

Работа с данными рекомендациями не предполагает усвоение новых знаний, но позволяет студенту углублять ранее полученные на лекциях и практических занятиях знания.

 «Растяжение и сжатие»

1. 1. Методические указания к решению задач по теме: «Растяжение - сжатие»

В результате изучения темы студенты должны:

Знать:

 - методику расчёта задач на прочность

Уметь:

 - строить эпюры нормальных сил и напряжений;

 - выполнять расчёт на прочность и подобрать поперечное сечение стержня.

Растяжением или сжатием называется такой вид деформации, при котором в поперечном сечении стержня возникает один внутренний силовой фактор – продольная сила N.

Величина последней равна алгебраической сумме проекций на продольную ось внешних сил, действующих на отсеченную часть стержня

N=∑ F_KZ (1)

Так как величина продольных сил в разных сечениях стержня неодинакова, то строится эпюра продольных сил, т. е. график, показывающий изменения величины продольных сил в сечении стержня по его длине.

Под действием продольных сил в поперечном сечении стержня возникает нормальное напряжение, которое определяется по формуле:

σ =N/А

где А - площадь поперечного сечения стержня.

При решении первой задачи от студента требуется умение строить эпюры продольных сил, нормальных напряжений и определять удлинение или укорочение стержня.

Последовательность построения эпюр продольных сил:

Разбиваем стержень на участки, ограниченные точками приложения сил (нумерацию участков ведём от незакрепленного конца).

Используя метод сечений, определяем величину продольных сил в сечении каждого участка.

Выбираем масштаб и строим эпюру продольных сил, т. е. под изображением стержня проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответственно в выбранном масштабе продольным силам (положительное значение откладываем вверх (или в право) отрицательное - вниз ( или влево).

Последовательность построения эпюр нормальных напряжений.

Разбиваем стержень на участки, ограниченные точками приложения сил и там, где меняется площадь сечения.

Строим эпюру нормальных сил, по формуле 1 определяем нормальные напряжения на каждом участке.

Весь материал – смотрите документ.

ДЕПАРТАМЕНТ ОБРАЗОВАНИЯ И МОЛОДЁЖНОЙ ПОЛИТИКИ

ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА-ЮГРЫ

БЮДЖЕТНОЕ УЧРЕЖДЕНИЕ

СРЕДНЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

ХАНТЫ-МАНСИЙСКОГО АВТОНОМНОГО ОКРУГА-ЮГРЫ

«НЯГАНСКИЙ ПРОФЕССИОНАЛЬНЫЙ КОЛЛЕДЖ»

МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

по выполнению внеаудиторной самостоятельной работы студентов

по дисциплине: «Техническая механика»

по темам: "Растяжение и сжатие", "Кручение"

Составил преподаватель: С.А. Шарипова

Нягань, 2014

Содержание

Введение 3

1. «Растяжение и сжатие» 4

1.1 Методические указания к решению задач по теме «Растяжение

и сжатие» 4

1.2 Вопросы для самопроверки 6

1.3 Порядок решения типовых задач 6

1.4 Задания для самостоятельного решения 8

2. «Кручение» 10

2.1 Методические указания к решению задач по теме «Кручение» 10

2.2 Вопросы для самопроверки 13

2.3 Порядок решения типовых задач 14

2.4 Задания для самостоятельного решения 17

Список литературы 19

"Скажи мне и я забуду. Покажи мне и я запомню.

Дай мне действовать самому и я научусь."

Китайская мудрость

Введение

Самостоятельная работа студентов – это процесс активного, целенаправленного приобретения студентами новых знаний, умений без непосредственного участия преподавателя, характеризующийся предметной направленностью, эффективным контролем и оценкой результатов деятельности обучающегося.

Цели самостоятельной работы:

- систематизация и закрепление полученных теоретических знаний и практических умений студентов;

- углубление и расширение теоретических знаний;

- формирование умений использовать нормативную, правовую, справочную документацию и специальную литературу;

- формирование самостоятельности мышления, способностей к саморазвитию, самосовершенствованию и самореализации;

- развитие исследовательских умений.

В данном пособии представлены методические рекомендации по выполнению внеаудиторной самостоятельной работы студентов по дисциплине « Техническая механика» по темам "Растяжение и сжатие", "Кручение".

Рекомендации состоят из четырёх частей.

Первая включает информационный материал, составленный на основании рабочей программы дисциплины.

Вторая часть рекомендаций содержит вопросы к информационному материалу и служит для осуществления самоконтроля.

Третья часть представляет собой инструкцию по решению конкретных задач.

В четвёртой части предложены задания для самостоятельного решения и ответы к задачам.

Работа с данными рекомендациями не предполагает усвоение новых знаний, но позволяет студенту углублять ранее полученные на лекциях и практических занятиях знания.

1. «Растяжение и сжатие»

1.1. Методические указания к решению задач по теме: «Растяжение-сжатие»

В результате изучения темы студенты должны:

Знать:

- методику расчёта задач на прочность

Уметь:

- строить эпюры нормальных сил и напряжений;

- выполнять расчёт на прочность и подобрать поперечное сечение стержня.

Растяжением или сжатием называется такой вид деформации, при котором в поперечном сечении стержня возникает один внутренний силовой фактор – продольная сила N.

Величина последней равна алгебраической сумме проекций на продольную ось внешних сил, действующих на отсеченную часть стержня

N=∑ F_KZ (1)

Так как величина продольных сил в разных сечениях стержня неодинакова, то строится эпюра продольных сил, т.е. график, показывающий изменения величины продольных сил в сечении стержня по его длине.

Под действием продольных сил в поперечном сечении стержня возникает нормальное напряжение, которое определяется по формуле:

σ =N/А

где А- площадь поперечного сечения стержня.

При решении первой задачи от студента требуется умение строить эпюры продольных сил, нормальных напряжений и определять удлинение или укорочение стержня.

Последовательность построения эпюр продольных сил:

Разбиваем стержень на участки, ограниченные точками приложения сил (нумерацию участков ведём от незакрепленного конца).

Используя метод сечений, определяем величину продольных сил в сечении каждого участка.

Выбираем масштаб и строим эпюру продольных сил, т.е. под изображением стержня проводим прямую, параллельную его оси, и от этой прямой проводим перпендикулярные отрезки, соответственно в выбранном масштабе продольным силам (положительное значение откладываем вверх (или в право) отрицательное - вниз ( или влево).

Последовательность построения эпюр нормальных напряжений.

Разбиваем стержень на участки, ограниченные точками приложения сил и там, где меняется площадь сечения.

Строим эпюру нормальных сил, по формуле 1 определяем нормальные напряжения на каждом участке.

По полученным значениям в масштабе строим эпюру нормальных напряжений.

Удлинение ( укорочение ) стержня определяется по формуле Гука.

где Е – модуль Юнга ( для стали Е=2·10 ⁵ МПа ).

Удлинение (укорочение) определяется на каждом участке стержня, а затем находят алгебраическую сумму полученных значений. Это будет ∆l стержня. Если ∆l положительна, то брус удлиняется, если ∆l отрицательна, то укорачивается.

При решении ряда задач необходимо ясно представлять смысл условия прочности при растяжении – сжатии, знать, что исходя из условия прочности, можно производить три вида расчётов:

а) проверочный, при котором проверяется выполнено ли условие прочности σ≤ [σ] ( или n≥ [n]);

б) определение допускаемой нагрузки;

в) проектный, при котором определяются необходимые размеры поперечных сечений бруса, обеспечивающие заданную прочность.

Студенты должны также уметь пользоваться в ходе решения всеми необходимыми формулами и правильно выполнять вычисления.

1.2. Вопросы для самопроверки

1. Внутренние силовые факторы при растяжении-сжатии. Метод сечений.

2. Нормальные напряжения при растяжении.

3. Как нужно нагрузить прямой брус, чтобы он работал на растяжение?

4. Как определяется напряжение в любой точке поперечного сечения при растяжении (сжатии)?

5. Каков физический смысл модуля продольной упругости Е?

6. Что такое допускаемое напряжение и как оно выбирается в зависимости от механических свойств материала?

7. Сколько различных видов расчёта, и какие расчеты можно проводить, используя условие прочности?

1.3. Порядок решения типовых задач

Двухступенчатый стальной брус нагружен силами F₁=30 кН F₂=40 кН.

Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение ∆l свободного конца бруса, приняв Е=2∙10 ⁵ МПа. Площади поперечных сечений А₁=1,5см²?; А ₂ =2см²?

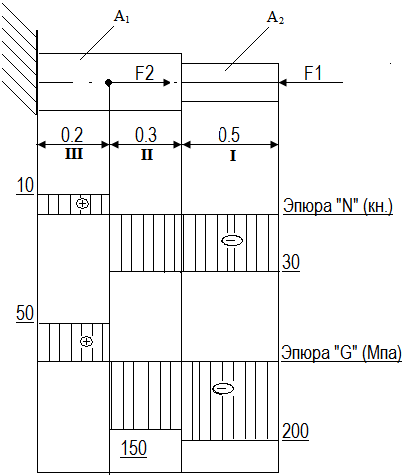
Задача требует от студента умения строить эпюры продольных сил, нормальных напряжений и определять удлинения и укорочения бруса.

Последовательность решения задачи

1. Разбить брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, а для напряжений также и место изменения размеров поперечного сечения.

2. Определить по методу сечений продольную силу для каждого участка (ординаты эпюры N) и построить эпюры продольных сил N. Проведя – параллельно оси бруса базовую (нулевую) линию эпюры, отложить перпендикулярно ей в произвольном масштабе получаемые значения ординат. Через концы ординат провести линии, проставить знаки и заштриховать эпюру линиями, параллельными ординатам.

3. Для построения эпюры нормальных напряжений определяем напряжения в поперечных сечениях каждого из участков. В пределах каждого участка напряжения постоянные, т.е. эпюра на данном участке изображается прямой, параллельной оси бруса.

Перемещение свободного конца бруса определяем как сумму удлинений (укорочений) участков бруса, вычисленных по формуле Гука.

Решение:

Разбиваем брус на участки.

Определяем ординаты эпюры N на участках бруса:

N₁= - F₁= -30кН

N₂= - F₂= -30кН

N₃= -F₁+F₂= -30+40=10 кН

Строим эпюру продольных сил

Вычисляем ординаты эпюры нормальных напряжений

σ₁ = N_1/А₂ = –200МПа

σ₂ = N_1/А₁ = –150МПа

σ ₃= N_2/А₁ = 50МПа

Строим эпюры нормальных напряжений.

4. Определяем перемещение свободного конца бруса

∆l=∆l₁+∆l₂+∆l₃

∆l₁= – 0,5мм

∆l₂= – 0,225мм

∆l₃= 0,05мм

∆l= - 0,5 – 0,225 + 0,05 = – 0,675мм

Ответ: итог отрицательный значит брус укоротился на 0,675мм

1.4. Задания для самостоятельного решения

Задача №1

Проверить прочность стальной тяги ВО диаметром d=20мм,если предел текучести σ_т =240МПа.требуемый коэффициент запаса прочности [n]=1,5

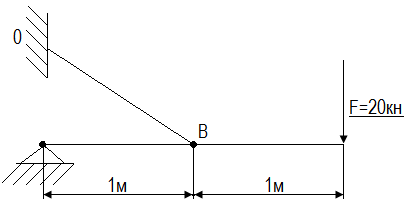
Ответ: перегружена на 58,75%

Задача 2.

Проверить прочность стальных брусьев, если [σ]=160МПа

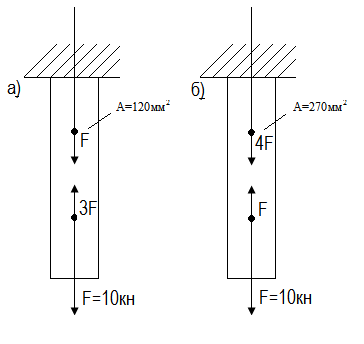
Ответ: а) перегружен на 4,4%; б) недогружен на 7,5%

Задача 3.

Определить требуемую площадь А поперечного сечения стального бруса, если [σ]=160МПа,

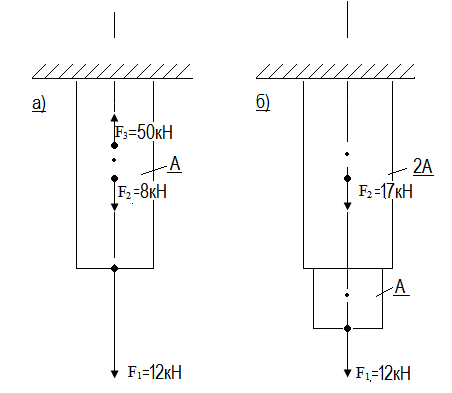Ответ: а) А=188мм² ; б) А=90,6мм²

Задача 4. Проверить прочность ступенчатого стержня.

Р = 20 кН, А = 10 см², []=10 кН см², а = 1м

1.1 1.2 1.3 1.4

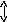
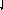
А

3А

А

P

P

P

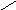
P

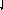
а

а

2А

P

P

P

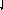
а

А

2А

P

P

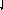
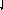
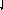
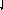
2а

2А

2А

А

2. «Кручение»

2.1 Методические указания к решению задач на прочность и жесткость по теме: «Кручение»

В результате изучения темы студенты должны:

Знать:

- методику расчета на прочность и жесткость.

Уметь:

- строить эпюру крутящих моментов;

- выполнять расчеты на прочность и жесткость и подобрать сечение вала.

Кручением называют такой вид нагружения бруса, при котором в его сечениях возникает только один внутренний силовой фактор – крутящий момент Mz. Крутящий момент в произвольном поперечном сечении бруса равен алгебраической сумме внешних (скручивающих) моментов, действующих на отсеченную часть.

Будем считать крутящий момент положительным, если для наблюдателя смотрящего на проведенное сечение он представляется направленным по часовой стрелке.

Условие прочности при кручении имеет вид:

τ_=_τk],

где Mz max – наибольший крутящий момент

Wp – полярный момент сопротивления сечения

[τk] – допускаемое касательное напряжение на кручение.

При проверочном расчете определяют τmax и сравнивают с допускаемым значением [τk], затем делают вывод о прочности.

Для подбора поперечного сечения балки (проектного расчета) из условия прочности определяют необходимое значение полярного момента сопротивления сечения. Wp ≥ _

Для сечения вала с кольцеобразным поперечным сечением

Wp ≈ 0,2×_ → d ≈ _

Для сечения вала с кольцеобразным поперечным сечением

Wp ≈ 0,2×_×(1-_), → D ≈ _

Где С = _

d – внутренний диаметр кольца

D – наружный диаметр кольца

Полученные значения диаметра, выраженное в миллиметрах, следует округлить в сторону увеличения до ближайшего целого четного числа или числа, оканчивающего на 5

Условие жесткости при кручении имеет вид:

_ = _ ≤ [_],

Где _ – относительный угол закручивания.

Jp – полярный момент инерции сечения

G – модуль сдвига (для стали G = 8×_МПа)

[_] – допускаемый относительный угол закручивания.

При проверочном расчете определяют _ и сравнивают с [_], затем делают вывод соблюдено или нет условие жесткости.

При проектном расчете из условия жесткости определяют требуемый полярный момент инерции сечения.

Jp ≥ _

Исходя из формы поперечного сечения вала (круг или кольцо) по найденному значению Jp определить диаметр (вычисленное значение диаметра следует округлить до ближайшего целого четного числа или числа оканчивающегося на 5)

Для круга: Jp ≈ 0,1×d → d ≈ _

Для кольца: Jp ≈ 0,1×_×(1-_) → D ≈ _

Если проектный расчет вала проводиться из условия прочности и из условия жесткости, то из двух вычисленных значений диаметра вала следует выбрать больший.

В Международной системе единиц (СИ) передаваемая валом мощность измеряется в ваттах (Вт), угловая скорость ω в _,вращающие моменты Мвр, а также крутящие моменты Mz в Н×М, допускаемые касательные напряжения [_ в Па, полярные моменты инерции сечений Jp в _, полярные моменты сопротивления Wp – в _, допускаемый угол закручивания [_] в _, модуль сдвига G – в Па.

В соответствии с этим необходимо заданную частоту вращения (если она дается в условии задачи) выразить в единицах угловой скорости (_), применив известную формулу: ω = _,

тогда зависимость между передаваемой мощностью P в кВт, угловой скоростью ω, _и выраженным внешним моментом Мвр в Н×М, скручивающим вал, запишется в таком виде: Мвр = _.

2.2. Вопросы для самопроверки

1. Какой внутренний силовой фактор возникает в поперечном сечении вала, и какое напряжение он вызывает?

2. Сформулируйте правило определения крутящего момента в произвольном сечении вала и правило знаков.

3. Запишите условие прочности и жесткости при кручении.

4. Как определить полярные моменты инерции и сопротивления для круга и кольца?

5. Как нужно нагрузить брус, чтобы он работал только на кручение?

6. По какому закону распределяется напряжение в поперечном сечении круглого бруса при кручении?

7. Сколько различных видов расчета можно производить из условия прочности и жесткости?

2.3. Порядок решения типовых задач

Задача 1.

Определить диаметр стального вала для передачи мощности Р=8кВт при частоте вращения 240 _ из условия прочности, принять [_]=60МПа. Определив требуемый диаметр вала, найти угол его закручивания на длине l=300мм.

Дано:

Р=8кВт

n=240_

[_]=60МПа

l=300мм

G=8_МПа

d-? φ-?

Решение:

1.Определяем крутящий момент

Мвр = Мz = _ = _;

ω = _;

Мz = _ = 0,318кН_М = 318Н_М

2. Определяем диаметр вала, используя условие прочности на кручение.

_ = _ ≤ [_]→_ ≥ _ = _ = 5,3*_

_ = _ → d = _ = _ = 30мм.

3. Определяем угол закручивания

φ = _ = _

Jp = _

φ = _ = 0,015 рад

Задача 2

Определить диаметр стального вала из условия жесткости, передающего мощность _=60кВт; _=120кВт и _=80кВт при угловой скорости ω=60_, если допускаемое касательное напряжение [_]=30МПа, а допускаемый относительный угол закручивания [_]=0,02 _.

Определяем скручивающие моменты

_ = _ = _ = 1000Н*М

_ = _ = _ = 2000Н*М

_ = _ = _ = 1333Н*М

Σ _= 0

_-_-_+_= 0→_= _-_

_= 2000+1333-1000 = 2333Н*М

2. Вычисляем крутящие моменты на каждом участке вала и строим эпюру крутящих моментов участок

-_+_= 0

_= _= 1000 Н*М

участок 1

-_+_+_=0

_= _-_=1000-2000 = -1000 Н*М

участок 2

-_+_+_+_= 0

_= _-_-_=1000 – 2000 – 1333 = -2333 Н*М

3. Определяем из условия прочности диаметр вала.

_= _ ≤ [_] → _ ≥ _;

_ ≥ _ =77767_;

_= _ → d =_ ≈73мм.

4. Определяем из условия жесткости диаметр вала

_= _ ≤ [_] → Jp ≥ _ = _ =1458125 _

Jp = _ → d =_ =_ = 62мм

5. Окончательно принимаем диаметр вала d=75 мм.

2.4. Задания для самостоятельного решения

Задача 1

Для заданных брусьев, построить эпюру крутящих моментов и определить опасное сечение.

Ответ: Mz max a) 2m; б) 4m; в) 4m; д) 18кНМ; е) 45кНМ

Задача 2

Определить отношение диаметров и масс двух валов одинаковой прочности и длины, передающих одинаковую мощность, если один вал вращается n₁=800мин^-1, другой с n₂=1200мин^-1.

Ответ: d₁:d₂=1,15; m₁:m₂=1,31

Задача 3

Стальной вал вращается с частотой вращения n=980мин^-1 и передает мощность Р=40кВт. Определить требуемый диаметр вала , если допускаемое касательное напряжение [τ_к]=25МПа

Ответ: d=43мм.

Задача 4

Проверить прочность и жесткость стальных брусьев, если [τ_к]=40МПа; [φ₀]=0,6 _

Ответ: а) τ_max=68,4МПа; φ_{0 max}=1,63 _;

б) τ_max=27,6 МПа; φ_{0 max}=0,4 _.

Задача 5

Определить требуемые размеры поперечного сечения бруса, если предел текучести τ_m=140 МПа, а требуемый коэффициент запаса прочности [n]=2,5

Ответ: d=65мм

Список литературы

1. Ицкович Г.М. «Сопротивление материалов» М.: Высшая школа, 200 Аркуша А.И. «Техническая механика», «Теоретическая механика и сопротивление материалов». М.: Высшая школа, 2002

2. Вереина Л.М, Краснов М.М. «Техническая механика» М.: Академия, 2008

3. Иукович Г.М. «Сопротивление материалов» М. «Высшая школа» 2004г

4. Иукович Г.М. «Сборник задач по сопротивлению материалов» М.«Высшая школа» 2001г.

5. Мовнин М.С. и другие «Руководство к решению задач по технической механике» М. «Высшая школа» 2006г.

24