"Возьми столько, сколько ты можешь и хочешь, но не меньше обязательного".
Цели урока:
знать и уметь записывать определение логарифма, основного логарифмического тождества;
уметь применять определение логарифма и основное логарифмическое тождество при решении упражнений;
познакомиться со свойствами логарифмов;
научиться различать свойства логарифмов по их записи;
научиться применять свойства логарифмов при решении заданий;
закрепить вычислительные навыки;
продолжить работу над математической речью.
формировать навыки самостоятельной работы, работы с учебником, навыки самостоятельного добывания знаний;
развивать умение выделять главное при работе с текстом;
формировать самостоятельность мышления, мыслительных операций: сравнение, анализ, синтез, обобщение, аналогия;
показать учащимся роль систематической работы по углублению и повышению прочности знаний, по культуре выполнения заданий;
развивать творческие способности студентов.
Базовые знания:
определение показательного уравнения, основные методы и приёмы решения показательных уравнений;
Тип урока: сообщение новых знаний.
Методы работы:
проблемный;
частично-поисковый.
Виды работ:
индивидуальная;
коллективная;
индивидуально-коллективная;
фронтальная.
Мотивация познавательной деятельности: на занятии необходимо предоставить студентам возможность проявить сообразительность, смекалку в формировании навыков самостоятельной работы, работы с учебником, навыков самостоятельного добывания знаний.
Оборудование:
таблица свойств логарифмов;
текст «Из истории логарифмов»;
плакаты;
карточки-задания;
обучающие карточки;
набор тестов;
ПК учителя, мультимедийный проектор;

Презентация, содержащая материал для повторения и закрепления теоретических знаний, для отработки навыков практического применения теории к решению упражнений, создания проблемной ситуации, для самоконтроля, содержащая сведения из истории логарифмов
План урока.
Организационный момент.
Постановка цели.
Проверка ранее изученного материала
Введение понятия логарифм.
Определение логарифма.
Историческая справка
Основное логарифмическое тождество.
Основные свойства логарифмов
Подведение итогов.
Домашнее задание.
Ход урока.
1. Организационный момент.
Приветствие.
2. Постановка цели.
- Ребята, сегодня на уроке вам предстоит проверить умения решать простейшие показательные уравнения, чтобы можно было ввести новое для вас понятие, затем познакомимся со свойствами нового понятия; вы должны научиться различать эти свойства по их записи; научиться применять эти свойства при решении заданий.
Будьте собраны, внимательны и наблюдательны. Успехов!
3. Проверка ранее изученного материала (слайды 2–3)
Студентам предлагается определить тему урока, решив уравнения.
– Назовите новое понятие, с которым мы познакомимся...
4. Введение понятия логарифм. (слайд 4)
– Тема нашего урока “Логарифм, его свойства”. Попробуйте найти корень уравнения
2х = 5. Ответ данного уравнения мы можем записать с помощью нового понятия. Прочитайте текст слайда и запишите корень уравнения.
4.1. Определение логарифма (слайд 7)
Логарифмом положительного числа b по основанию a, где a>0, a ≠ 1 называется показатель степени, в которую надо возвести a, чтобы получить число b.
Весь материал - в документе.
4.2. Историческая справка (слайды 9–11)
Из истории логарифмов.
Слово логарифм происходит из двух греческих слов и оно переводится, как отношение чисел.
В течение ХVI в. резко возрос объем работы, связанный с проведением приближенных вычислений в ходе решения разных задач, и в первую очередь задач астрономии, имеющей непосредственное практическое применение (при определения положения судов по звездам и по Солнцу).
Логарифмы необычайно быстро вошли в практику. Изобретатели логарифмов не ограничились разработкой новой теории. Было создано практическое средство – таблицы логарифмов, - резко повысившее производительность труда вычислителей.
Логарифмы необычайно быстро вошли в практику. Изобретатели логарифмов не ограничились разработкой новой теории. Было создано практическое средство – таблицы логарифмов, - резко повысившее производительность труда вычислителей.
4.3. Основное логарифмическое тождество (слайд 12)
В записи b=at число a является основанием степени, t - показателем, b - степенью. Число t - это показатель степени, в которую надо возвести основание a, чтобы получить число b. Следовательно, t - это логарифм числа b по основанию a: t=logab.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



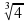 ; 3х =
; 3х =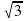 ; 5х =
; 5х = 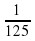 ; 2х =
; 2х = 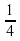 ;
; 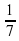 ; 3х =
; 3х = 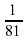
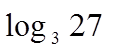
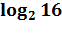
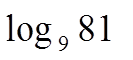
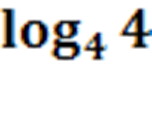
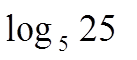
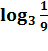
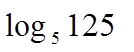

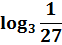
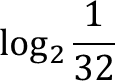
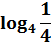
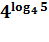
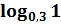
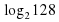









 Методическая разработка урока по математике "Логарифм и его свойства" (72.1 КB)
Методическая разработка урока по математике "Логарифм и его свойства" (72.1 КB)
 1
1 1262
1262 329
329 Нравится
0
Нравится
0


