Метод введения нового переменного (метод замены переменной).
Этот метод, метод замены переменного, вообще говоря, применяется не только к решению систем уравнений, но и для решения уравнений вообще.
Суть метода заключается в том, чтобы одинаковые составляющие части уравнения, содержащие переменные заменить на новую переменную.
Пример 6:
Дано уравнение:
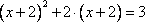
Требуется решить уравнение, введя новую переменную.
Решение:
В этом уравнении переменная х присутствует только в выражении вида 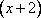 и нигде больше. Введем новую переменную (сделаем замену):
и нигде больше. Введем новую переменную (сделаем замену):
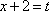
Уравнение примет вид:
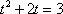
Замечание: требуется сделать замену так, чтобы старой переменной х не осталось. Только t.
Решим это обыкновенное квадратное уравнение:
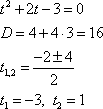
Теперь не следует забывать, что найти значения переменной х, а найдены пока значения переменной t.
Сделаем обратную замену (вернемся к переменной х):
1) пусть 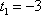
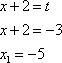
2) пусть 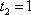
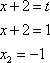
Всё, поставленная задача выполнена.
Ответ: 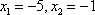 .
.
Попробуем теперь решить систему этим методом.
Пример 6:
Решить систему уравнений:
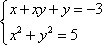
Решение:
Проведем преобразование уравнений, такое, чтобы сделать замену.
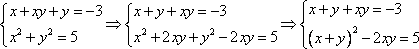
Замечание: Старых переменных 2 шт., значит и новых должно быть 2 шт.
В этой системе видно, что старые переменные сгруппированы таким образом, что располагаются только в выражениях вида 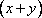 и
и 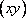 . Введем новые переменные (сделаем замену переменных).
. Введем новые переменные (сделаем замену переменных).
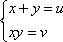
Система примет вид:
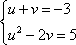
Она достаточно проста, решим полученную систему методом подстановки:
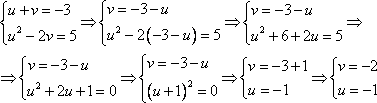
Так, значения новых переменных найдены, вернемся к старым:
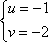
Тогда:
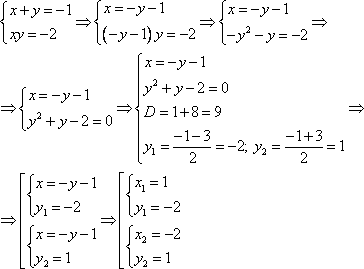
Ответ: 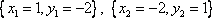


 Получите свидетельство
Получите свидетельство Вход
Вход



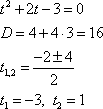
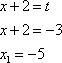
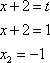
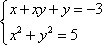
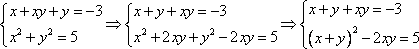
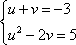
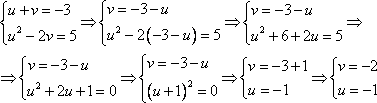
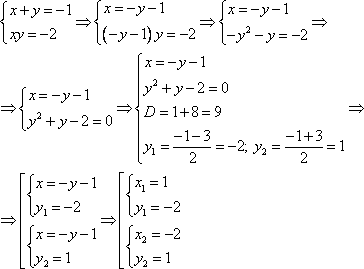









 Метод введения новой переменной (метод замены переменной) (методический материал) (27.11 КB)
Метод введения новой переменной (метод замены переменной) (методический материал) (27.11 КB)
 0
0 2817
2817 89
89 Нравится
0
Нравится
0


