Меодическая разработка по математике "Критические точки функции, ее максимумы и минимумы"

В системе упражнений, предлагаемой по данной теме, основное внимание уделяется закреплению умения определять точки максимума (минимума) и знания достаточных условий точек экстремума, что способствует предотвращению ошибок, которые наиболее часто допускают учащиеся при изучении этого материала. В связи с этим сюда включены вопросы на распознавание точек максимума (минимума), задания на изображение функции, имеющей указанные точки экстремумов, задачи на вывод следствий из определения. Знание достаточных условий существования точек экстремума закрепляется на упражнениях, в которых нужно непосредственно, без каких - либо дополнительных вычислений или преобразований, применить теорему. Усвоение учащимися достаточных условий преподаватель может проверить по результатам выполнения математического диктанта.

  Карточки - задания самостоятельной работы обучающего характера содержат план нахождения точек экстремумов для различных функций, который сводится к трем основным действиям: нахождению производной функции, отысканию критических точек и «испытанию» их на точки экстремума, т. е. проведению сравнения знаков производной в левой и правой полуокрестностях каждой из критических точек. Так как работа обучающая, то в один из вариантов ее включена «памятка» для определения точек максимума и минимума.

 Задания для устного опроса охватывают, наиболее существенные моменты изложения темы. Так, вопросы, подводящие к определению точек максимума и минимума, обращают внимание учащихся на то, что, во - первых, это внутренние точки области определения; во - вторых, только в некоторой окрестности должно выполняться одно из неравенств. С графической иллюстрацией связано рассмотрение и возможных соотношений между значениями в точках максимума и минимума. В систему вопросов и упражнений включены и такие задания, которые требуют от учащихся умения не только установить наличие экстремума, но и объяснить, почему в данной точке экстремума нет. Затем на примерах рассматривается необходимое условие существования в точке экстремума.

Система упражнений

2 (устно). Назовите точки максимума и минимума функций, графики которых изображены на рисунке. Ответ обоснуйте.

3. Схематично изобразите график какой - либо функции f, для которой х1 = - 3 – точка максимума, х2 = 4 – точка минимума.

4. Схематично изобразите график какой - либо функции g, которая имеет две точки максимума и одну точку минимума.

5 (устно). Назовите экстремумы для каждой из функций, графики которых изображены на рисунке.

Методическая разработка темы по математике

«Критические точки функции,

ее максимумы и минимумы»

Преподаватель: Талицких Т. С.

Критические точки функции, ее максимумы и минимумы

В системе упражнений, предлагаемой по данной теме, основное внимание уделяется закреплению умения определять точки максимума (минимума) и знания достаточных условий точек экстремума, что способствует предотвращению ошибок, которые наиболее часто допускают учащиеся при изучении этого материала. В связи с этим сюда включены вопросы на распознавание точек максимума (минимума), задания на изображение функции, имеющей указанные точки экстремумов, задачи на вывод следствий из определения. Знание достаточных условий существования точек экстремума закрепляется на упражнениях, в которых нужно непосредственно, без каких-либо дополнительных вычислений или преобразований, применить теорему. Усвоение учащимися достаточных условий преподаватель может проверить по результатам выполнения математического диктанта.

Карточки-задания самостоятельной работы обучающего характера содержат план нахождения точек экстремумов для различных функций, который сводится к трем основным действиям: нахождению производной функции, отысканию критических точек и «испытанию» их на точки экстремума, т.е. проведению сравнения знаков производной в левой и правой полуокрестностях каждой из критических точек. Так как работа обучающая, то в один из вариантов ее включена «памятка» для определения точек максимума и минимума.

Задания для устного опроса охватывают, наиболее существенные моменты изложения темы. Так, вопросы, подводящие к определению точек максимума и минимума, обращают внимание учащихся на то, что, во-первых, это внутренние точки области определения; во-вторых, только в некоторой окрестности должно выполняться одно из неравенств: _ С графической иллюстрацией связано рассмотрение и возможных соотношений между значениями в точках максимума и минимума (например, _). В систему вопросов и упражнений включены и такие задания, которые требуют от учащихся умения не только установить наличие экстремума, но и объяснить, почему в данной точке экстремума нет. Затем на примерах рассматривается необходимое условие существования в точке экстремума.

Система упражнений

1 (устно). На рисунке изображены графики функций. Укажите, для каких из них точки 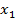_, _, _ являются точками максимума или минимума. Ответ поясните.

2 (устно). Назовите точки максимума и минимума функций, графики которых изображены на рисунке. Ответ обоснуйте.

3. Схематично изобразите график какой-либо функции _, для которой _ = -3 – точка максимума, _ = 4 – точка минимума.

4. Схематично изобразите график какой-либо функции _, которая имеет две точки максимума и одну точку минимума.

5 (устно). Назовите экстремумы для каждой из функций, графики которых изображены на рисунке.

6. Функция _ непрерывна в точке _ = 2, причем _ на промежутке ]0; 2[ и _ на промежутке ]2; 3[. Является ли точка _ = 2 точкой максимума или минимума?

7. Функция _ непрерывна в точке _ = -3, причем _ на промежутке ]-3,5; -3[ и 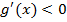_ на промежутке ]-3; 0[. Является точка _ = -3 точкой максимума или точкой минимума?

8. Функция _ непрерывна в точке _ = 8, причем _ на промежутке ]7; 8[ и _ на промежутке ]8; 9[. Будет точка _ = 8 точкой максимума или минимума?

9. Дифференцируемая функция _ на промежутке [4; 9] имеет единственную точку экстремума – точку максимума _ = 3. Определите знак производной на каждом из промежутков [4; 3[ и ]3; 9].

10. Функция _ на промежутке [-5; 7] имеет единственную точку экстремума – точку минимума _ = -2. Определите знак производной на каждом из промежутков [-5; -2[ и ]-2; 7], если функция _ дифференцируема.

Математический диктант

Вариант 1. Известно, что функция _ непрерывна на всем рассматриваемом промежутке. Установите, есть ли у функции точки экстремума, запишите точки максимума и минимума, если:

а) _ на промежутке [-4; 2[; б) _на промежутке ]2; 5[;

в) _ на промежутке]5; ∞[.

Вариант 2. Известно, что функция _ непрерывна на всем рассматриваемом промежутке. Установите, есть ли у функции точки экстремума, запишите точки максимума и минимума, если:

а) _ на промежутке ]-∞; -1[; б) _ на промежутке ]-1; 7[;

в) _ на промежутке ]7; ∞[.

Самостоятельная работа (СО)

Вариант 1. Определите точки экстремума функции _ x3 – x.

План решения:

1) Найдите производную функции _.

2) Определите критические точки функции (т.е. решите уравнение _ и найдите точки, если такие есть, в которых производная не существует).

3) Установите знак производной в каждом из промежутков, на которые критические точки делят область определения функции.

Помните: а) _ – точка максимума, если _ непрерывна в точке _; _ на интервале ]a, _[ и _ на интервале ]_, b[, где a b;

б) _ – точка минимума, если _ непрерывна в точке _, _ на интервале ]a; _[ и _ на интервале ]_, b[, где a b.

4) Запишите ответ.

Вариант 2. Найдите точки экстремума функции _.

План решения:

1) Найдите производную функции.

2) Определите критические точки функции (т.е. решите уравнение _ и найдите точки, если такие есть, в которых производная не существует).

3) Установите знак производной в окрестности критической точки.

4) Для каждой из критических точек проверьте выполнение достаточных условий точек максимума и минимума.

5) Запишите ответ.

Вариант 3. Найдите точки экстремума функции _

План решения:

1) Найдите производную функции.

2) Определите критические точки функции.

3) Установите знак производной в окрестностях критических точек.

4) Проверьте выполнение достаточных условий точек экстремума, используя результат п. 3 плана.

5) Запишите ответ.

Вариант 4. Найдите точки экстремума функции _.

План решения:

1) Найдите производную функцию.

2) Определите критические точки функции.

3) Определите знак производной в окрестностях критических точек.

4) Примените достаточные условия точек экстремума.

5) Запишите ответ.

Устный опрос

1. Сколько точек экстремума изображено на каждом из графиков функции?

2. Назовите точки экстремума функций и значения функций в них.

3. Каков характер монотонности функции на некотором промежутке слева (справа) от точки максимума (минимума)?

4. Сравните значения, которые принимает функция в некоторой окрестности точки максимума (минимума) со значением в самой точке. Запишите эти соотношения в виде неравенств.

5. Дайте определение точек максимума и минимума.

6. Каково необходимое условие существования экстремума в точке? Как расположена касательная к графику функции в точке с абсциссой _ , если _? Достаточно ли это условие для существования экстремума в точке _?

7. Пользуясь графиками функций на рисунке, назовите знаки производной в окрестностях точки экстремума. Поясните, при каком условии имеется в точке максимум (минимум).

8. Имеют ли функции, графики которых изображены на рисунке, экстремум в точке _? Существует ли у функций производная в этой точке? Сделайте вывод.

9. Являются ли точки – 7 и 5 критическими точками, если функция _ задана на отрезке [-7; 5]? Если нет, объясните, почему.

10 (письменно). Найдите критические точки функций:

а) _; б) _; в) _; x€] – 7; 1];

г) _; д) _, x€ [-3; -1) ].

11. Установите, имеют ли приведенные в задании 10 функции экстремумы в найденных критических точках. Если имеют, то объясните, какие.

12. Может ли значение в точке максимума (минимума) быть меньше (больше) значения в точке минимума (максимума)? Проиллюстрируйте ответ на графике функции.