Конспект урока
ФИО учителя: Расулова Зарима Джамалудиновна
Место работы: МБОУ СОШ №7 им. Мирзакеримова, г. Дагестанские Огни
Предмет: алгебра
Класс: 7
УМК: Алгебра. 7 класс. Учебник (авторы: Ю.Н.Макарычев, Н.Г.Миндюк, К.И.Нешков, С.Б.Суворов / под редакцией С.А.Теляковского.), издательство М.: Просвещение, 2018 г.
Тема урока «Умножение одночлена на многочлен".
Цели урока:
Методическая:
-
организовать работу класса по обобщению распределительного свойства.
Образовательная:
-
применение распределительного свойства к умножению одночлена на многочлен;
-
геометрический смысл умножения одночлена на многочлен;
-
применение алгоритма на практике.
Развивающая:
-
формирование приемов логического мышления, умения анализировать;
-
развитие наблюдательности;
-
развитие памяти, концентрации.
Воспитательные:
-
воспитание аккуратности;
-
воспитание привычки - доводить начатое до конца.
Предметные результаты: научиться: умножать одночлен на многочлен; формулировать алгоритм умножения одночлена на многочлен; приводить многочлен к стандартному виду.
Метапредметные результаты:
- представлять конкретное содержание и сообщать его в устной и письменной форме;
- вступать в диалог, а также участвовать в коллективном обсуждении проблем;
- умение аргументировать свою точку зрения, спорить и отстаивать свою позицию невраждебным для оппонентов образом;
- использование адекватных языковых средств для отображения в форме речевых высказываний своих чувств, мыслей, побуждений и иных составляющих внутреннего мира;
-речевое отображение (описание, объяснение) учеником содержания совершаемых действий в форме речевых значений с целью ориентировки (планирование, контроль, оценка) предметно-практической и иной деятельности как в форме громкой социализированной речи, так и в форме внутренней речи (внутреннего говорения в ходе усвоения новых умственных действий и понятий);
- поиск и выделение необходимой информации;
-умение структурировать знания;
- выдвижение гипотез и их обоснование;
-умение наблюдать;
-умение обобщать полученные данные;
-умение формулировать познавательную цель;
- осознанное управление своим поведением и деятельностью, направленной на достижение поставленных целей; способность преодолевать трудности и препятствия;
-осознают качество и уровень усвоения, оценивают достигнутый результат;
-понимают возможность различных точек зрения, не совпадающих с собственной.
Личностные результаты:
-проявляют дисциплинированность, трудолюбие и упорство в достижении поставленных целей;
-умение бескорыстно оказывать помощь своим сверстникам, находить с ними общий язык и общие интересы;
-развитие познавательных интересов, учебных мотивов.
Ход урока
1. Мотивация к учебной деятельности
-
Добрый день, уважаемые ребята! Меня зовут Зарема Джамалудиновна! И сегодня мне посчастливилось провести у вас урок алгебры! Разогреем свои ладошки, чтобы активизировать свои пальчики для работы. Поприветствуем наше многоуважаемое жюри! Садитесь!
- Ребята, сегодняшний урок я хочу начать со слов Героя Советского Союза, летчика-испытателя Валерия Чкалова:
Слайд 1.
«Математика – это полет!»
Валерий Чкалов
-
Как вы понимаете эту фразу? (Ответы детей.)
-
Как вы понимаете эти слова? (Ответы детей)
-
Правильно, ребята, сегодня мы совершим с вами полет в мир математики и совершим открытие. И поможет нам в этом прием «Герой и вершина». Посмотрите внимательно на экран, перед вами гора.
Слайд 2.
|
|
-
Ребята, кто такой герой? А кто герои сегодня на уроке? (Мы).
-
А что такое вершина? А что сегодня на уроке будет у нас вершиной? (Новые знания, новая тема, цели урока).
Слайд 3-4.
-
У каждого на парте эскиз этой горы с пустыми прямоугольниками. Ваша задача, заполнить эти прямоугольники ключевыми понятиями в течение урока – это ранее вами накопленные знания, и добраться до вершины – то есть, приобретение сегодня вами новых знаний.
2. Актуализация опорных знаний и фиксация затруднения при выполнении заданий
─ Итак, ребята в путь!
Внимательно посмотрите на следующий слайд и выберите на нем понятия, с которыми вы можете связать прошлые уроки.
Слайд 5-6.
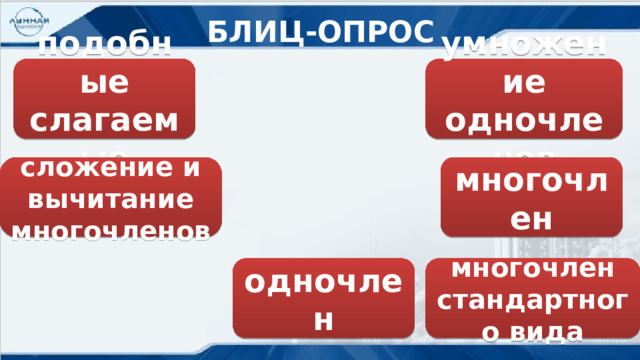
На экран выведены следующие понятия: подобные слагаемые, система уравнений, одночлен, многочлен, проценты, треугольник, сложение и вычитание многочленов, смешанное число, статистика, умножение одночленов, стандартный вид многочлена.
─ Понятия, которые вы считаете ключевыми, выписываем и заполняем пустые прямоугольники на горе.
─Итак, давайте проведем «Блиц-опрос». Называем ключевое понятие и даем ему определение.
Учитель поднимает по одному ученику, который тянет руку и хочет ответить, и по мере заполнения горы каждым учеником, он заполняет гору на доске по заранее заготовленным элементам ключевых понятий.
─Все вспомнили ключевые понятия, необходимые нам сегодня? Тогда полетели дальше? (Да)
─ Внимание на следующий слайд.
Слайд 7.
| Задание №1. Выполняя задания на преобразование выражений, содержащих степени ученик допустил ошибки. Ответить на вопрос - какое свойство забыл ученик и исправить его ошибки, а) 23 *27 = 221 б) 23 * 27 = 410 в) 23 *27 = 421
|
Учитель вызывает одного ученика к доске, он исправляет эти ошибки, озвучивает свойство умножения степеней с одинаковыми основаниями и формулирует правило. После, на том же слайде появляются правильные ответы, и дети сверяют свои ответы с ответами на слайде.
Слайд 8.
| Задание №1. Умножение степеней с одинаковыми основаниями: 23 * 27 = 23+7 = 210 |
─Молодцы, ребята! Справились с этим заданием, вспомнили одно из важнейших свойств степеней – умножение степеней с одинаковыми основаниями. Давайте это свойство запишем в пустой прямоугольник, а я отмечу на своей горе, так как знание этого свойства очень важно при открытии нового знания.
─Теперь, опираясь на наши ключевые понятия и на все изложенное нами, выполните следующее практическое задание.
Слайд 9.
| Задание №2. Найти произведение одночленов:
|
Слайд 10. Ответы для самопроверки:
| Задание №2. Найти произведение одночленов:
|
Слайд 11.
| Задание №3 Выполнить практическую работу: 2. ( -3n3+2n) –(7n2-- 5n3 _11n) = 3. 3а·(а2 + 2а - 2) = |
Слайд 12. Ответы для самопроверки.
| Задание №3 Выполнить практическую работу: 2. ( -3n3+2n) –(7n2-- 5n3 _11n) = 2n3-7n2+13n
3. 3а·(а2 + 2а - 2) =
|
─ Какие ключевые понятия вы использовали при ответе при выполнении этих заданий?
При решении последнего примера у учащихся появляются вопросы. На выполнение заданий учитель выделяет 3 минуты. Учитель поднимает с места по одному ученику и записывает правильные ответы на доске, после на том же слайде появляются правильные ответы, и дети выполняют самопроверку).
(Заранее заготовленные элементы крепятся на гору, и теперь дети видят соответствие, и материал еще более освежается в их памяти.
При выполнении последнего задания у учащихся появляются сомнения и вопросы. Такое задание они раньше не выполняли. Появляется проблема.
─ Ребята, что у вас не получается выполнить? ( Не можем выполнить умножение, не уверены, правильно ли).
─ Что необходимо сделать дальше? (Надо выяснить причину возникшего затруднения)
─ А какое задание вы здесь должны были выполнить? (Умножить одночлен на многочлен)
─ А как вы думаете, почему у вас не получается? (Не знаем правило)
3. Решение проблемы, построение выхода их затруднения.
─ Ребята, как думаете, какова тема нашего сегодняшнего урока? (Умножение одночлена на многочлен).
На экране появляется следующий слайд с темой урока.
Слайд 13.
|
Тема урока:
УМНОЖЕНИЕ ОДНОЧЛЕНА НА МНОГОЧЛЕН
|
А также тему урока учитель вывешивает на вершине горы, и дети тоже записывают в свои рабочие листы.
─ Какую цель вы перед собой сегодня поставите? (научиться умножать одночлен на многочлен, вывести алгоритм умножения одночлена на многочлен)
На экране появляется цель урока.
Слайд 14.
|
Цели урока:
1. Научиться умножать одночлен на многочлен; 2. Вывести алгоритм умножения одночлена на многочлен; 3. Научиться применять этот алгоритм на практике.
|
─ Как вы думаете, что поможет нам в достижении целей? Каков план достижения вершины горы? Какое свойство нам необходимо вспомнить? Составим план достижения цели.
Слайд 15.
На экране появляется слайд с информацией, содержащий план достижения цели.
|
План достижения цели (вершины горы): 1. Вспомнить распределительное свойство умножения; 2. Выработать алгоритм умножения одночлена на многочлен; 3. Применить его при решении заданий.
Открывать новые знания вам поможет умение использовать информацию, наблюдать, анализировать, делать выводы и быть внимательным.
|
Учитель задает наводящие вопросы:
─ Вспомним, как записывается распределительное свойство умножения относительно сложения, а для этого окунемся в 5 класс.
- Сейчас на экране его алгебраическая интерпретация и геометрическая.
Слайд 16.
| a · (b + c) = ab + ac - буквенная и
|
─ И это свойство выводим на нашу гору, так как это свойство является одним из ключевых понятий при открытии новых знаний.
- Мы практически у вершины, но цель еще не достигнута. Что еще осталось нам сделать? (Выработать алгоритм умножения одночлена на многочлен и научиться применять этот алгоритм при решении заданий)
Также учитель вывешивает на доске заранее заготовленный макет с записью распределительного свойства умножения.
4. Физминутка.
─ А теперь, чтобы наша дальнейшая работа была такой же активной и продуктивной, давайте разбудим наши спящие нейронные клетки с помощью нейрогимнастики. Встали, разомкнули плечи, потерли ладошки. Теперь сели и повторяйте за мной. Главное, упражнения выполнять одновременно двумя руками. Одновременно. Только в этом случае ваш мозг обречен на активность и плодотворность. Каждое упражнение выполняем по одной минуте.
Слайд 17.
|
Нейрогимнастика 1. Первое упражнение – здороваемся с большим пальцем левой и правой руки; 2. Второе упражнение – «заяц – пистолет».
|
5. Первичное закрепление с проговариванием вслух.
─ Итак, полетели дальше к нашей вершине. Выработать алгоритм и сформулировать его нам поможет упражнение «Гусеница»
Слайд 18.
| Задание №4 Упражнение «Гусеница»
умножитьэтотодночленнакаждыйчленмногочленаполученныепроизведениясложитьчтобыумножитьодночленнамногочленнужно
|
После нескольких попыток у некоторых учеников получается выделить предложения и сформулировать алгоритм умножения одночлена на многочлен. После чего на слайде появляется верная формулировка алгоритма.
Слайд 19.
| Алгоритм умножения одночлена на многочлен:
Чтобы умножить одночлен на многочлен, нужно 1. Умножить этот одночлен на каждый член многочлена; 2. Полученные произведения сложить.
|
Ученики запоминают и проговаривают правило. Двух учеников учитель поднимает и спрашивает формулировку. Каждому ученику учитель раздает этот алгоритм, и сам вывешивает заранее заготовленный элемент на гору.
─ Теперь вернемся к заданию, которое вызвало у нас затруднение, и попытаемся его решить, применив алгоритм.
Учитель показывает решение этого задания на слайде , комментируя каждое действие, интересуясь, поняли ученики его решение или нет.
Слайд 20.
|
3а · (а2 + 2а - 2)= 3a3 + 6a2 - 6а
|
─ Итак, ребята, теперь задание по рядам. Какой ряд выполнит быстро и правильно, получит от меня подарок в конце урока.
Слайд 21.
Задание №5. Выполнить умножение одночлена на многочлен с помощью алгоритма.
|
С каждого ряда один ученик выходит к доске и решает, потом сверяем на слайде с правильными ответами.
Слайд 22.
|
6. Самостоятельная работа с самопроверкой.
─ А теперь я предлагаю вам поработать самостоятельно, чтобы вы могли проверить себя с использованием эталона, который у вас на экране.
Слайд 23.
| Задание №6 Преобразуйте выражение: 1в. 3n4· (n2 + 2n – 4) = 2в. - 2m3· (3m - 2m2 + m3) =
|
Ответы появляются на слайде после решения детьми. Каждый ученик честно проверяет задание другого варианта, и справедливо его оценивает.
Слайд 24.
| Задание №6 Преобразуйте выражение: 1в. 3n4· (n2 + 2n – 4) = 3n7+6n5-12n4 2в. - 2m3· (3m - 2m2 + m3 ) = - 6m4+4m5-2m6
|
-
У кого задание вызвало затруднение? (Ответы детей)
-
Почему у вас возникли затруднения? (Ответы детей)
-
Что вам необходимо сделать, чтобы в дальнейшем не допускать ошибок? (Ответы детей)
-
Кому удалось справиться с заданием без ошибок? (Ответы детей
-
Ребята, вы ничего не заметили? (На доске ошибка)
Дети обнаруживают ошибку в решении первого примера, которое появилось на экране, исправляют ее.
Слайд 25.
| 3n4· (n2 + 2n – 4) = 3n6+6n5-12n4
|
7. Включение в систему знаний и повторение
-
Сможете ли вы в дальнейшем использовать открытые знания?
-
Где могут пригодиться полученные знания?
Слайд 26.
|
|
Слайд 27.
| Задание №7: Реши ОГЭ:
|
Слайд 28. (для проверки)
| Задание №7: Реши ОГЭ:
|
8. Рефлексия деятельности на уроке.
– Итак, вернемся к эпиграфу урока.
─ Совершили ли вы полет на уроке математики? (Да…
─ При совершении полета на что мы опирались? (Известные знания…эпиграф к уроку…гора…
– Открыли вы сегодня новые знания?(Да
– Какие цели вы поставили вначале урока?(Ответы детей…
– Достигли вы этих целей?(Да…
─ Проанализируйте свою работу на уроке, заполнив карточки, которые лежат у вас на партах, и для обратной связи сдайте мне их.
Слайд 29.
|
| Рефлексия (утверждения) | Да, Нет |
| 1. | Сегодня на уроке у меня все получилось, я не допускал(а) ошибок, у меня не было затруднений в выполнении заданий |
|
| 2. | Я допустил(а) ошибки … |
|
| 3. | Я исправил(а) свои ошибки с помощью… |
|
| 4. | Мне необходимо поработать над … |
|
| 5. | Какую оценку вы себе поставите… |
|
9. Домашнее задание
Слайд 30.
-
П.27. Преобразование произведения одночлена и многочлена. Стр.135.
-
Для тех у кого есть вопросы – повторить свойства степеней, приведение одночлена и многочлена к стандартному виду.
-
Выполнить: № 614 (а-в), 616 (а, б) (кто допустил ошибки)
-
№ 614 (г-е), 616 (в, г) (кто не допустил ошибок)
─ Урок окончен! Спасибо! До встречи!
Слайд 31.
| Спасибо за урок!
«Я совершал много ошибок, но я продолжал идти. Просто идите!». Рене Декарт
|
5

 Получите свидетельство
Получите свидетельство Вход
Вход



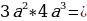



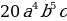


















































 Материалы к открытому уроку по алгебре "Умножение одночлена на многочлен" (810.35 KB)
Материалы к открытому уроку по алгебре "Умножение одночлена на многочлен" (810.35 KB)
 0
0 127
127 2
2 Нравится
0
Нравится
0


