Аннотация.
Известно, что нормальные подгруппы любой группы образует модулярную решетку. В связи с этим в данной заметке построены решетки нормальных подгрупп группы симметрии треугольника и квадрата.
Группой называется множество G элементов произвольной природы, на котором задана бинарная операция такая, что выполняются следующие условия:
1) ассоциативность: (ab)c=a(bc) для любых элементов a, b, c из G;
2) в G существует такой элемент e, что ea=ae=a для любого элемента a из G, такой элемент e называется единицей группы G;
3) для любого элемента a из G существует такой элемент a-1 из G, что a*a-1=a-1*a=e, такой a-1 элемент называется обратным к элементу a.
Алгебра (L; ⋀, ⋁) называется решеткой, если L непустое множество, а ⋀ и ⋁- бинарные операции на L, которые идемпотентны, коммутативны, ассоциативны и удовлетворяют двум тождествам поглащения.
Связь между группой и решеткой непосредственно видна из следующей теоремы.
Теорема 1[1,2]. Нормальные подгруппы любой группы G образуют модулярную решетку.
Подгруппа некоторой группы называется нормальной подгруппой, если она переходит в себя при всех внутренних автоморфизмах группы. Другими словами, подгруппа N группы G называется нормальной подгруппой в G, если для любого элемента a из N и любого g из G элемент g*a*g-1 содержится в N.
1. Решетка нормальных подгрупп правильного треугольника
Пусть А, В, С – вершины равностороннего треугольника АВС (рис. 1 а). Повернем треугольник вокруг его центра О на 1200 в направлении, указанном стрелкой. Тогда вершина А перейдет в вершину В, В в С, С в А. Таким образом, треугольник совместится со своим первоначальным положением (если не учитывать названия вершин), то есть поворот на 1200 вокруг точки О является преобразованием, переводящим данный треугольник в себя. Обозначим это преобразование через а.
Его можно записать в виде a=(A B C, BCA) где в верхней строчке перечислены все вершины треугольника, а нижняя строчка показывает, куда каждая из них переходит. А поворот на 2400,обозначим это преобразование через b, тогда b=(A B C,CAB). Имеется еще одно преобразование, переводящее треугольник в себя, отличное от a и b- это поворот на 00. Обозначим это преобразование через е, тогда e=(A bB C, A B C)
Можно составить таблицу умножения, где каждая строка, а также каждый столбец соответствует некоторому вращению, переводящему треугольник АВС в себя. На пересечении строки, соответствующей преобразованию g1, и столбца, соответствующего преобразованию g2, мы будем ставить преобразование, равное g1*g2. Так, например, в выделенную клетку таблицы 1 мы должны поставить преобразование a*b, которое получится, если сначала повернуть треугольник на 2400, а затем еще на 1200.

Следовательно, a*b – поворот на 3600, то есть совпадает с е. Тот же результат мы получим, если будем рассуждать следующим образом: преобразование b переводит вершину А в С, а преобразование а переводит вершину С в А. Таким образом, преобразование переводит вершину А в А. Точно так же можно получить, что вершина В переходит в В, а С переходит в С. Отсюда, a*b=(A B C? A B C), то есть a*b=e.
Любое преобразование некоторой фигуры в себя, сохраняющее расстояние между всеми ее точками, называется симметрией данной фигуры. Так, рассмотренные выше, вращения равностороннего треугольника являются его симметриями.
Кроме вращений, у равностороннего треугльника имеется еще три симметрии, а именно, отражение относительно осей l1, l2 и l3 (рис 1 б). Эти преобразования мы обозначим соответственно c, d, f так, что c=(A b C, A C B ), d=(A B C, C B A), f=(A B C, B, A C) .
Здесь можно по-разному понимать композицию двух преобразований. Рассмотрим, например, композицию преобразования c*d. Можно считать, что при выполнении преобразования d ось l1 переходит в новое положение (а именно, в положение старой оси l3), и после этого преобразование с рассматривать как отражение относительно нового положения оси l1 (то есть относительно старой оси l3). С другой стороны, можно считать, что они не связаны жестко с фигурой и не преобразуются вместе с ней и, следовательно, в рассматриваемом примере после выполнения преобразования преобразование с должно выполняться как отражение относительно старой оси l1. Именно так мы и будем рассматривать в дальнейшем композицию преобразований.
При таком подходе оказывается справедливыми рассуждения о вершинах фигуры, такие рассуждения удобно использовать для вычисления композиций преобразований.
Пусть некоторое множество преобразований G обладает следующими свойствами:
1) если преобразование g1 и g2 содержатся в G, то и их произведение g3=g1g2 содержатся в G;
2) если преобразование g содержатся в G, то и обратное ему преобразование g-1 содержатся в G.
Тогда такое множество преобразований G будем называть группой преобразований.
Нетрудно проверить, что множество преобразований представленных выше G=(e, a, b, c, d, f) с таблицей умножения является группой преобразований и называется группой симметрии треугольника.
Теперь находим все подгруппы из GΔ, а затем из них выделим только нормальные подгруппы. Непосредственная проверка показывает, что в GΔ имеются следующие подгруппы: подгруппа вращений (a, b, e), 3 подгруппы отражений относительно высот: (e,c), (e,d), (e,f), две тривиальные подгруппы: (e) и вся группа GΔ. Далее вспомним критерия нормальности подгруппы:
Теорема 2[3]. Подгруппа N группы G является нормальной подгруппой тогда и только тогда, когда левое и правое разложения группы G по подгруппе N совпадают.
Результаты применения теоремы 2 показывают, что среди выше указанных подгрупп из нормальными подгруппами являются трое: (e), (e, a, b) и вся группа GΔ (рис 1 в).
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



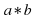 такая, что выполняются следующие условия:
такая, что выполняются следующие условия: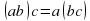 для любых элементов a, b, c из G;
для любых элементов a, b, c из G;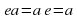 для любого элемента a из G, такой элемент e называется единицей группы G;
для любого элемента a из G, такой элемент e называется единицей группы G;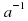 из G, что
из G, что 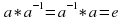 , такой элемент
, такой элемент 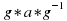 содержится в N.
содержится в N.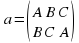 , где в верхней строчке перечислены все вершины треугольника, а нижняя строчка показывает, куда каждая из них переходит. А поворот на 2400,обозначим это преобразование через b, тогда
, где в верхней строчке перечислены все вершины треугольника, а нижняя строчка показывает, куда каждая из них переходит. А поворот на 2400,обозначим это преобразование через b, тогда 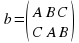 . Имеется еще одно преобразование, переводящее треугольник в себя, отличное от a и b- это поворот на 00. Обозначим это преобразование через е, тогда
. Имеется еще одно преобразование, переводящее треугольник в себя, отличное от a и b- это поворот на 00. Обозначим это преобразование через е, тогда 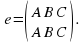
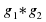 . Так, например, в выделенную клетку таблицы 1 мы должны поставить преобразование
. Так, например, в выделенную клетку таблицы 1 мы должны поставить преобразование 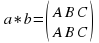 , то есть
, то есть 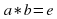 .
.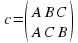 ,
, 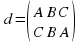 ,
, 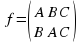 .
. 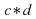 . Можно считать, что при выполнении преобразования d ось l1 переходит в новое положение (а именно, в положение старой оси l3), и после этого преобразование с рассматривать как отражение относительно нового положения оси l1 (то есть относительно старой оси l3). С другой стороны, можно считать, что они не связаны жестко с фигурой и не преобразуются вместе с ней и, следовательно, в рассматриваемом примере после выполнения преобразования
. Можно считать, что при выполнении преобразования d ось l1 переходит в новое положение (а именно, в положение старой оси l3), и после этого преобразование с рассматривать как отражение относительно нового положения оси l1 (то есть относительно старой оси l3). С другой стороны, можно считать, что они не связаны жестко с фигурой и не преобразуются вместе с ней и, следовательно, в рассматриваемом примере после выполнения преобразования 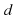 преобразование с должно выполняться как отражение относительно старой оси l1. Именно так мы и будем рассматривать в дальнейшем композицию преобразований.
преобразование с должно выполняться как отражение относительно старой оси l1. Именно так мы и будем рассматривать в дальнейшем композицию преобразований.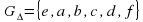 с таблицей умножения является группой преобразований и называется группой симметрии треугольника.
с таблицей умножения является группой преобразований и называется группой симметрии треугольника.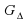 , а затем из них выделим только нормальные подгруппы. Непосредственная проверка показывает, что в
, а затем из них выделим только нормальные подгруппы. Непосредственная проверка показывает, что в 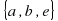 , 3 подгруппы отражений относительно высот:
, 3 подгруппы отражений относительно высот: 








 Материал по математике "Решетки нормальных подгрупп правильного треугольника и квадрата" (0.34 MB)
Материал по математике "Решетки нормальных подгрупп правильного треугольника и квадрата" (0.34 MB)
 0
0 472
472 13
13 Нравится
0
Нравится
0


