Организация восприятия учебного материала школьниками с разным уровнем обученности на уроках математики
План:
1. Введение.
2. Теоретическая часть:
- характеристика групп учащихся с учетом индивидуальных особенностей и уровня сформированности их умений.
3. Практическая часть:
-формирование познавательного интереса школьников;
-основа учебной математической деятельности: синтез и анализ;
-чертежи и рисунки, как эффективное средство формирования у учащихся умений подмечать закономерности на основе наблюдений, преобразований, сопоставлений;
-использование классной доски на уроках математики.
4. Вывод.
5. Литература.
Ориентация на личность ученика требует, чтобы дифференциация обучения математике учитывала потребности всех школьников - не только сильных, но и тех, кому этот предмет дается с трудом или чьи интересы лежат в других областях.
Получать удовольствие от занятий математикой ребята смогут лишь при условии когда материал будет доступен ему в той степени, в какой он пожелает. В противном случае один ученик будет учиться налегке, не напрягаясь, другой - пытаясь осилить непосильное. Первый из них не найдет применения имеющимся способностям и не разовьет потенциальные, второй будет чувствовать постоянное унижение, на каждом шагу ощущать собственную неполноценность, умственную убогость, что поведет к отвращению от математики.
Учитывая индивидуальные особенности каждого учащегося всех ребят в соответствии с уровнем сформированности их умений по решению задач можно разбить на три группы.
Учащиеся первой группы имеют пробелы в знаниях программного материала, искажают содержание теорем в применении их к решению задач, самостоятельно могут решать задачи в один-два шага, решение более сложных задач начинают со слепых проб, не могут найти связи между данными и искомыми величинами, часто пропускают обоснования гипотез и не понимают необходимости их проведения, не видят существенных зависимостей и ключевых моментов в решении задач.
Эта общая характеристика не исключает различных индивидуальных особенностей учащихся. Здесь могут быть учащиеся, имеющие пробелы в знаниях и отставание в развитии из-за частых пропусков уроков по болезни, в силу систематически плохой подготовки к урокам. Вместе с тем эту группу составляют учащиеся, относящиеся разным уровням обучаемости. Те из них, кто имеет высокий уровень обучаемости, после ликвидации пробелов в знаниях и при соответствующем обучении обычно быстро переходят на более высокие уровни развития.
Учащиеся второй группы имеют достаточные знания программного материала, могут применять их при решении стандартных задач. Затрудняются при переходе к решению задач нового типа, но, овладев методами их решения, справляются с решением аналогичных задач; не справляются самостоятельно с решением сложных задач (нетиповых) задач. У них не сформированы эвристические приемы мышления, они с большим трудом могут сформулировать гипотезу относительно конечной цели и промежуточных подцелей в процессе поиска решения задачи.
Третью группу составляют учащиеся, которые могут сводить сложную задачу к цепочке простых подзадач, выдвигать и обосновывать гипотезы в процессе поиска решения задач, переносить прежние знания в новые условия. Они быстро и легко обобщают методы решения классов однотипных задач, совершенно отчетливо выделяют ключевую подзадачу в решенной, могут сформулировать ее в ходе поиска решения самостоятельно или с небольшой помощью учителя, находят несколько способов решения одной задачи, используют различные приемы, но обычно неосознанно.
Знание уровня сформированности у школьников умений по решению задач позволяет при подготовке к уроку заранее спланировать все виды дифференцированных воздействий, подобрать соответствующие задачи и продумать формы помощи для каждой группы учащихся, ориентируясь на зону ближайшего их развития.
При формировании познавательного интереса, познавательной активности учащихся я стараюсь использовать различные средства, приемы в зависимости от возраста ребят, материала, темы, особенностей класса, категории школьников ( хорошо успевающих, средних и слабоуспевающих ).
Труднее всего формировать интерес к предмету у слабоуспевающих учащихся. К арсеналу, помогающему формировать устойчивый интерес к предмету отношу содержание изучаемого материала, умелое сочетание форм и методов работы на уроке, моральный климат в отношениях как учителя к учащимся данного класса, так и между учащимися внутри классного коллектива.
Как же привлечь внимание всех учащихся к поставленному заданию? Одним из путей может быть такой: анализируем условие задачи и коллективно намечаем ход решения; когда всему классу понятен ход решения, предлагаю записать решение на доске слабоуспевающему ученику. Или работу можно построить так: предлагаю кратко записать условие задачи слабоуспевающему ученику, затем организовываю коллективный поиск решения задачи. Это способствует осознанию условия задачи слабым учеником и приобщает его к активной познавательной деятельности на уроке.
Часто причина плохого выполнения письменных работ контролирующего характера кроется в отсутствии у школьников умения осуществлять самоконтроль. В таких случаях я использую задания, обучающие приемам контроля, задания, оценивающие контроль и самоконтроль, и задания, "провоцирующие" учащихся на контроль своих и чужих действий. Интерес к самоконтролю может вызвать такая форма проверки кратковременных самостоятельных работ. После истечения времени, отведенного на выполнение самостоятельного задания, предлагаю учащимся обменяться тетрадями и проверить работу товарища. Нравиться ребятам, когда даю задание на исправление преднамеренно сделанных ошибок в решении, на восстановление частично стертых записей. Недописанная фраза, недорешенная задача, недосказанное условие в задаче стимулируют работу учащихся. Любят ребята всех возрастов, когда уроки оживлены задачами- шутками, задачами на внимание.
Это не только воспитывает внимание, но и вызывает познавательный интерес к содержанию учебного материала. Такая форма работы учит ребят не только проверять, но и качественно выполнять задания, предложенные на самостоятельных и контрольных работах.
Учащиеся подросткового возраста, а тем более слабоуспевающие из них, особенно быстро устают от длительной, однообразной умственной работы. Усталость - одна из причин падения интереса и внимания к учению. Уменьшить усталость учащихся от выполнения однообразных упражнений вычислительного характера можно с помощью игровых ситуаций, разнообразных математических соревнований. Например, при закреплении материала на все действия с десятичными дробями ( 5 класс ) провожу эстафеты по группам или между мальчиками и девочками отдельных групп.
Даю задание: выполнить действия:
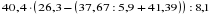 .
.
Представитель от каждой группы, выполнив на доске одно действие, передает эстафету своему товарищу. Члены группы имеют право на исправление ошибок во время эстафеты, но у доски может находиться не более одного участника каждой команды.
Такая игра способствует не только формированию знаний и умений, быстроты и гибкости мышления, но и воспитывает чувство коллективизма. Игра заставляет всех без исключения учащихся повторять материал, в противном случае он может подвести команду. Для того чтобы слабоуспевающий ученик чувствовал себя полноправным членом коллектива, стараюсь создать доброжелательную обстановку в группе, своевременно помочь отстающим.
Слабоуспевающие учащиеся трудно воспринимают учебный материал, после объяснения не всё понимают сразу, им нужно затратить дома намного больше времени для уяснения нового материала, чем хорошо успевающему ученику. Плохая оценка, поставленная такому ученику, может вызвать негативное отношение к предмету и неприязнь к самому учителю, а необоснованное обвинение в лени - скомпроментировать ученика перед классом. Поэтому оценить ответы слабоуспевающих учащихся баллом стараюсь на последних уроках изучения какой-либо темы, а на первых уроках ограничиваюсь краткой, доброжелательной словесной характеристикой ответа.
Не всегда ученик, читая пункт учебника, в состоянии выделить главные объекты познания. Для формирования умения выделить главное использую не только объявление темы урока, но и запись на доске кратких вопросов, ответы на которые предполагаем получить на уроке. Перечень таких вопросов помогает не только изучению нового материала, но и подведению итогов на уроке. После изучения какого-либо правила предлагаю учащимся привести примеры, для решения которых можно его применить. Обычно при этом сначала находятся лишь один-два человека, желающих ответить, а затем почти все учащиеся хотят привести свой пример. Такие вопросы способствуют лучшему пониманию изучаемого материала.
Главным элементом учебной деятельности является осмысление цели, которое самым тесным образом связано с познавательным интересом. При постановке цели урока я стараюсь найти такой прием, который бы возбуждал у учеников интерес и желание познать новое. Совсем по-другому воспринимается цель урока, когда учащиеся сами становятся исследователями той или иной проблемы, сами убеждаются в необходимости изучения темы.
Так, при изучении деления десятичных дробей на 10; 100; 1000 и т.д. (5 класс) я не формулирую тему урока сразу, а предлагаю ребятам следующую систему заданий:
1. - Попробуйте догадаться, как можно быстро выполнить деление:
138,5 : 10; 138,5 : 100; 138,5 : 1000.
2. - Объясните, почему 8,45 : 100 = 0,0845. Если не можете, то прочитайте в учебнике о делении десятичных дробей на 10; 100; 1000 и т. д.
3. - Придумайте сами похожий пример и предложите его решить товарищу по парте.
После выполнения такой работы цель урока будет понятна всем ученикам, и усвоение темы пойдет быстрее и качественнее.
Убедительнее воспринимается учащимися цель деятельности, когда они видят, как связаны новые знания с явлениями окружающей жизни.
Следующим элементом учебной работы является формирование потребности в умениях и навыках. Это достигаю разнообразными приемами, активизирующими познавательный интерес учащихся.
Очень любят школьники на уроках математики встречаться со сказочными героями, особенно с Незнайкой, который старается учиться хорошо, но у него не всегда все получается, и поэтому ему необходимо помочь, например, в таких заданиях (5 класс):
" Жители Цветочного города попросили Знайку и Незнайку вычислить значение выражения 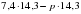 при р = 6,4. Незнайка начал решать так:
при р = 6,4. Незнайка начал решать так:
А Знайка внимательно посмотрел на пример и сразу записал ответ. Незнайка очень удивился! Ребята, а вы смогли бы решить так быстро?"
Задания такого рода помогают ученику понять, зачем ему нужны те или иные умения и навыки, тем самым формируется потребность в них. С этим элементом учебной деятельности тесно связана выработка умений организовать свои действия в единую систему. Для чего необходима четкая последовательность заданий, отрабатывающая каждый шаг.
В качестве примера возьму последовательность заданий при умножении десятичных дробей (5 класс).
Сначала даю упражнения, помогающие вспомнить все трудные ситуации, возникающие при умножении натуральных чисел:
1. - Незнайка, выполняя примеры, допустил ошибки. Помогите Незнайке отыскать их.
Посоветуйте ему, где нужно быть осторожным при умножении.
2. - Выполните действия и сравните результаты с данными ответами:
| 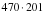
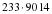
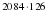
| Ответы: 94470; 2100262; 262284. |
3. - Придумайте сами 2 - 3 примера на умножение.
4. - Дополнительное задание: вместо ( * ) поставьте нужную цифру:
После выполнения этих заданий перехожу к обычным тренировочным упражнениям на умножение десятичных дробей, разъясняя отдельно каждый шаг вычислений:
1. - Перемножьте числа: 241 * 38; 2,41 * 38; 2,41 * 3,8.
2. - Выполните умножение: а) 33 * 2; г) 3,3 * 2; ж) 33 * 0,2;
б) 3,3 * 0,2; д) 0,33 * 0,2; з) 3,3 * 0,02;
в) 0,33 * 0,02; е) 0,2 * 0,33; и) 2 * 3,3 .
3. - Ответьте на вопросы к предыдущему заданию: - Почему в примерах д), е) и г), и) одинаковые ответы? - Объясните, как выполняется умножение, если один из множителей является натуральным числом. - Можно ли воспользоваться правилом умножения десятичных дробей при умножении натуральных чисел? - Как следует поступать, если в произведении получится меньше цифр, чем содержится после запятой в обоих множителях?
4. - Зная, что 632 * 38 = 24016, найдите значение произведений: 63,2 * 38; 6,32 * 3,8; 63,2 * 0,38; 6,32 * 38; 63,2 * 3,8; 632 * 0,38.
5.- Найдите значения произведений: 1,13 * 0,25; 423 * 6,7; 3,14 * 25,1; 0,1245 * 200.
Работа со слабыми показывает, что иногда они не воспринимают объяснение нового материала, не могут решить простейших примеров по новой и предыдущим темам. В таких случаях я использую обучающие карточки. Обучающая карточка состоит из чередования трех блоков: 1) Опорная формула, написанная цветными чернилами; 2) Решенные примеры; 3) Р. С. - реши сам. Ученик получает чистый лист бумаги, на котором пишет свою фамилию. Сверху накладывает обучающую карточку. Знакомится с формулой и разобранными примерами затем решает сам. Для проверки сдает нижний лист, а карточку передает следующему ученику.
Часто ученик ( особенно не имеющий склонностей к математике ) не понимает, что следует делать, когда ему даешь те или иные задания: "докажи", "подумай", "выдели главное", "прочти внимательно", "проанализируй" и т. п. Особая сложность заключается в том, что деятельность ученика в таких случаях не адекватна его возможностям и он не понимает сути этой работы. Так в 5 классе при изучении темы "Чтение и запись натуральных чисел" требуется выполнить в системе упражнений пять видов действий: - прочти следующие числа... - запиши числа цифрами... - запиши число в виде суммы разрядных слагаемых... - составь многозначное число... Про все эти действия в тексте пункта практически ничего не сказано.
Поэтому основу учебной математической деятельности составляют два приема: синтез и анализ, которые характеризуют и любую другую деятельность человека. На их базе формируются уже более тонкие виды деятельности: анализ через синтез и синтез через анализ. Т. о. целесообразно систематически, целенаправленно и дифференцированно формировать умения учащихся использовать в своей работе синтез и анализ. Стратегия такого обучения в общих чертах выглядит следующим образом. Синтез: Пусть рассматривается какое-то математическое понятие, задача или теорема. Учащимся предлагаю следующие вопросы: - Что мы знаем про указанное понятие (про данные в задаче или теореме объекты)? - Какими свойствами оно (они) обладают? - Какие следствия из имеющихся данных мы можем получить? Анализ: Допустим, в задаче требуется что-то доказать или построить, вычислить. В этом случае предлагаю учащимся ответить на следующий вопрос: " Какие факты для этого нужно знать?" (на первых этапах обучения понятия "необходимо" и "достаточно" целесообразно заменить простыми и понятными словами "нужно", "можно").
Каждая конкретная задача служит конкретным целям обучения, но основная ее цель - развитие творческого и математического мышления учащихся, повышение их интереса к математике. Этому способствуют, прежде всего, так называемые красивые задачи. В понятии "красивая задача" всегда есть элемент субъективизма. Тем не менее, понятие "изящное решение" задачи, "красивый вывод" и т. д. является в математике общепринятым.
Чтобы помочь школьникам осознать эстетику задачи, с первых уроков геометрии знакомлю учащихся с различными способами решения одной задачи, различными приемами доказательств одной и той же теоремы, например, теорема о сумме углов треугольника. Восприятие эстетической стороны задачи начинается у школьников с условия. Поэтому содержание условия должно вызывать интерес (тут важна и форма подачи условия и его занимательность).
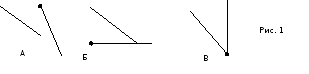
В геометрических задачах большую роль играет чертеж (достаточно вспомнить задачи о вычерчивании фигур одним росчерком, задачи на разрезание и др.) Чертеж должен соответствовать значению слова "красивый", т.е. "доставляющий наслаждение, приятный внешним видом, гармоничностью, стройностью". В школьном курсе геометрии выделяют три вида чертежей: - чертежи, иллюстрирующие содержание вводимого понятия; - чертежи, образно представляющие условие задачи или рассматриваемого математического предложения; - чертежи, иллюстрирующие преобразования геометрических фигур. Формируя у учащихся умение работать с чертежом, нужно помнить, что если ограничиваться стандартными чертежами, то школьники связывать формулируемое понятие только с фигурами определенного вида и положения. "Стандартный" чертеж вызывает у учащихся неверные ассоциации, в результате которых в содержание понятия вносятся мнимые признаки, являющиеся частными признаками демонстрируемой фигуры. Приведу примеры. Выполняя задание на распознавание углов некоторые учащиеся 7-ых классов называют углом лишь фигуру, изображенную на рис. 1Б. А фигуры на рис. 1А, В эти учащиеся не считают углами, т. к. часто видят только те изображения углов, которые аналогичны рис. 1Б.
| 
|
Бывают случаи, когда ребята считают смежными углы на рис. 2Б, но не относят к смежным углы на рис. 2А, В.
- "Какой из углов больше на рис. 3А, Б: угол 1 или угол 2?" На такой вопрос часто дается ошибочный ответ: " угол 1 больше угла 2".
Значит, у таких ребят не сформированы понятия о стороне угла, о величине угла и учащиеся пользуются житейскими представлениями, которые вступают в противоречие с геометрическими знаниями.
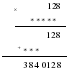
Эффективность формирования у учащихся понятий, которые можно представить наглядно, в значительной мере зависит от того, в каком виде произошло первое знакомство с ним, первый зрительный образ данного понятия. Поэтому в начале изучения понятия я показываю как можно больше чертежей, в которых варьируются несущественные признаки понятия. Для развития мышления учащихся формирую у них умение вычленять из элементов новые фигуры, не упомянутые в тексте условия задачи. Для формирования операции переосмысливания фигур использую задания такого рода: - Сколько отрезков изображено на рис. 4? - Сколько углов на рис. 5? - Назовите все треугольники и все четырехугольники на рис. 6.
| 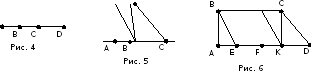
D А |
Чертежи и рисунки - эффективное средство формирования у учащихся подмечать закономерности на основе наблюдений, вычислений, преобразований, сопоставлений. Укажите лишние треугольники на рис. 7.
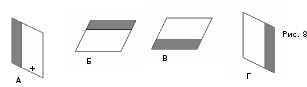
Здесь четыре тупоугольных и два не тупоугольных треугольника, следовательно треугольники "В, Д" можно считать лишними. Но в данном случае ответ может быть и другим. Например, только один треугольник "В" равносторонний, значит, он и лишний. Чертеж позволяет наглядно представить учащимся важную математическую идею или подвести их к осознанию неочевидного факта. На рис. 8 показано, как фигура перемещается по плоскости. Она последовательно занимает положения от "А" до "Г". Не вращая чертежа, отметьте положение крестика в случаях "Б, В, Г".
Это задание является пропедевтикой изучения понятия о движении (9 класс). - Разрежьте треугольник на рис. 9"А" так, чтобы из получившихся частей можно было сложить прямоугольник (ответ - рис. 9"Б").
- Трапецию на рис, 10А разрежьте на две части так, чтобы из них можно было сложить треугольник (ответ - рис. 10Б).
Эти два задания подготавливают учащихся к самостоятельному "открытию" формул для вычисления площади треугольника и трапеции (8 класс). Учащимся обычно свойственны переоценка роли чертежа и излишнее доверие ему. В результате при решении задач часто используются не те данные, работа с которыми ведет к успеху, а совсем другие, не нужные для данного этапа решения. При обучении решению геометрических задач я стараюсь следить за тем, чтобы формулировка задачи помогала учащимся сделать чертеж. В школьных учебниках текст, с помощью которого сформулирована задача или теорема, не всегда написан доступным, понятным языком. Как показывает практика, ученикам труднее всего даются такие тексты, в которых краткость достигается нанизыванием придаточных предложений или причастных оборотов. Например, одна и та же задача может быть сформулирована так: 1). Определите острый угол, если перпендикуляр, восставленный к его биссектрисе, образует с его сторонами два угла, из которых тупой угол вдвое больше острого угла. 2). Даны острый угол и его биссектриса. К биссектрисе восставлен перпендикуляр. Перпендикуляр образует со сторонами острого угла два угла, один из которых острый, а другой - тупой. Тупой угол вдвое больше острого. Определите острый угол. Во втором случае условие задачи сформулировано короткими фразами, основные мысли выражены простыми предложениями, данные приведены в виде прямых указаний с соблюдением такой последовательности, которая, по сути, отражает этапность построения чертежа. Поэтому во втором случае и чертеж построить легче.
Особое место в развитии мышления занимает обучение сравнению, в частности сравнению факта, выраженного словесно, с его интерпретацией на чертеже. Чертеж может служить опровержением какого-то общего высказывания. Учась опровергать неверные высказывания, школьники постепенно привыкают к доказательствам. Ниже приведу примеры трех заданий, которые нацеливают учащихся на поиск контр примеров. - Верно ли утверждение: " Любой четырехугольник, у которого диагонали взаимно перпендикулярны, является ромбом?" (рис. 11А) - Верно ли утверждение: " Любой четырехугольник, у которого два противолежащих угла прямые, является прямоугольником? " (рис. 11Б) - Изобразите на чертеже случай, для которого неверно высказывание: "Прямые называются параллельными, если они лежат в одной плоскости и не имеют ни одной общей точки."(пропущено указание на то, что речь идет о двух прямых) (рис. 11В).
| 
|
При изучении стереометриии в старших классах большое внимание обращаю на вычерчивание пространственных фигур. Понимание стереометрических чертежей весьма трудно дается учащимся из-за сугубой их условности: на чертеже искажаются величины углов, длины отрезков, пресекаются между собой линии, в действительности не имеющие общих точек, и т. п. Многие учащиеся со слабо развитым пространственным воображением весьма долгое время не в состоянии преодолеть эти трудности и ограничиваются лишь механическим воспроизведением по учебнику или с классной доски наиболее употребительных фигур, не сумев изобразить на чертеже условия какой-нибудь новой задачи. Поэтому с первых же шагов изучения геометрии я стараюсь сообщить учащимся элементы графической грамотности и строго слежу за технической доброкачественностью своих собственных чертежей на доске. При выполнении стереометрических чертежей использую следующие принципы: - проекция прямолинейного отрезка, параллельного плоскости проекций, сохраняет размеры и направление проектируемого отрезка независимо от расстояния последнего от плоскости проекций; - проекция прямолинейного отрезка, перпендикулярного к плоскости проекций, изображается в виде отрезка под углом 45 градусов к прямой, принятой за горизонтальную, причем длина этой проекции уменьшается вдвое по сравнению с длиной проектируемого отрезка. Например:
| 
|
- при изображении круглых тел круги, лежащие в плоскостях, непараллельных плоскости проекций, изображаю в виде эллипсов. Если плоскость круга расположена горизонтально, то большую ось эллипса располагают в направлении, принятом на чертеже за горизонтальное.
К этим правилам следует добавить несколько условных правил, определяющих вид линий различного назначения: - все части фигуры, данные по условию изображать линиями наибольшей толщины; - все вспомогательные линии, проводимые в ходе доказательства или решения, изображать линиями наименьшей толщины; - в пространственных фигурах невидимые части фигуры изображаются штриховыми линиями и тоньше, чем основные; - для изображения плоских сечений употребляется параллельная штриховка сплошными линиями наименьшей толщины; - равные отрезки и углы, как и в планиметрии обозначаются соответственно равным количеством штрихов или дуг.
Кроме этого всегда учитываю наиболее удачное расположение частей изображаемой фигуры.
Например: 1. Задача: В равнобедренном треугольнике основание и высота, проведенная к нему, равны 4 см. Данная точка находится на расстоянии 6 см от плоскости треугольника и на равных расстояниях от вершин. Найдите это расстояние.
|
| Построение чертежа: 1) изображаю плоскость, в которой лежит данный треугольник; 2) основание и высота должны быть проведены параллельно краям этой плоскости; 3) длина высоты СD и расстояние МО изображается без искажения, а длина основания АВ сократится вдвое. |
2. Задача: В треугольнике АВС угол С равен 90 градусов; СD перпендикуляр к плоскости этого треугольника. Точка D соединена с А и В. Определить площадь треугольника АDВ, если известно, что СА = 3 дм, ВС = 2 дм и СD = 1 дм.
| 
| Построение чертежа: 1) изображаю плоскость, в которой лежит треугольник АВС; 2) катеты треугольника АВС располагаю параллельно краям плоскости; 3) вершину С помещаю так, чтобы искомая площадь треугольника АВD не заслонялась другими частями фигуры. |
Эти основы графической культуры я прививаю к учащимся, развивая в них вкус и стремление к чертежу, в котором не только общий вид, но и каждая линия своим направлением, видом, толщиной отчетливо говорит о свойствах и взаимном расположении частей фигуры. При слабой восприимчивости учащихся, полезно бывает выделить некоторые части фигуры и вычертить их отдельно в дополнение к общему чертежу, помогая учащимся этим приемом разобраться в деталях той части, на которую обращается внимание. Такой прием иногда бывает необходим в начале курса планиметрии и часто неизбежен в курсе стереометрии. Так этим приемом я пользуюсь при доказательстве теоремы о двух перпендикулярах, выделяя каждую пару треугольников, например, АОD и А1OD, в которых одновременное условное изображение прямых углов при вершине О в виде тупого и острого углов часто приводит учащихся в недоумение и затрудняет усвоение теоремы.
Наконец, при рассмотрении многогранников - призм и пирамид - для исследования какого-нибудь элемента боковой грани или основания даю отдельно вид этой грани или основания в плоскости чертежа и, сделав на этом чертеже необходимое исследование, вношу полученные результаты на основной чертеж. Такой прием очень полезен при решении задач: помимо облегчения самого решения и предупреждения ошибочных суждений об относительных размерах сторон и углов изображенных на чертеже фигур этот прием помогает развитию пространственного воображения и конструктивных способностей учащихся. Задача: В правильной треугольной пирамиде боковое ребро, равное b, образует с основанием угол в 30 градусов. Найдите сторону основания.
|
| Начертив пирамиду по данным задачи, дополнительно рассматриваем вид основания сверху. Из дополнительного чертежа становится видно, что искомую сторону основания можно выразить через радиус круга ОС, а ОС легко выразить по основному чертежу через боковое ребро "в" из треугольника SОС. |
Часто перед учителем встают вопросы: - Что и когда записывать на доске? - Как именно вести записи? - Обязательно ли выполнять рисунки на доске с помощью чертежных инструментов или можно от руки? - Должен ли ученик после ответа стереть записанное им на доске или это делать необязательно? Требования при выполнении записей на доске одинаковы для учителя и учащихся. Каждая запись на классной доске должна быть грамотной, четкой, по возможности полной, пригодной для дальнейшего использования. Запись на доске обычно начинаю с верхнего левого угла и располагаю их как можно выше, особенно когда речь идет о доказательстве теоремы или решении задачи. Существенно сократить записываемый текст помогает математическая символика. Но пользуюсь я лишь общеупотребляемыми символами, не вводя своих, от которых ребятам позже придется отказаться. Отдельные части доказательства, решая на классной доске отделяю интервалом, чертой, заголовком или как-то иначе. Это облегчает восприятие. Не всегда целесообразно сразу сообщать ученикам тему урока и записывать ее на доске. Для активизации внимания учащихся иногда сначала создаю проблемную ситуацию, даю некоторые исторические сведения, связанные с темой урока, и только после этого записываю тему на доске. В большинстве случаев название темы урока сохраняю на протяжении всего урока.
Особого внимания заслуживают вопросы эффективного использования классной доски на уроках геометрии, т. к. здесь широко применяются математические символы, выполняется много рисунков. Объясняемый материал бывает разный - это и введение новых понятий, и изучение теорем, и вывод формул, и т.п. Поэтому записи на доске в каждом отдельном случае различны.
При введении новых геометрических понятий, как правило на доске выполняются рисунки иногда эти рисунки сочетаю с демонстрацией таблиц или моделей. Кроме рисунков при этом записываю термин для обозначения нового понятия, ставлю ударение в слове. К сожалению ребята ошибаются в написании таких слов, как "биссектриса", "перпендикуляр", "апофема", неверно делают ударение в словах "симметрия", "ось иксов", "гомотетия", "сегмент" и др.
Рисунок и записи к нему должны быть связаны между собой, образовывать удобную для восприятия систему. Например, при введении понятий "биссектриса, медиана, высота треугольника" (7 класс) записи и чертеж на доске оформляю так:
В некоторых случаях, чтобы сэкономить время на уроке, готовлю чертеж заранее. Но чаще бывает полезным сделать чертеж непосредственно на уроке, выполнить построение на глазах учеников, демонстрируя процесс "рождения" нового понятия. Приведу другой пример оформления записей на классной доске при изучении темы "Расстояние между точками" (8 класс). При этом можно выделить такие смысловые части: 1) рисунок, условие и требования; 2) вывод формулы для общего случая; 3) рассмотрение отдельных случаев.
|
|
A1(x1; y1) A2(x2; y2) A1A2 = d |
| d =  |
| .  ; ;  

 по т. Пифагора по т. Пифагора

| . а)  ; ;  
б)  ; ;  
в)  ; ;  
|
Такое выделение смысловых частей и обусловливает расположение записей на доске. Рассмотрим использование классной доски при доказательстве теорем. Изучение каждой теоремы, как правило, состоит из таких основных частей: - символическая запись условия теоремы и того, что требуется доказать; - дополнительные построения и операции, если таковые необходимы; - цепочка рассуждений; - вывод, который следует из приведенных рассуждений. В записи доказательства теоремы эти этапы целесообразно отделять (например, подзаголовками), а ход рассуждений в каждой части записывать по пунктам. Почти все теоремы школьного курса доказываются с помощью соответствующего рисунка. Его лучше располагать на доске слева, а справа записывать то, что дано и что требуется доказать. Чертеж на классной доске должен быть наглядным, удобным для дальнейшей работы с ним. Для этого при подготовке к уроку следует подумать, какие именно рисунки надо выполнить, как их расположить на доске, что выделить другим цветом. Можно и учащихся предупредить, как лучше сделать чертеж в тетради. Буквенные обозначения на рисунке не должны "наседать" на его линии и точки, их следует располагать рядом. Например, доказательство теоремы синусов (9 класс) можно расположить на доске следующим образом.
| Дано: ∆ ABC Доказать:  Доказательство: |
| случай.  острые острые
| случай.  тупой тупой
|
| 1) BD – высота |
| 2) Из  : : 
3) Из  : : 
| 2) Из  : : 


3) Из  : : 
|
| 4) Т. к. 5) Т. о.  ч. т. д. |
Записи доказательств теорем в начале изучения курса могут быть более детальными. В дальнейшем же можно перейти к их краткости. Решение задач на доказательство по сути не отличается от доказательства теорем, поэтому и записи здесь аналогичные. Запись решения задач на вычисление чаще всего состоит из таких частей: - дано; - найти; - решение; - ответ. Недоразумения здесь встречаются редко. Остановлюсь еще на задачах на построение. Задачи на построение учащиеся начинают решать в 7 классе. С известными этапами решения этих задач (анализ; построение; доказательство; исследование) стараюсь знакомить ребят постепенно. При решении несложных задач на построение рекомендую записывать только построение и доказательство. В более сложных случаях построению должны предшествовать рабочий рисунок и план построения, который следует из анализа. Анализ обычно проводим устно. Устно можно делать и исследование, если в этом есть необходимость.
Рассмотрю для примера такую задачу: « Построить прямоугольный треугольник по гипотенузе и высоте, опущенной из вершины прямого угла на гипотенузу». Её решение на классной доске можно оформить так:
| Дано: 
| Анализ: 
| Построение:
|
| Доказательство: ∆ ABC – искомый: AB = c (по построению) CK = h (по построению)  , т. к. AB – диаметр . , т. к. AB – диаметр .
|
В заключении можно сказать, что правильное использование классной доски - одно из важных средств повышения эффективности урока и улучшения восприятия изучаемого материала учащимися.
Т. о. организация восприятия учебного материала школьниками с учетом их уровня обученности на уроках математики показала, что для ребят нарушаются стереотипы, сравнивая и сопоставляя, они лучше замечают разницу в изучаемых понятиях, умеют выделять главное, в большинстве случаев не испытывают затруднений при построении чертежей, могут сформулировать условие задачи более понятно для слабого ученика. А все это приводит к повышению эффективности урока и улучшению качества знаний учащихся, воспитывает у них более заинтересованное и сознательное отношение к процессу обучения.
Литература
1. Ковалева Т. М. " Игра и учебная деятельность ".
2. Кухарь А. В. " Некоторые пути формирования познавательного интереса ".
3. Овечкина О. И. " Приемы активизации познавательной деятельности " .
4. Рощина Н. Л. " О воспитании эстетического вкуса учащихся при решении планиметрических задач ".
5. Ташес Е. Г. " Методика обучения отстающих учащихся " .
6. Усатова Е. В. " Соревнования на уроках математики ".
7. Финкельштейн В. М. " Заинтересовать учеников "


 Получите свидетельство
Получите свидетельство Вход
Вход



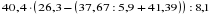 .
.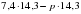 при р = 6,4. Незнайка начал решать так:
при р = 6,4. Незнайка начал решать так: 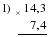
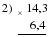
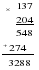
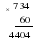
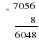
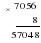
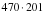
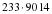
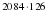




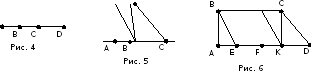
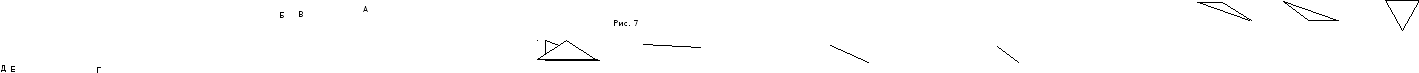
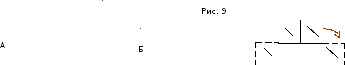












 Материал по математике по теме "Организация восприятия учебного материала школьниками с разным уровнем обученности на уроках математики" (0.14 MB)
Материал по математике по теме "Организация восприятия учебного материала школьниками с разным уровнем обученности на уроках математики" (0.14 MB)
 0
0 2709
2709 30
30 Нравится
0
Нравится
0


