ОБУЧЕНИЕ РЕШЕНИЮ ЗАДАЧ ПО ГЕОМЕТРИИ НА ОСНОВЕ “GEOGEBRA”
Христофорова А.В.
Существует несколько систем динамической геометрии, которые могут помочь школьнику при решении задач. К таким относятся GeoGebra, Kig, KSEG.
Система GeoGebra – свободно-распространяемая динамическая геометрическая среда, которая дает возможность создавать чертежи в планиметрии, в частности, для построений с помощью циркуля и линейки .
Система GeoGebra поможет учителям для объяснения, а школьникам в ознакомлении с учебными материалами не только курса геометрии, но и алгебры, математического анализа, будет незаменима для формирования навыков наглядного представления геометрических ситуаций.
У программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т. д.) за счет команд встроенного языка , который позволяет управлять и геометрическими построениями.
Программа написана Маркусом Хохенвартером на языке Java (работает на большом числе операционных систем), переведена на 39 языков и полностью поддерживает русский язык.
Систему можно использовать для построения линий:
построение графиков функций y = f (x);
построение конических сечений:
коника произвольного вида — по пяти точкам.
окружность по центру и точке на ней, по центру и радиусу, по трем точкам;
эллипс – по двум фокусам и точке на кривой;
парабола – по фокусу и директрисе;
гипербола – по двум фокусам и точке на кривой;
В системе предусмотрена возможность построения геометрического места точек, зависящих от положения некоторой другой точки, принадлежащей какой-либо кривой или многоугольнику (инструмент локус).
Кроме графических действий в системе могут быть выполнены вычисления:
действия с матрицами: сложение, умножение; транспонирование, инвертирование; вычисление определителя;
вычисления с комплексными числами;
нахождение точек пересечения кривых;
статистические функции:
вычисление математического ожидания, дисперсии;
вычисление коэффициента корреляции;
аппроксимация множества точек кривой заданного вида: полином; экспонента; логарифм; синусоида.
Задача 1. Треугольник АВС задан точками: А(9;–5), В(–7;–8), С(–5;–2). С помощью программы GeoGebra необходимо:
1) найти периметр треугольника;
2) найти уравнения сторон треугольника;
3) найти уравнение медианы АМ;
4) найти уравнение высоты BH;
5) найти уравнение прямой, проходящей через вершину A параллельно стороне ВC;
6) найти радиус описанной окружности.
Решение:
1. Чтобы найти периметр треугольника АВС, нужно выполнить следующие построения:
a) построить вершины треугольника АВС (рисунок 31). Для этого в командной строке программы с клавиатуры последовательно ввести координаты точек в формате, ввод завершается нажатием Enter:
А=(9, –5)
В=(–2, –3)
С=(5, 2)
Важно ввод осуществлять именно в таком синтаксисе, например, разделителем между координатами должна быть запятая и т. д.
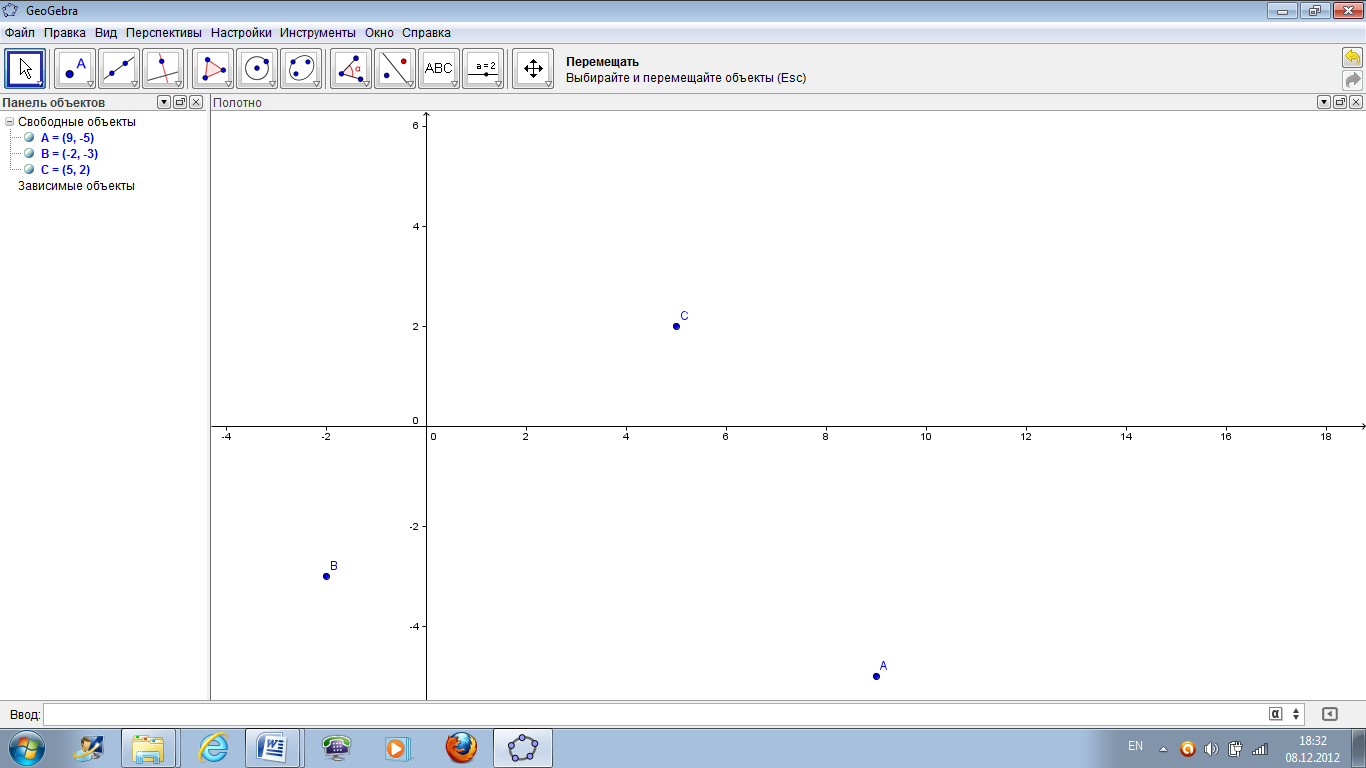
Рисунок 31 – Построение точек по координатам в программе GeoGebra.
b) построить стороны треугольника. Для этого на панели инструментов в открывающемся списке кнопки Прямые и отрезки выбрать пункт Отрезок по двум точкам (рисунок 32). Затем левой кнопкой мыши указать концы необходимых отрезков АВ, ВС, АС (рисунок 33).
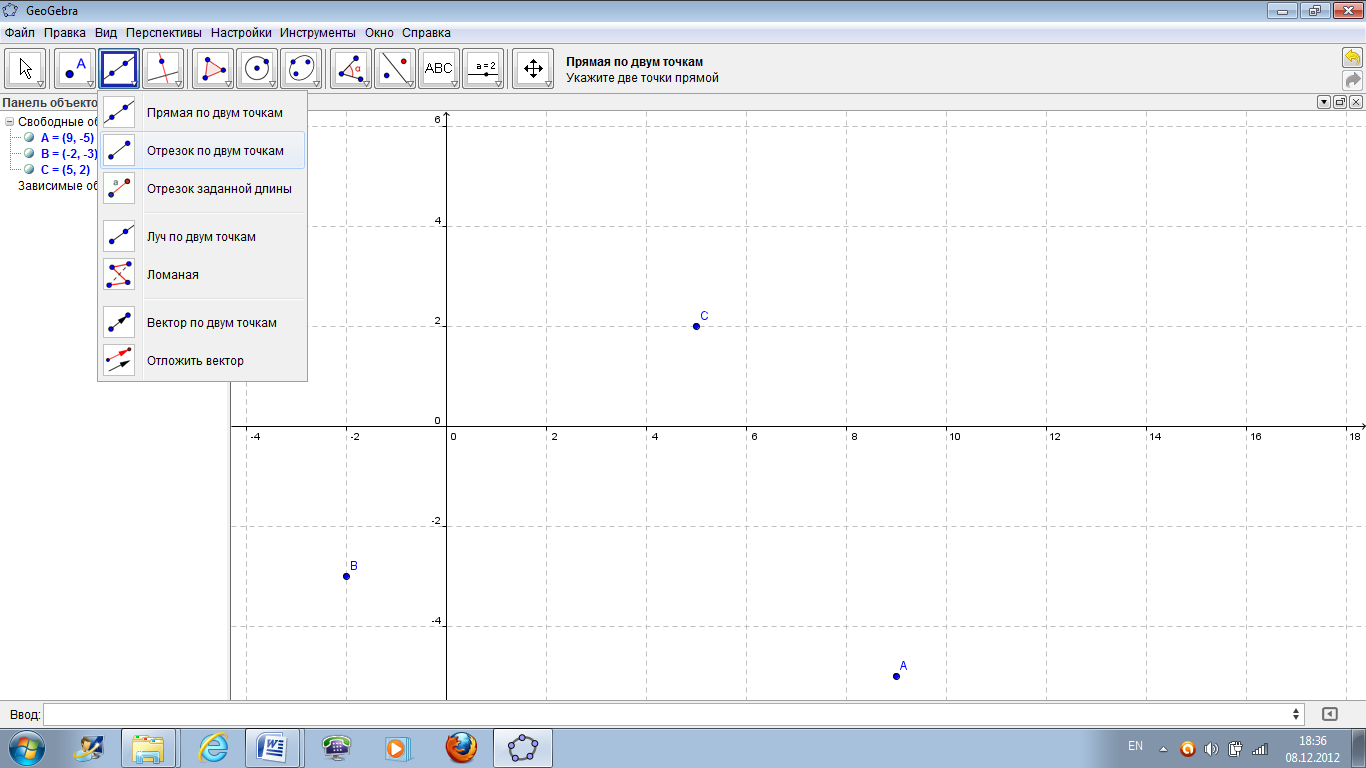
Рисунок 32 – Открывающийся список кнопки «Прямые и отрезки».
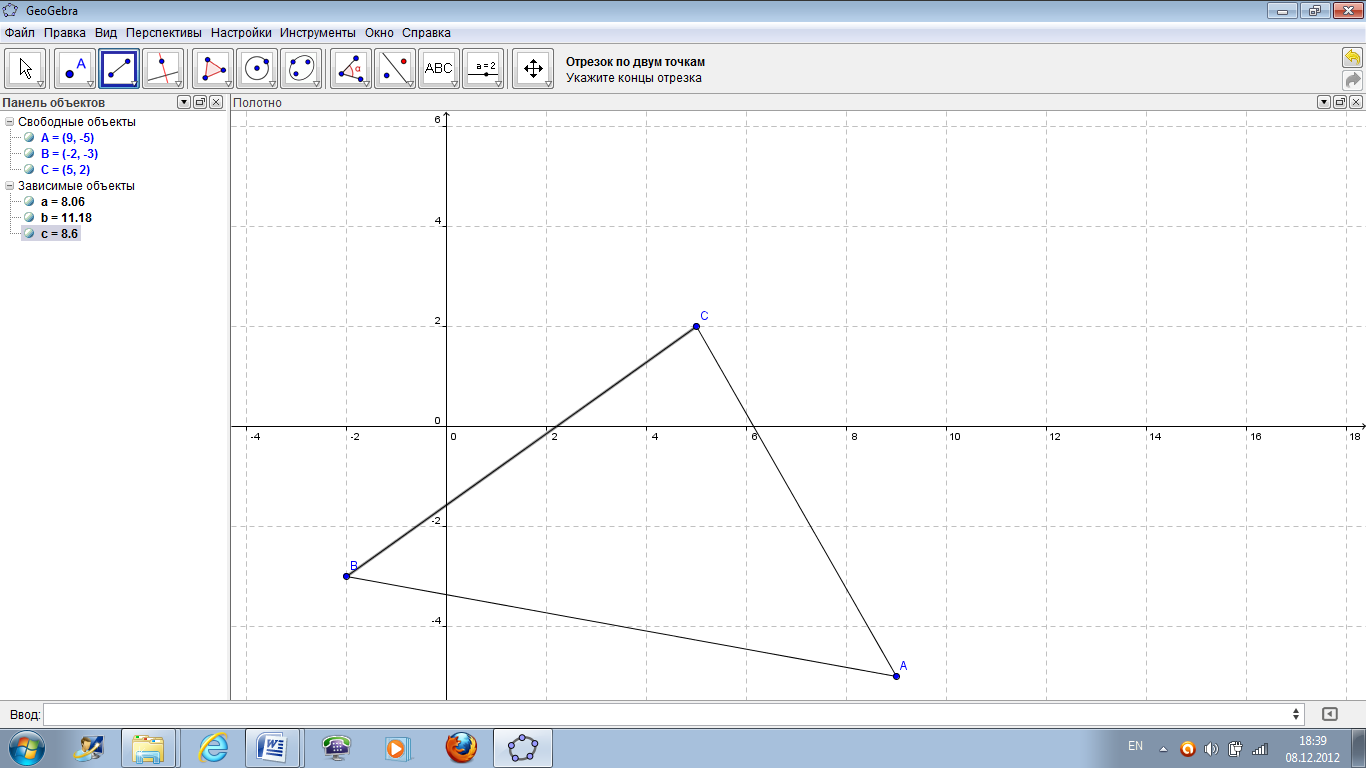
Рисунок 33 – Построение отрезков АВ, ВС, АС.
В списке свободных и зависимых объектов в окне программы слева правой кнопкой мыши по каждому объекту – отрезку АВ, ВС, АС вызвать контекстное меню (рисунок 34), в котором нужно убрать флажок отображения названия объекта и вызвать окно диалога – свойства объекта (рисунок 35), в котором указать имя объекта а (сторона треугольника, лежащая напротив угла А). Аналогично следует поступить с другими отрезками.
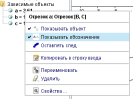
Рисунок 34 – Контекстное меню.
Рисунок 35 – Окно свойств объекта.
с) как видно на рисунке 33, в списке объектов вместе с названием сторон треугольника указаны длины его сторон. Чтобы найти периметр треугольника, нужно выполнить еще одно действие – найти сумму длин сторон, для чего в командной строке программы ввести текст «perimetr=a+b+c» и нажать Enter. После этого в списке объектов появится переменная perimeter, значение которой равно периметру треугольника (рисунок 36). В качестве разделителя целой и дробной части в десятичных дробях программа использует точку.
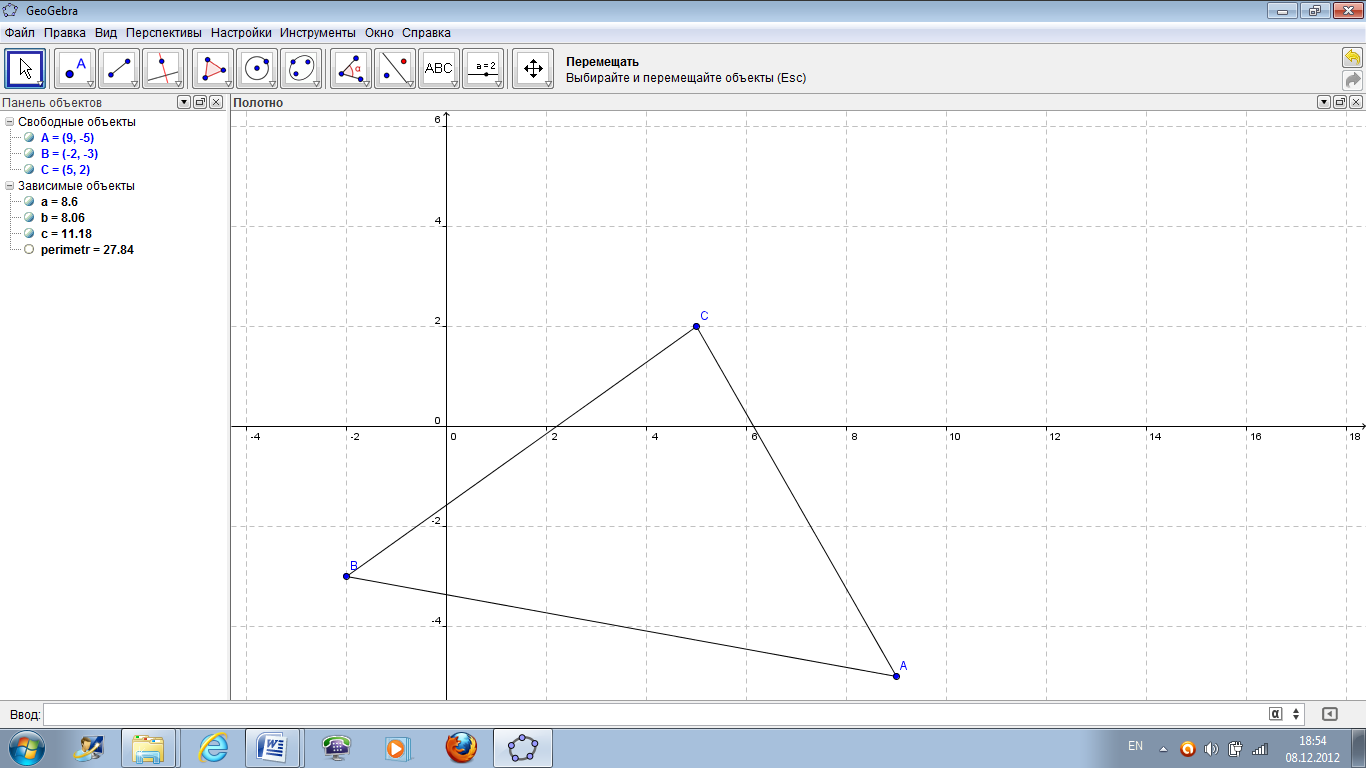
Рисунок 36 – Список объектов.
2. Чтобы найти уравнения сторон треугольника, достаточно построить прямые через вершины треугольника (содержащие стороны треугольника), и в списке объектов будет отображены общие уравнения этих прямых.
На панели инструментов в открывающемся списке кнопки Прямые и отрезки нужно выбрать пункт Прямая по двум точкам (рисунок 32). Затем левой кнопкой мыши указать необходимые точки.
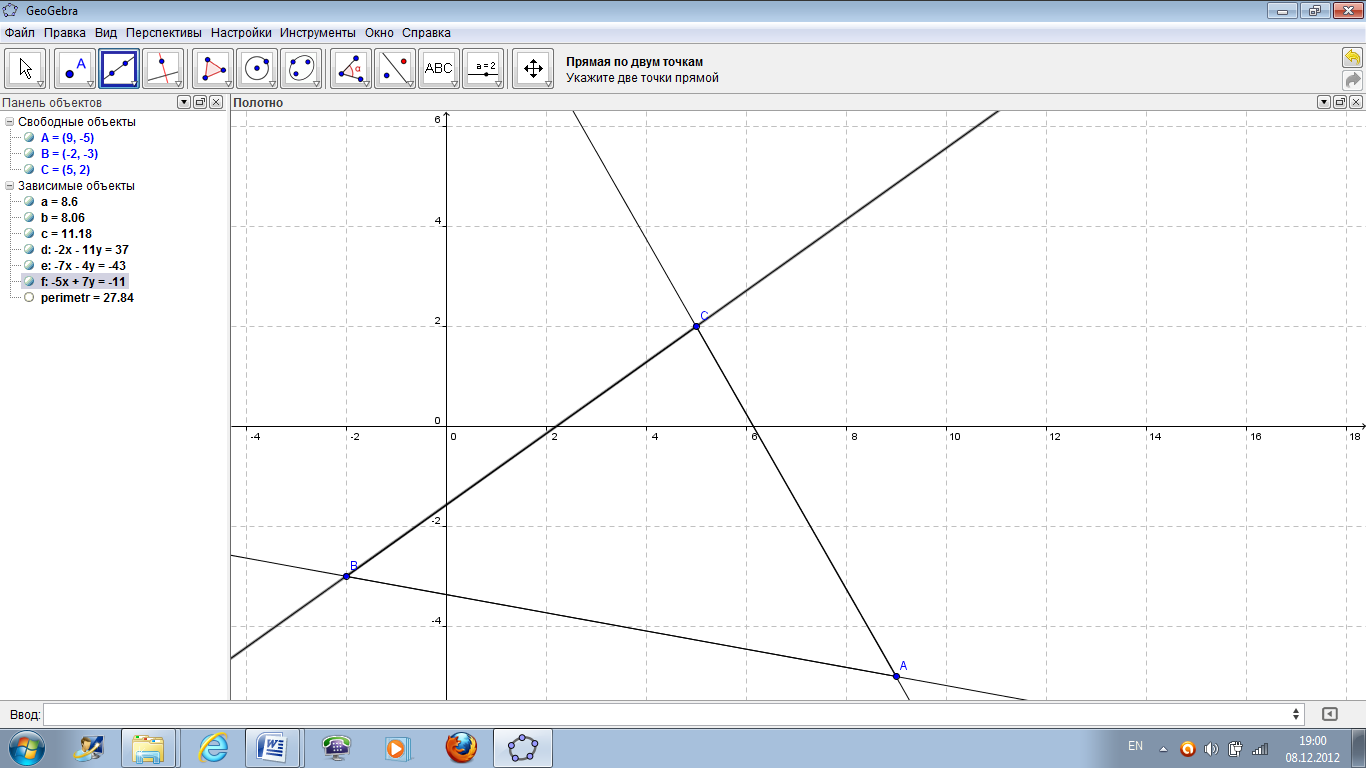
Рисунок 37 – Уравнения сторон треугольника.
Уравнения сторон треугольника:
AB: –2x – 11y = 37 (прямая d на чертеже – рисунок 37)
АС: –7х–4y = –43 (прямая e на чертеже – рисунок 37)
BC: –5x + 7y = –11 (прямая f на чертеже – рисунок 37)
3. Найти уравнение медианы АМ. С помощью инструмента Середина или центр (рисунок 38) построить середину стороны ВС – точку М. Затем построить прямую АМ, обозначить ее m, таким образом, нашли ее уравнение (рисунок 39):
Рисунок 38 – Открывающийся список кнопки «Точка».
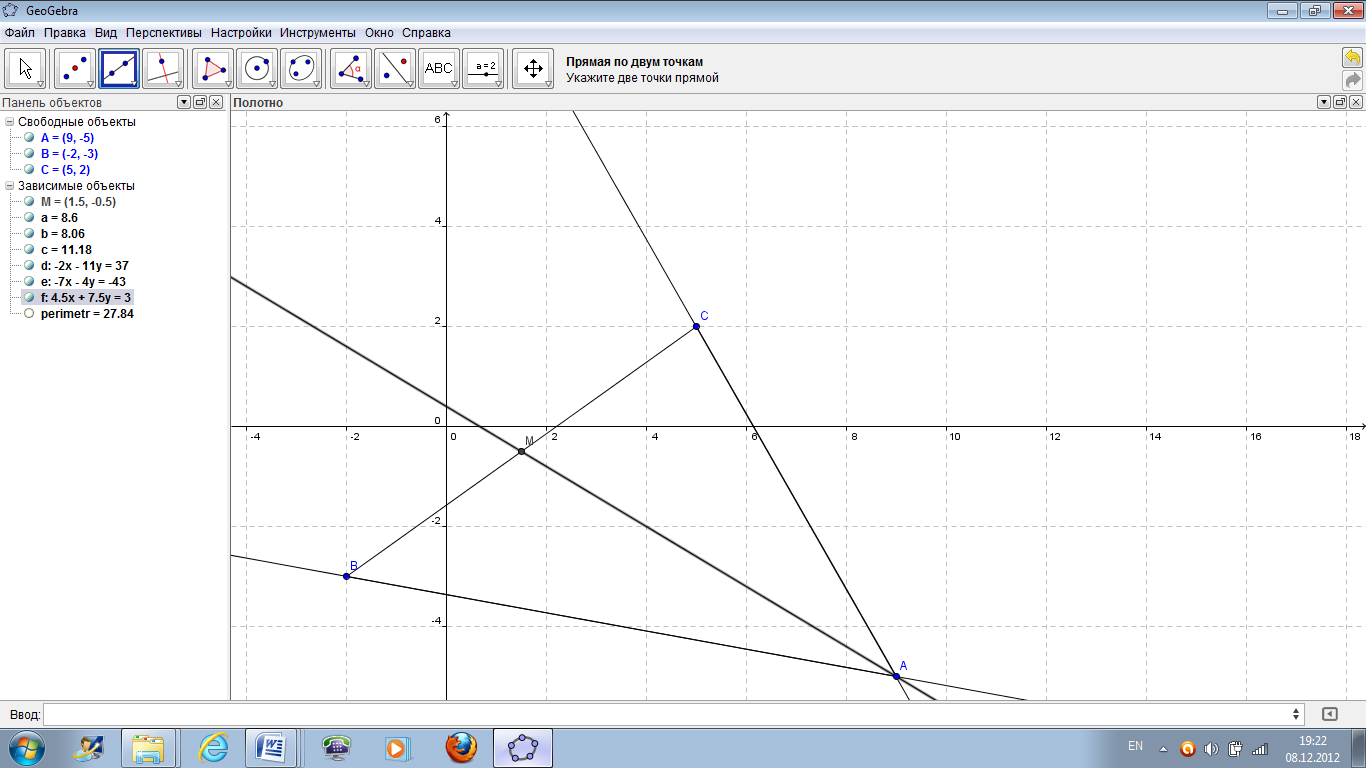
Рисунок 39 – Поиск уравнения медианы АМ.
Уравнение медианы АМ: 4.5x+7.5y=3
4. Найти уравнение высоты BH. Для начала с помощью инструмента Перпендикулярная прямая (рисунок 40) нужно построить высоту BH, обозначить ее h. В списке объектов появится ее уравнение (рисунок 41).

Рисунок 40 – Открывающийся список кнопки «Перпендикулярная
прямая».
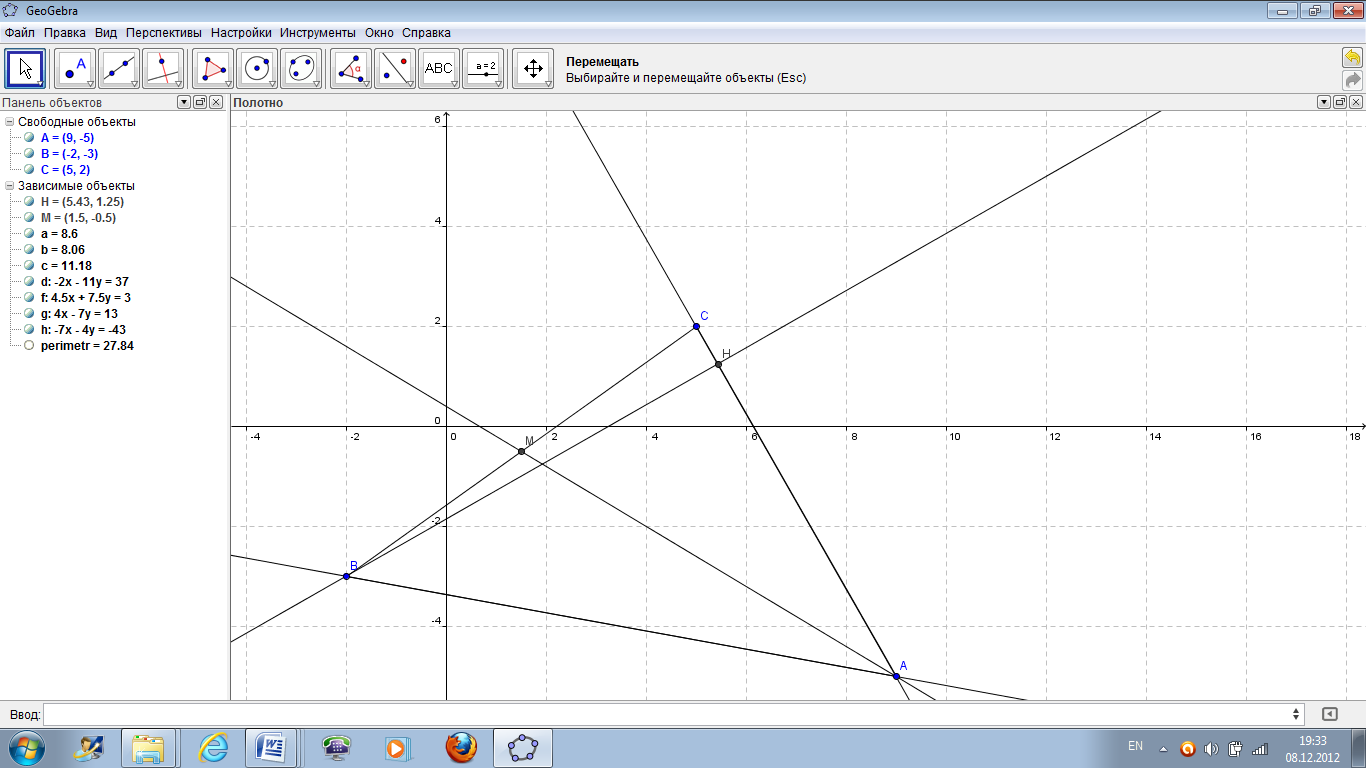
Рисунок 41 – Уравнение высоты BH.
Уравнение высоты BH: –7х–4y = –43
5. Найти уравнение прямой, проходящей через вершину С параллельно стороне АВ. С помощью инструмента Параллельная прямая (рисунок 40) построить эту прямую и обозначить ее l. В списке объектов появляется ее уравнение: l=2x+11y=32 (рисунок 42).
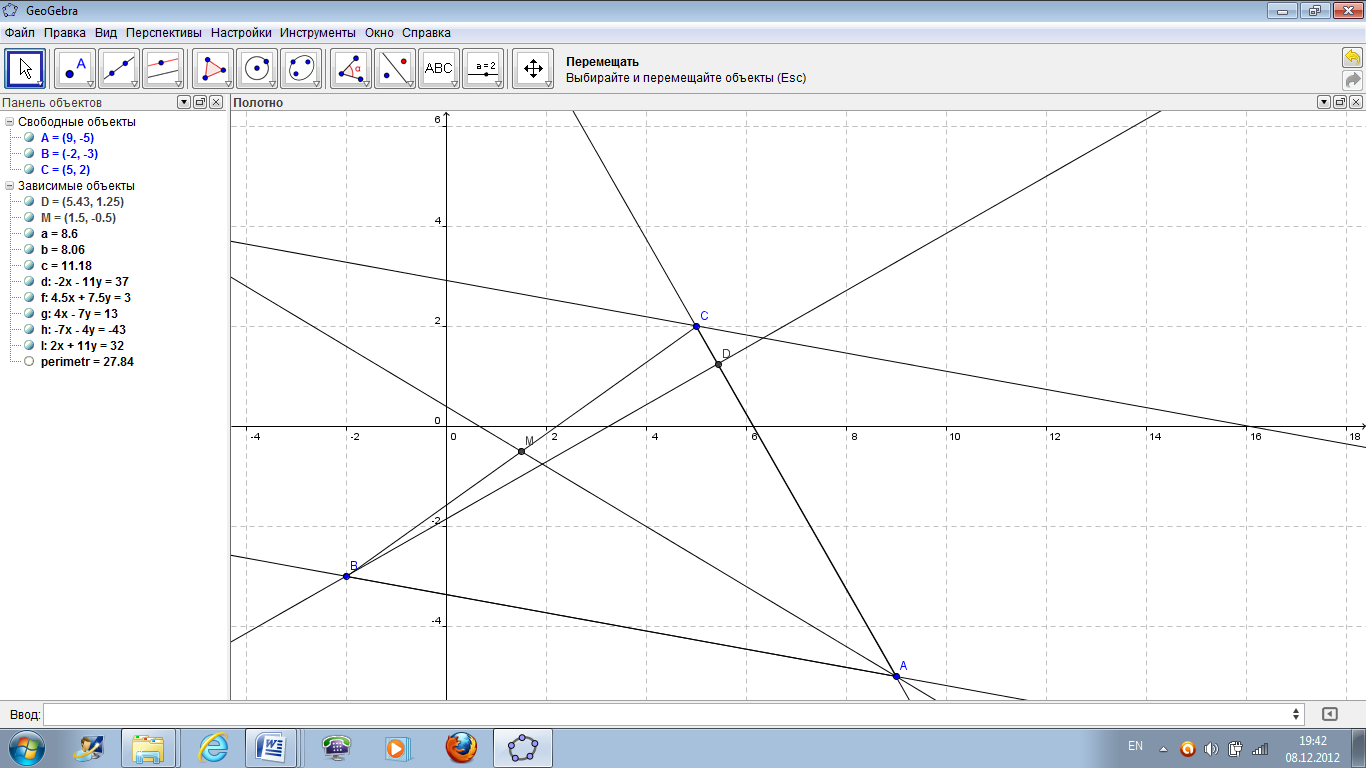
Рисунок 42 – Поиск уравнения прямой, проходящей через вершину С
параллельно стороне АВ.
6. Найти радиус описанной окружности. Самый простой способ решения – с помощью инструмента Окружность по трем точкам (рисунок 43) построить описанную окружность через точки А, В и С (рисунок 44). В списке объектов отображается уравнение построенной окружности w. Квадрат радиуса равен примерно 31.57, а сам радиус равен 5.61. Кроме этого координаты центра окружности имеют вид: (3.6; –3.44). w=(x–3.6)2 +(y+3.44)2=31.57
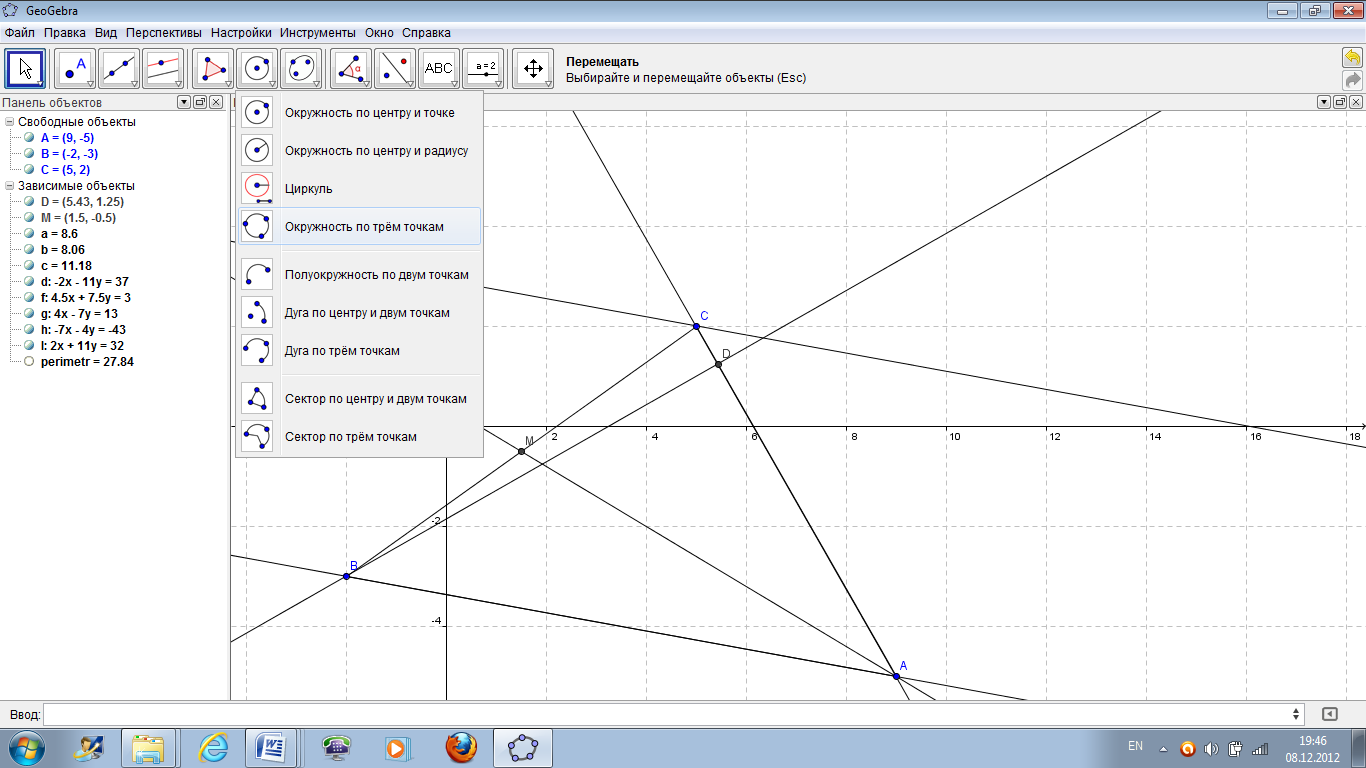
Рисунок 43 – Открывающийся список кнопки «Окружность».
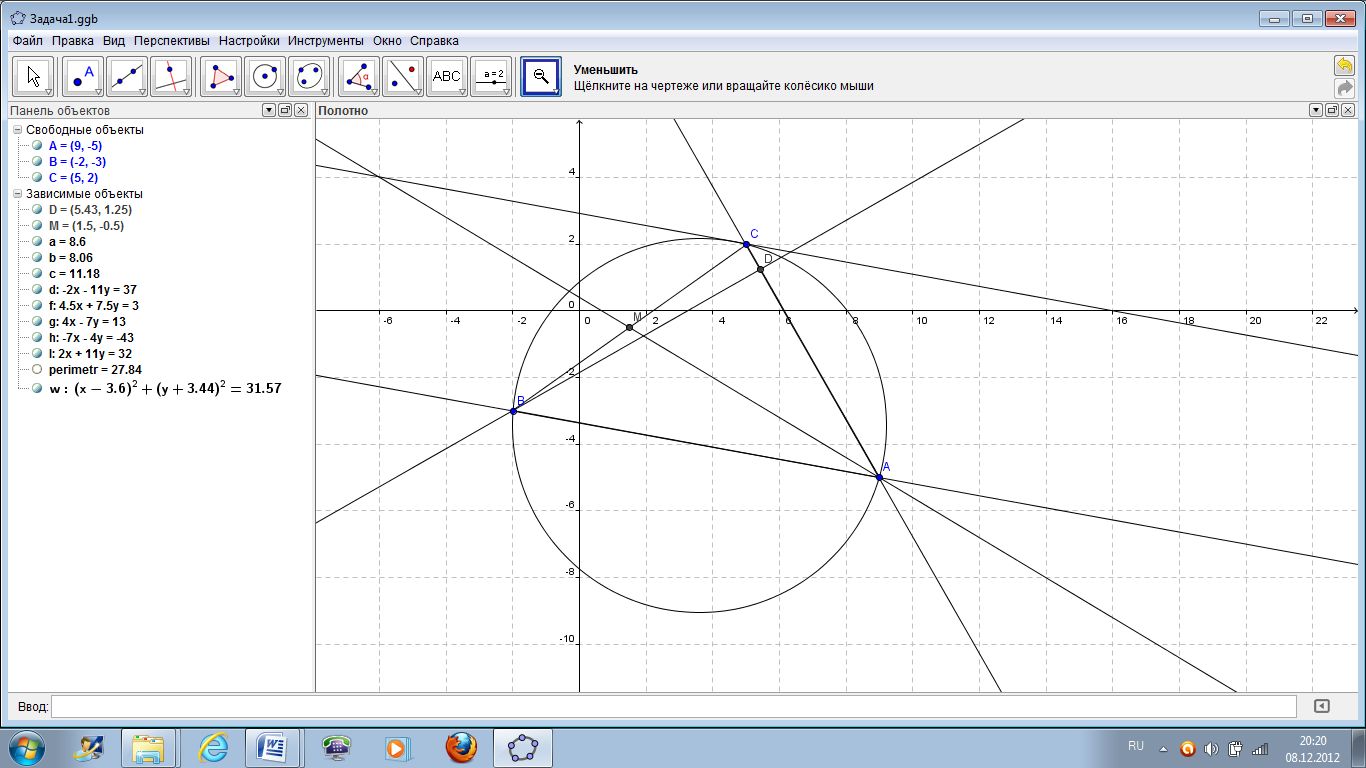
Рисунок 44 – Решение задачи 1.
Задача 2. С помощью GeoGebra построить область плоскости заданную системой линейных неравенств. Найти координаты вершин полученного многоугольника.
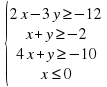
Алгоритм построения:
1) в командную строку ввести уравнения прямых – границ заданных полуплоскостей, построив тем самым прямые а, b, c;
2) определить по неравенствам заданные полуплоскости и замкнутую область – многоугольник решений;
3) построить вершины этого многоугольника A, B, C, D, как точки пересечения соответствующих прямых.
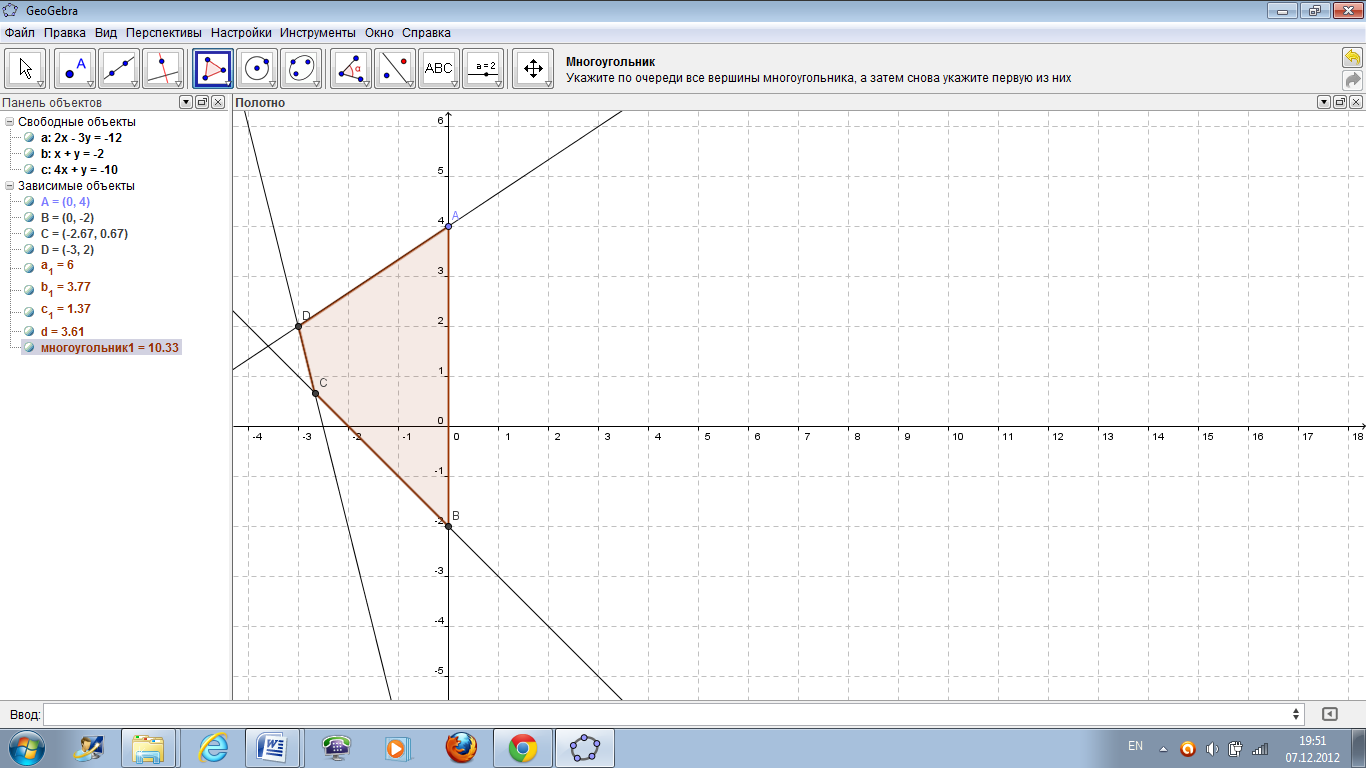
Рисунок 46 – Решение задачи 2.
В списке объектов отображены искомые координаты вершин многоугольной области и указана площадь многоугольника.
Система GeoGebra как универсальный программный продукт, сочетающий в себе свойства систем динамической геометрии, систем вычислительной математики, является полноценной компьютерной математической средой, и это дает основания для использования ее в обучении геометрии. Применение системы GeoGebra позволяет по-новому строить методику изучения геометрии, повышая наглядность, увеличивая долю эмпирической составляющей в процессе познания геометрических теорий и расширяя сферу предметных и учебных задач.


 Получите свидетельство
Получите свидетельство Вход
Вход

















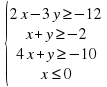










 Материал для учителей "Обучение решению задач по геометрии на основе программы "Geogebra"" (1.37 MB)
Материал для учителей "Обучение решению задач по геометрии на основе программы "Geogebra"" (1.37 MB)
 0
0 2193
2193 195
195 Нравится
0
Нравится
0


