Цель:
закрепить знания учащихся на нахождение производных тригонометрических функций.
Ключевые идеи:
Для нахождения производных тригонометрических функций используются формулы (sinx)' = cosx, (cosx)' = - sinx, (tgx)' = 1/cos2x, (ctgx)' = 1/sin2x
Результаты обучения:
учащиеся умеют решать различные примеры на нахождение производной, используя формулы производных тригонометрических функций.
Ход урока.
1. Организационный момент.
Разделить учащихся на структурированные группы.
Начать со слов Н. А. Назарбаева: «Развитие Казахстана в ХХІ веке будет напрямую связано с повышением уровня образования.
- Наша задача - поднять Казахстан на уровень международного стандарта, и наша молодежь, подрастая, будут важной элитой, которая будет вести Казахстан в большой глобальный мир.
«Только высокообразованная нация может быть конкурентоспособной», — отметил Президент РК Н. А. Назарбаев
Раздать оценочные листы. Объяснить принцип работы с ними. (3 мин)
II. Проверка домашнего задания.
Актуализация опорных знаний.
Группы получают названия по жузам.
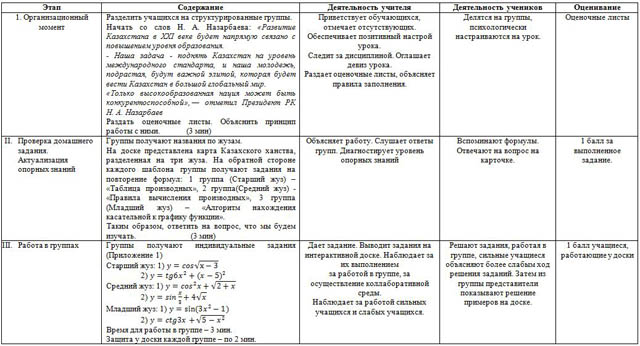
На доске представлена карта Казахского ханства, разделенная на три жуза. На обратной стороне каждого шаблона группы получают задания на повторение формул: 1 группа (Старший жуз) – «Таблица производных», 2 группа(Средний жуз) -«Правила вычисления производных», 3 группа (Младший жуз) – «Алгоритм нахождения касательной к графику функции».
Таким образом, ответить на вопрос, что мы будем изучать.(3 мин)
III. Работа в группах.
Группы получают индивидуальные задания... (Приложение 1)
Время для работы в группе – 3 мин.
Защита у доски каждой группе – по 2 мин.
«Кыз куу»
Делятся на группу девочек и группу мальчиков.
Задание: на скорость решить примеры, представленные на слайде...
IV. Физминутка «Кара жорга».
Выполнить танцевальные движения под музыку. (2 мин)
V. Групповая работа.
Состязание: Чтобы достичь независимости наша страна прошла долгий и тяжелый путь. Сейчас (слайд) ваша задача – дойти до флага нашей страны. Для этого ученикам также необходимо преодолеть путь, который состоит из заданий на нахождение производной функции.
1) f(x) = x/(sinx+1), найдите: f'(0)
2) Написать уравнение касательной к графику функции f(x) = sinx+1 в точке x0 = П/2.
3) Решить уравнение f'(x) = 0, если f(x) = cos3x - 3x.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



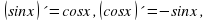

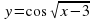
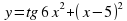



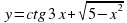
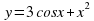
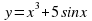
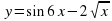
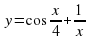
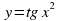




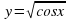
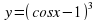
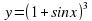
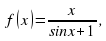 найдите:
найдите: 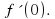
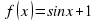 в точке
в точке 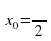 .
.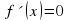 , если
, если 








 Краткосрочное планирование урока по алгебре "Производные тригонометрических функций" (36.81 КB)
Краткосрочное планирование урока по алгебре "Производные тригонометрических функций" (36.81 КB)
 0
0 1294
1294 263
263 Нравится
0
Нравится
0


