Тема занятия: «В мире закономерных случайностей»
Цели занятия:
ДИДАКТИЧЕСКАЯ ЦЕЛЬ: Выработать умение распознавать и решать основные типы вероятностных задач; показать учащимся с помощью задач, что шанс выиграть в лотереях и др. азартных играх очень мал.
Образовательные:
в системе научного познания мира.
повторить основные понятия: событие, исход, вероятность, вырабатывать умения и навыки вычислять вероятность, используя её классическое определение.
применять полученные знания, как при решении задач, так и практической деятельности; в жизненной ситуации;
Учебная задача:
В процессе занятия осуществляется формирование следующих общеучебных умений:
учебно-интеллектуальные умения:
- умение диалектически анализировать;
- умение сравнивать, обобщать, систематизировать, конкретизировать, синтезировать;
- умение формулировать проблемы, исследовательские умения (постановка задач, выработка гипотезы, выбор метода решения);
учебно-познавательные умения:
- умение участвовать в учебном диалоге;
-умение задавать уточняющие вопросы, формулировать;
-умение пользоваться математическим языком, математически грамотно выражать свои мысли;
учебно-организационные умения:
-умение организовать себя на выполнение поставленной задачи;
-умение осуществлять самоконтроль и самоанализ учебной деятельности;
-умение сотрудничать при решении учебных задач
Развивающие:
создавать условия, способствующие развитию познавательного интереса и творческой активности и формированию логического мышления, развитие математической грамотности и навыков самостоятельной работы, взаимоконтроля и самоконтроля;
способствование развитию познавательного интереса посредством создания проблемных ситуаций на занятии;
Воспитательные:
воспитание у обучающихся глубокого интереса к математике и её приложению;
выработка привычки к постоянной занятости, воспитание отзывчивости, трудолюбия, аккуратности;
воспитание культуры умственного труда;
воспитание культуры общения, культуры ведения учебного диалога (учитель-обучающийся, обучающийся-обучающийся).
воспитание чувства ответственности за результаты своего труда.
Здоровьесберегающий элемент занятия заключается в создании эмоционально благоприятных условий для всех участников образовательного процесса через доброжелательное отношение, чередующиеся формы учебной деятельности, через использование физкультпаузы.
Тип занятия:
Формы организации учебной деятельности:, диалог, частично-поисковая деятельность, индивидуальная самостоятельная, коллективная.
Методы обучения: создание проблемной ситуации, осуществление педагогической поддержки, создание ситуации взаимопомощи и взаимоконтроль.
Структура занятия:
Организационная установка, эмоциональный настрой.
Сообщения об использовании вероятностных методов в жизни.
Рассмотрение основных понятий данной науки путем последовательного выстраивания проблемных ситуаций.
Рассмотрение типичных «опытов» в данной теме.
Формирование новых знаний через решение задач.
Разбор исследовательской задачи на вероятность выигрыша в российских лотереях.
Физкультминутка.
Закрепление полученных знаний посредством самостоятельной работы с последующим контролем.
Подведение итогов и результатов занятия (рефлексия).
Продолжительность занятия 40 минут
Форма занятия: – смешанное занятие (лекция, практическая, творческая работа).
План занятия
| № | Этапы урока | Временные рамки |
| 1 | Организационная установка. Эмоциональный настрой | 1 мин. |
| 2 | Обзор обучающими по вопросу «История развития науки». Сообщения об использовании вероятностных методов в жизни. | 6 мин. |
| 3 | Рассмотрение типичных «опытов» в данной теме. Решение задач №3 ЕГЭ 2023 | 15 мин. |
| 4 | Разбор исследовательской задачи на вероятность выигрыша в российских лотереях. | 5 мин. |
| 5 | Самостоятельная работа с последующей проверкой | 10 мин. |
| 6 блок | Рефлексия. | 3 мин. |
Ход занятия
Организационная установка, эмоциональный настрой.
Философы говорят: «Путь, которым мы идем к каждой нашей цели, вымощен бесконечным множеством случайностей».(слайды 1-7)
Случай, случайность – с ними мы встречаемся повседневно: случайная поломка, случайная находка, случайное открытие, случайная ошибка, случайная встреча… Этот ряд можно продолжать бесконечно. Казалось бы, тут нет места для математики – какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности, которые позволяют нам чувствовать себя уверенно при встрече со случайными событиями.
Так, как мы продолжаем изучать раздела, то, что мы с вами должны будем сделать (обучающиеся сами пытаются поставить цели занятия)
Таким образом, целями нашего занятия будут:
Повторить основные понятия данного раздела математики.
Выяснить как они взаимосвязаны друг с другом (т.е. установить закономерности).
Научиться применять (использовать) изученный материал на практике (т.е. при решении задач) и в жизни (что является очень важным) (вероятность выигрыша в азартные игры рассматривается во второй половине занятия).
В настоящее время теория вероятностей имеет статус точной науки наравне с арифметикой, алгеброй, геометрией, тригонометрией и т.д. Этот раздел математики входит в учебники и, в КИМЫ ЕГЭ
Но начиналось всё весьма и своеобразно…
Итак, добро пожаловать в мир «математики случая и закономерных случайностей»! (слайд 7).
Первые понятия теории вероятностей возникли под влиянием азартных игр, особенно, игры в кости (слайд 8).
Математики по этому поводу шутя, говорили, что глупая игра в кости породила большую и мудрую науку, очень важную для практической деятельности людей, в то время как умная игра в шахматы в истории науки никакой роли не сыграла.
Азартные игры появились еще на заре человечества. Так, в археологических раскопках, начиная с V тысячелетия до нашей эры, можно обнаружить астрагалы – специально обработанные кости животных с нанесенными на них точками (слайд 9).
Самый древний игральный кубик найден в Северном Ираке и относится к IV тыс. до н.э.
Для кого-то кости, еще в те времена, становились источником богатства, для кого-то – причиной нищенства и позора.
Обзор обучающимися по вопросу «Для чего нам нужна теория вероятности», сообщения об использовании вероятностных методов в жизни.
А где еще используются вероятностные методы?
Сообщение 1
Вероятностно-статистические методы широко применяются в исторических исследованиях, особенно в археологии для расшифровки надписей на языке древних народов. Так, например, при расшифровке древнего иероглифического письма Ж. Шампольон учитывал вероятностные закономерности языка.
Сообщение 2
Вероятностные методы используются для установления авторства и изобличения литературных подделок. Пример из нашей недавней истории. Это споры об авторстве "Тихого Дона". Довольно многие считали, что в 23 года М.А. Шолохов не мог написать такую глубокую и поистине великую книгу. И только вероятностно-статистические методы развеяли эти сомнения. В результате чего ему была присуждена Нобелевская премия в области литературы.
Сообщение 3
Ещё один яркий пример из нашей истории. в 1968 году между командами СССР и Италии состоялся полуфинальный матч на первенство Европы, который закончился ничьей. Было дано дополнительное время и серия пенальти, но и это не выявило победителя. Тогда было решено, что победителя определит его величество случай. Бросили монету. Случай был благосклонен к итальянцам (слайд 16).
Можно без преувеличения сказать, что вероятностно-статистическими методами сегодня пронизана вся наша жизнь.
Рассмотрение основных понятий данной науки путем последовательного выстраивания проблемных ситуаций.
Рассмотрение типичных «опытов» в данной теме.
Закрепление знаний через решение задач.
Но все же, мы сказали, что теория вероятности – это наука.
Каждая наука, при изучении явлений материального мира, использует те или иные понятия, среди которых обязательно есть ОСНОВНЫЕ.
Например, в стереометрии ОСНОВНЫМИ являются понятия точка, прямая и плоскость. Какое же понятие будет основным в теории вероятности? Попробуйте догадаться.
РЕБУС: событие (СЛАЙД 17).

Верно, в теории вероятности основным является понятие события.
Повторения определений:
Событие – это результат, полученный в процессе опыта, испытания или наблюдения (слайд 18).
Пример, со слайда и обозначение заглавными буквами латинского алфавита.
Зачастую при проведении опыта будут наступать те или иные события, неизвестные заранее (так вот их мы будем называть случайными).
Определение: Случайное событие – событие, которое может произойти или не произойти при проведении данного испытания (слайд 19).
Рассмотрим несколько наиболее излюбленных в теории вероятностей примеров случайных экспериментов.
Опыт 1: Подбрасывание монеты. Испытание – подбрасывание монеты; события – монета упала гербом или решкой. ![]()
![]() (слайд 19).
(слайд 19).
Опыт 2: Подбрасывание кубика. Это следующий по популярности после монеты случайный эксперимент.

Испытание: подбрасывание кубика, события: как может упасть кубик? (1,2,3,4,5,6) и др. (слайд 20).
Опыт 3: Выбор перчаток. В коробке лежат 3 пары одинаковых перчаток. Из нее, не глядя, вынимаются две перчатки.

Испытание:
Событие: ПП, ЛЛ, на разные руки (акцент не делать на ПЛ и ЛП) (слайд 21).
Опыт 4: «Завтра днем – ясная погода». Здесь испытание: наступление дня.
События: (можно записать маркером на доске)
А – ясная погода.
В – пасмурная погода.
С – погода с переменной облачностью (слайд 22).
Опыт 5. Завтра будет вторник. (Не будет случайным событием и наступит при любых условиях) ДОСТОВЕРНЫМ (слайд 22).
Опыт 6. Следующий год будет 2024. (Не будет случайным событием и не наступит ни при каких условиях) НЕВОЗМОЖНЫМ (слайд 22).
В тетрадях делаем схему: «Типы событий» (слайд 23).
Определение: Достоверное – обязательно произойдет в результате данного испытания.
Приведите примеры.
пример:
наступление дня по прошествии ночи – достоверное событие;
при подбрасывании кубика выпадет одна из цифр 1,2,3,4,5 или 6. как вы думаете, предсказанное событие наступит или нет? конечно, обязательно наступит.
1. после зимы наступает весна.
2. после ночи приходит утро.
3. камень падает вниз.
4. вода становится теплее при нагревании.
Определение: Невозможное – не может произойти в результате данного испытания.
Примеры:
– при подбрасывании кубика выпадет цифра 7. как вы думаете, предсказанное событие наступит или нет? конечно, нет.
з0 февраля день рождения.
при подбрасывании кубика выпадает 7 очков.
человек рождается старым и становится с каждым днем моложе.
«это невероятно…»
«это маловероятно, что…»
«более вероятно, что…»
«можно утверждать со стопроцентной вероятностью, что…» (слайд 30).
Когда мы используем подобные фразы?
Подобные фразы мы используем тогда, когда пытаемся спрогнозировать наступление того или иного события. При этом мы опираемся на интуицию, жизненный опыт, здравый смысл и т.д.
Например, мы заранее знаем, что в кинотеатр на детский сеанс пойдет большинство школьников, чем взрослых и ненужно ничего здесь высчитывать.
Однако в жизни чаще встречаются события, сравнить и оценить которые, основываясь только на интуиции, невозможно и трудно.
Например, банки с бракованной краской. Какой шанс у вас купить эту банку или не купить?
Т.е. нам будет нужна точная количественная оценка наступления случайного события. Такую оценку и называют вероятностью события (слайд 31).
Итак, пусть N – число всевозможных исходов данного испытания;
N(A) – число благоприятных исходов (т.е. тех исходов, в которых наступает событие А).
Определение: Вероятностью наступления события А при проведении испытания называется отношение числа благоприятных исходов, к числу всевозможных исходов этого испытания.
Т.е. 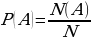
Задача в таблице (слайд 32). Испытание : подбрасывание игрального кубика.
Задача (слайд 33). Из 25 экзаменационных билетов по технологии студент успел подготовить 11 первых и 8 последних билетов. Какова вероятность того, что на экзамене ему достанется билет, который он а) подготовил; б) не подготовил.
Задача (слайд 34). Найти вероятность события: «Случайным образом выбранное двузначное число делится на 15».
Задача (слайд 35). Из карточек составили слово «статистика». Какую карточку с буквой вероятнее всего вытащить?
Задача (слайд 36). Для новогодней лотереи отпечатали 200 билетов из них 20 выигрышных. Какова вероятность того, что купленный билет окажется выигрышным.
Разбор исследовательской задачи на вероятность выигрыша в российских лотереях.
А сейчас мы с вами посмотрим, каковы же реальные шансы выиграть в лотерею спортлото.
Один ученик заранее работал над исследовательской задачей, связанной с азартными играми
Задача (слайд 37). Карточка «Спортлото» содержит 49 чисел. В итоге тиража выигрывают какие- то 6 чисел. Какова ( в % ) вероятность того, что на карточке вы верно угадали:
а) хотя бы одно число; (33%);
б) не более одного числа; (42%);
в) не менее трех чисел; ( 15%);
г) 4; 5 или 6 чисел; (0,12%).
Таким образом, в азартные игры играть не стоит, т.к. Шанс выиграть очень мал.
Физкультпауза.
Закрепление полученных знаний посредством самостоятельной работы с последующим контролем.
Самостоятельная работа с последующей проверкой (слайд 39).
| № | Испытание | N | Событие А | N(A) | P(A) |
| 1 | Бросание монеты |
| Выпал «орёл» |
|
|
| 2 | Подбрасывание игрального кубика |
| Выпавшее число очков кратно двум |
|
|
| 3 | Вытягивание экзаменационного билета |
| Вытянули билет № 5 |
|
|
| 4 | Случайный выбор двузначного числа |
| Число состоит из одинаковых цифр |
|
|
| 5 | Игра в лотерею (1500 билетов, из которых 120 выигрышных) |
| Выиграли, купив один билет |
|
|
| 6 | Наступление дня рождения |
| День рождения моего друга – число, меньшее 32 |
|
|
| 7 | Получение диплома |
| 10 января 2012 года вы получите диплом |
|
|
Подведение итогов и результатов занятия (рефлексия).
Ребята, ответьте на вопросы: что вы узнали нового на нашем занятии? Чему научились? Что показалось особенно трудным?
Закончить наше занятие я хочу словами великого педагога (слайд 40). Ян Амос Каменский сказал: «Считай несчастным тот день или тот час, в котором, ты не усвоил ничего, ничего не прибавил к своему образованию».
И я надеюсь, что сегодняшнее занятие, и день не будет для вас несчастным и потерянным, т.к. каждый из вас унесёт с собой, что-то новое, неизвестное, интересное, познавательное.
Самоанализ открытого занятия по математике в 10 классе
«В мире закономерных случайностей»
.
ДИДАКТИЧЕСКАЯ ЦЕЛЬ: Выработать умение распознавать и решать основные типы вероятностных задач; показать учащимся с помощью задач, что шанс выиграть в лотереях и др. азартных играх очень мал.
Образовательные:
в системе научного познания мира.
повторить основные понятия: событие, исход, вероятность, вырабатывать умения и навыки вычислять вероятность, используя её классическое определение.
применять полученные знания, как при решении задач, так и практической деятельности; в жизненной ситуации;
Учебная задача:
В процессе занятия осуществляется формирование следующих общеучебных умений:
учебно-интеллектуальные умения:
- умение диалектически анализировать;
- умение сравнивать, обобщать, систематизировать, конкретизировать, синтезировать;
- умение формулировать проблемы, исследовательские умения (постановка задач, выработка гипотезы, выбор метода решения);
учебно-познавательные умения:
- умение участвовать в учебном диалоге;
-умение задавать уточняющие вопросы, формулировать;
-умение пользоваться математическим языком, математически грамотно выражать свои мысли;
учебно-организационные умения:
-умение организовать себя на выполнение поставленной задачи;
-умение осуществлять самоконтроль и самоанализ учебной деятельности;
-умение сотрудничать при решении учебных задач
Развивающие:
создавать условия, способствующие развитию познавательного интереса и творческой активности и формированию логического мышления, развитие математической грамотности и навыков самостоятельной работы, взаимоконтроля и самоконтроля;
способствование развитию познавательного интереса посредством создания проблемных ситуаций на занятии;
Воспитательные:
воспитание у обучающихся глубокого интереса к математике и её приложению;
выработка привычки к постоянной занятости, воспитание отзывчивости, трудолюбия, аккуратности;
воспитание культуры умственного труда;
воспитание культуры общения, культуры ведения учебного диалога (учитель-обучающийся, обучающийся-обучающийся).
воспитание чувства ответственности за результаты своего труда.
Здоровьесберегающий элемент занятия заключался в создании эмоционально благоприятных условий для всех участников образовательного процесса через доброжелательное отношение, чередующиеся формы учебной деятельности, через использование физкультпаузы.
Планируемы результаты:
Учащиеся смогут решать задачи №3 из КИМов ЕГЭ по теории вероятности
Оборудование к занятию: доска, компьютер с проектором, презентация по теме данной теме, игральные кубики, монеты, урна с шарами различных цветов.
Тип занятия:
Формы организации учебной деятельности:, диалог, частично-поисковая деятельность, индивидуальная самостоятельная, коллективная.
Методы обучения: создание проблемной ситуации, осуществление педагогической поддержки, создание ситуации взаимопомощи и взаимоконтроль.
Структура занятия:
Организационная установка, эмоциональный настрой.
Сообщения об использовании вероятностных методов в жизни.
Рассмотрение основных понятий данной науки путем последовательного выстраивания проблемных ситуаций.
Рассмотрение типичных «опытов» в данной теме.
Формирование новых знаний через решение задач.
Разбор исследовательской задачи на вероятность выигрыша в российских лотереях.
Физкультминутка.
Закрепление полученных знаний посредством самостоятельной работы с последующим контролем.
Подведение итогов и результатов занятия (рефлексия).
Продолжительность занятия 40 минут
Форма занятия: – смешанное занятие (лекция, практическая, творческая работа).
Мною предусматривалась подача материала с элементами занимательности, историческими справками. Рационально распределено время на всех этапах занятия. Темп занятия соответствовал уровню развития и подготовленности учащихся.
Мною задумывался диалог между учителем и учащимися, так как класс достаточно сильный и знаком мне. Я осуществляла обратную связь, речь была достаточно грамотной, не содержала неизвестных терминов. Темп занятия был достаточно быстрым. Взаимоотношения учителя и учащихся на протяжении всего занятия носили характер сотрудничества. Ученики внимательно слушали, активно отвечали на вопросы
Занятие способствовало формированию математической грамотности учащихся, основных мировоззренческих идей, вероятностно-статистического мышления, умению различать различные события и решению вероятностных задач.
Содержание занятия способствовало развитию интереса к учению, о чем свидетельствует рефлексивный этап.
Занятие было построено методически грамотно: наличие четкой структуры, реализация каждого этапа соответствующими методами, учет дидактических принципов и целей математического образования.
Материал на занятии излагался доступным и грамотным языком.
Содержание занятия способствовало развитию интереса к учению, о чем свидетельствует рефлексивный этап.
На мой взгляд, поставленные задачи и цели занятия были достигнуты. Во время занятия удалось выполнить весь запланированный объем работы.

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект занятия по теории вероятности "В мире закономерных случайностей" (91.61 KB)
Конспект занятия по теории вероятности "В мире закономерных случайностей" (91.61 KB)
 0
0 310
310 5
5 Нравится
0
Нравится
0


