Конспект урока «Умножение и деление десятичных дробей»

Урок по теме:

«Умножение и деление десятичных дробей»

Конспект урока

Характеристика урока

Учебник: Математика. 5 класс: учеб. для учащихся общеобразоват. учреждений/Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. – 31-е изд., стер. – М.: Мнемозина, 2013. – 280с. Глава 2. Дробные числа. Параграф 7. Пункты 36, 37.

Тема: Умножение и деление десятичных дробей.

Тип урока: Урок решения задач.

Учебная задача урока: рассмотрение видов задач, решаемых на основе умножения и деления десятичных дробей.

Диагностируемые цели урока:

в результате урока ученик знает:

- алгоритм умножения десятичных дробей

- Алгоритм деления десятичных дробей

- виды задач на указанные правила

умеет:

-применять алгоритмы умножения и деления десятичных дробей для решения задач различных видов.

понимает:

- что действия умножения и деления - взаимно обратные.

Учебные действия, формируемые на уроке:

Личностные: умение учащегося устанавливать связи между целью учебной деятельности и её мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом должна осуществляться осмысленная организация собственной деятельности ученика.

Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что ещё неизвестно, планирование - определение последовательности промежуточных целей с учётом конечного результата, оценка - выделение и осознание учащимся того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения.

Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т. е. определение цели сотрудничества, функций участников, способов взаимодействия, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и  условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение.

Познавательные: анализ объектов  с целью выделения признаков (существенных, несущественных); выдвижение гипотез и их обоснование; построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей.

Методы обучения: репродуктивный, частично-поисковые, УДЕ.

Форма работы: фронтальная, групповая.

Средства обучения: традиционные, презентация.

Структура урока:

1. Мотивационно-ориентировочная часть (5 минут)

2. Операционно-познавательная часть (38 минут)

3. Рефлексивно-оценочная часть (2 минуты)

Ход урока

Мотивационно-ориентировочная часть

Актуализация

Работа идет устно. Правильные ответы выводятся на презентации.

Учитель: Выберите из предложенных чисел десятичные дроби.

1) 2134; 4) 347

2) 2 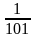; 5) 7,9

3) 0,095; 6)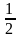

Ответ. 3, 5

Учитель: Какие числа называются десятичными дробями?

(Числа, знаменатель дробной части которых выражается единицей с одним или несколькими нулями)

Задание 1. Вычислите:

а) 2,5 0,08;

б) 0,001 1,2;

в) 12,5 : 25;

г) 4,08 : 0,4.

Ответы:

а) 2,5 0,08 = 0,2

б) 0,001 1,2 = 0,0012

Учитель: Сформулируйте алгоритм умножения десятичных дробей.

(Чтобы перемножить две десятичные дроби, надо:

1. выполнить умножение, не обращая внимания на запятые;

2. отделить запятой у получившегося результата умножения столько цифр справа, сколько их стоит после запятой в обоих множителях вместе.)

3. в) 12,5 : 25 = 0,5

4. г) 4,08 : 0,4 = 10,2

Учитель: Сформулируйте алгоритм деления на десятичную дробь.

(Чтобы разделить число на десятичную дробь, надо:

1. в делимом и делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе;

2. после этого выполнить деление на натуральное число.)

Мотивация

На предыдущих уроках вы изучали правила умножения и деления на десятичную дробь.

Постановка учебной задачи

Поэтому сегодня на уроке мы должны рассмотреть как эти правила применяются при решении задач.

Операционно-познавательная часть

Работа идёт фронтально со всем классом. По одному ученику вызывается к доске.

Задание 1. Вычислите:

а) 0,17 6,9;

б) 1,245 2,11;

в) 3,51 : 2,7;

г) 16,51 : 1,27;

д) 46,08 : 0,384 1,3;

е) 2,51 3,62 : 0,2.

Решение:

а) 0,17 6,9 = 1,173

0,17

* 6,9

153

+102

1,173

б) 1,245 2,11 = 2,62695

1,245

* 2,11

1245

+1245

2490

2,62695

в) 3,51 : 2,7 = 1,3

- 35,1 27

27 1,3

- 81

81

0

г) 16,51 : 1,27 = 13

- 1651 127

127 13

-381

381

0

д) 46,08 : 0,384 1,3 = 156

1) 46,08 : 0,384 = 120

- 46080 384

384 120

-768

768

0

2) 120 1,3 = 156

120

* 1,3

360

+120

156,0

е) 2,51 3,62 : 0,2 = 45,431

1) 2,51 3,62 = 9,0862

2,51

* 3,62

502

+1506

753

9,0862

2) 9,0862 : 0,2 = 45,431

- 90,862 2

90 45,431

- 8

8

-6

6

-2

2

0

Задача 1. Мотоциклист ехал 3,5 часа со скоростью 65,4 км/ч. Какой путь проехал мотоциклист?

Решение.

3,5 65,4 = 228,9 (км)

65,4

* 3,5

3270

+ 1962

228,90

Ответ. 228,9 км

Задача 2. Алексей проехал на поезде 162,5 км за 2,6 ч. С какой скоростью шел поезд?

Решение.

162,5 : 2,6 = 62,5 (км/ч)

- 1625 26

156 62,5

-65

52

-130

130

0

Ответ. 62,5 км/ч.

Задача 3. Алюминиевый шар, объем которого 50 см³, имеет массу 135 граммов. Чему равна масса стального шара того же объема, если масса 1 см³ алюминия на 5,2 г меньше массы 1 см³ стали?

Решение.

1. 135 : 50 + 5,2 = 2,7 + 5,2 = 7,9 (г) – масса 1 см³ стали

- 135 50

100 2,7

-350

350

0

1. 7,9 50 = 395 (г) – масса стального шара объемом 50 см³

7,9

* 50

00

+ 395

395,0

Ответ. 395 г

Задача 4. Питательный раствор для подкормки растений поступает в теплицу по двум трубам. Первая была открыта 0,6 ч, а вторая 0,4 ч. В результате поступило 3,32 л раствора. Сколько питательного раствора подается за 1 ч во второй трубе, если по первой поступает 3, 6 л раствора за 1 ч.

Решение.

1. 3,6 0,6 = 2,16 (л) поступило раствора через первую трубу за 0,6 ч

3,6

* 0,6

2,16

1. 3,32 – 2,16 = 1,16 (л) – поступило через вторую трубу за 0,4 ч

2. 1,16 : 0,4 = 2,9 (л) – поступает за 1 ч через вторую трубу

- 11,6 4

8 2,9

- 36

36

0

Ответ. 2,9 л

Задание 2. Найдите значение наиболее рациональным способом:

а) 3,5 56,47 4

б) 3,6 896,7

Решение.

а) 3,5 56,47 4 = 3,5 4 56,47 = 789,78

1) 3,5 4 = 14

3,5

* 4

14,0

2) 14 56,47 = 789,78

56,47

* 14

22508

+ 5647

789,78

б) 3,6 896,7 = 3,6 896,7 = 3586,8

1) 3,6 = 36 : 9 = 4

2) 4 896,7 = 3586,8

896,7

* 4

3586,8

Работа по группам

Карточка для I группы:

Задание 1. Найдите значение произведения.

а) 2,5 1,035 4; б) 7,5 79,6 0,4

Ответы:

а) 2,5 1,035 4 = 2,5 4 1,035 = 10,35

1) 2,5 4 = 10

2,5

* 4

10,0

2) 10 1,035 = 10,35

1,035

* 10

0000

+ 1035

10,350

б) 7,5 79,6 0,4 = 7,5 0,4 79,6 = 238,8

1) 7,5 0,4 = 3

7,5

* 0,4

3,00

2) 3 79,6 = 238,8

79,6

* 3

238,8

Задание 2. Найдите значение частного.

а) 0,8 : 0,5; б) 0,126 : 0,9;

Ответы:

а) 0,8 : 0,5 = 1,6

- 8 5

5 1,6

- 30

30

0

б) 0,126 : 0,9 = 0,14

-1,26 9

9 0,14

- 36

36

0

Задание 3. Найдите значение выражения.

а) 10,5 : 3,5 1,2; б) 0,824 : 0,8 0,3;

Ответы:

а) 10,5 : 3,5 1,2 = 3,6

1) 10,5 : 3,5 = 3

- 105 35

105 3

0

2) 3 1,2 = 3,6

1,2

* 3

3,6

б) 0,824 : 0,8 0,3 = 0,309

1) 0,824 : 0,8 = 1,03

- 8,24 8

8 1,03

- 24

24

0

2) 1,03 0,3 = 0,309

1,03

* 0,3

0,309

Задача 1.

Найдите сумму площадей стен комнаты, длина которой 6,4 м, ширина 3,5 м и высота 2,69 м. Найдите объем комнаты. Ответы округлите до десятых.

Решение.

1. 3,5+6,4 = 9,9 (м) – сумма длины и ширины комнаты

2. 19,8 2,69 = 53,262 = 53,3 (м²) – сумма площадей стен комнаты

19,8

* 2,69

1782

+1188

396

53,262

1. 6,4 3,5 2,69 =60,256 =60,3 (м³) – объем комнаты

6,4

* 3,5

320

+ 192

22,40

22,4

* 2,69

2016

+ 1344

448

60,256

Ответ. сумма площадей стен комнаты 53,3 м², объем комнаты 60,3 м³.

Задача 2. Веревку разрезали на две части. Длина одной части 3,25 м, а длина другой части в 1,3 раза меньше первой. Какова была длина веревки?

Решение.

1. 3,25 : 1,3 = 2,5 (м)

-32,5 13

26 2,5

-65

65

0

1. 2,5 + 3,25 = 5,75 (м)

Ответ. 5,75 м

Задача 3. На приготовление уроков Боря затратил в 2,5 раза меньше времени, чем на прогулку. Но на поход с родителями в магазин, он затратил в 1,5 раза больше времени, чем на прогулку. Сколько времени ушло у Бори на прогулку, поход в магазин и приготовление уроков, если прогулка заняла 2,8 ч?

Решение.

1. 2,8 : 2,5 = 1,12 (ч) – заняло приготовление уроков

- 28 25

25 1,12

- 30

25

- 50

50

0

1. 2,8 1,5 = 4,2 (ч) – занял поход в магазин

2,8

* 1,5

140

+ 28

4,20

1. 1,12 + 4,2 + 2,8 = 8,12 (ч)

Ответ. 8,12 ч

Карточка для II группы:

Задание 1. Найдите значение произведения.

а) 4,5 1,055 4; б) 8,5 76,8 0,6

Ответы:

а) 4,5 1,055 4 = 4,5 4 1,055 = 18,99

1) 4,5 4 = 18

4,5

* 4

18,0

2) 18 1,055 = 18,99

1,055

* 18

8440

+ 1055

18,990

б) 8,5 76,8 0,6 = 8,5 0,6 76,8 = 238,8

1) 8,5 0,6 = 5,1

8,5

* 0,6

5,10

2) 5,1 79,6 = 405,96

79,6

* 5,1

+796

3980

405,96

Задание 2. Найдите значение частного.

а) 0,6 : 0,5; б) 0,126 : 0,3;

Ответы:

а) 0,6 : 0,5 = 1,2

- 6 5

5 1,2

- 10

10

0

б) 0,126 : 0,3 = 0,42

-1,26 3

12 0,42

- 6

6

0

Задание 3. Найдите значение выражения.

а) 17,5 : 3,5 1,2; б) 0,824 : 0,8 0,3;

Ответы:

а) 17,5 : 3,5 1,2 = 6

1) 17,5 : 3,5 = 5

- 175 35

175 5

0

2) 5 1,2 = 6

1,2

* 5

6,0

б) 0,824 : 0,4 0,6 = 1,236

1) 0,824 : 0,4 = 2,06

- 8,24 4

8 2,06

- 24

24

0

2) 2,06 0,6 = 1,236

2,06

* 0,6

1,236

Задача 1.

Найдите сумму площадей стен офисного помещения, длина которого 7,2 м, ширина 4,5 м и высота 3,41 м. Найдите объем офисного помещения. Ответы округлите до десятых.

Решение.

1. 4,5+7,2 = 11,7 (м) – сумма длины и ширины офиса

2. 23,4 3,41 = 79,794 = 79,8 (м²) – сумма площадей стен офиса

23,4

* 3,41

234

+ 936

702

79,794

1. 7,2 4,5 3,41 =60,256 =110,484 = 110,5 (м³) – объем офиса

7,2

* 4,5

360

+ 288

32,40

32,4

* 3,41

324

+ 1296

972

110,484

Ответ. сумма площадей стен комнаты 79,8 м², объем комнаты 110,5 м³.

Задача 2. Веревку разрезали на две части. Длина одной части 5,25 м, а длина другой части в 1,2 раза меньше первой. Какова была длина веревки?

Решение.

1. 5,25 : 1,2 = 4,375 (м)

-52,5 12

48 4,375

-45

36

- 90

84

-60

60

0

1. 4,375 + 5,25 = 9,625 (м)

Ответ. 9,625 м

Задача 3. На приготовление уроков Ваня затратил в 1,5 раза меньше времени, чем на прогулку. Но на поход с родителями в магазин, он затратил в 1,8 раза больше времени, чем на прогулку. Сколько времени ушло у Вани на прогулку, поход в магазин и приготовление уроков, если прогулка заняла 1,8 ч?

Решение.

1. 1,8 : 1,5 = 1,2 (ч) – заняло приготовление уроков

- 18 15

15 1,2

- 30

30

0

1. 1,8 1,8 = 3,24 (ч) – занял поход в магазин

1,8

* 1,8

144

+ 18

3,24

1. 1,2 + 3,24 + 1,8 = 6,24 (ч)

Ответ. 6,24 ч

Карточка для III группы:

Задание 1. Найдите значение произведения.

а) 5,5 1,055 4; б) 2,5 76,8 0,6

Ответы:

а) 5,5 1,055 4 = 5,5 4 1,055 = 23,21

1) 5,5 4 = 22

5,5

* 4

22,0

2) 22 1,055 = 23,21

1,055

* 22

2110

+ 2110

23,210

б) 2,5 76,8 0,6 = 2,5 0,6 76,8 = 119,4

1) 2,5 0,6 = 1,5

2,5

* 0,6

1,50

2) 1,5 79,6 = 119,4

79,6

* 1,5

+3980

796

119,40

Задание 2. Найдите значение частного.

а) 0,4 : 0,5; б) 0,126 : 0,3;

Ответы:

а) 0,8 : 0,2 = 8 : 2 = 4

б) 0,126 : 0,3 = 0,42

-1,26 3

12 0,42

- 6

6

0

Задание 3. Найдите значение выражения.

а) 24,5 : 3,5 1,2; б) 0,824 : 0,8 0,3;

Ответы:

а) 24,5 : 3,5 1,2 = 8,4

1) 24,5 : 3,5 = 7

- 245 35

245 7

0

2) 7 1,2 = 8,4

1,2

* 7

8,4

б) 0,824 : 0,4 0,6 = 1,236

1) 0,824 : 0,4 = 2,06

- 8,24 4

8 2,06

- 24

24

0

2) 2,06 0,6 = 1,236

2,06

* 0,6

1,236

Задача 1.

Найдите сумму площадей стен классов в школе, длина которых 8,6 м, ширина 4,5 м и высота 2,91 м. Найдите объем класса. Ответы округлите до десятых.

Решение.

1. 4,5+8,6 = 13,1 (м) – сумма длины и ширины класса

2. 26,2 2,91 = 76,242 = 76,2 (м²) – сумма площадей стен класса

26,2

* 2,91

262

+ 2358

524

76,242

1. 8,6 4,5 2,91 =112,617 = 112,6 (м³) – объем класса

8,6

* 4,5

430

+ 344

38,70

38,7

* 2,91

387

+ 3483

774

112,617

Ответ. сумма площадей стен комнаты 76,2 м², объем комнаты 112,6 м³.

Задача 2. Веревку разрезали на две части. Длина одной части 4,25 м, а длина другой части в 1,6 раза меньше первой. Какова была длина веревки?

Решение.

1. 4,25 : 1,6 = 2,65625 (м)

-42,5 16

32 2,65625

-105

96

- 90

80

-100

96

-40

32

-80

80

0

1. 2,65625 + 4,25 = 6,90625 (м)

Ответ. 6,90625 м

Задача 3. На приготовление уроков Ваня затратил в 2,5 раза меньше времени, чем на прогулку. Но на поход с родителями в магазин, он затратил в 3,5 раза больше времени, чем на прогулку. Сколько времени ушло у Вани на прогулку, поход в магазин и приготовление уроков, если прогулка заняла 1,2 ч?

Решение.

1. 1,2 : 2,5 = 0,48 (ч) – заняло приготовление уроков

- 120 25

100 0,48

- 200

200

0

1. 1,2 3,5 = 4,2 (ч) – занял поход в магазин

1,2

* 3,5

60

+ 36

4,20

1. 0,48 + 4,2 + 1,2 = 5,88 (ч)

Ответ. 5,88 ч

Рефлексивно – оценочная часть

1. Какова была цель урока? (Рассмотреть, как правила умножения и деления десятичных дробей используются при решении различных задач)

2. Достигли мы её? (Да)

3. Как мы её достигли? (Рассмотрели различные задачи: задачи на нахождение площади, объема, скорости, пути)

Домашняя работа. Задача № 1411, № 1452.

Ответы:

Задача №1411.(учебник)

Площадь одного поля 207, 5 га, а площадь второго на 17 га больше. Сколько пшеницы собрали с обоих полей, если с каждого гектара первого поля собирали 32,4 ц, а с каждого гектара второго – 28,6 ц? Ответ округлите до целых.

Решение.

1. 207,5 + 17 = 224,5 (га) – площадь второго поля

2. 207,5 32,4 = 6723 (ц) – собрали с 1 поля

207,5

* 32,4

8300

+ 4150

6225

6723,00

1. 224,5 28,6 = 6330,7 (ц) – собрали с 2 поля

224,5

* 28,6

13470

+ 17960

4490

6420,70

1. 6723 + 6330,7 = 13143,7 13143 (ц)

Ответ. 13143 ц пшеницы собрали с обоих полей.

Задача №1452.(учебник) В первый пакет вошло 6,72 кг муки, что в 2,4 раза больше, чем во второй пакет. Сколько килограммов муки вошло в оба пакета?

Решение.

1. 6,72 : 2,4 = 2,8 (кг) – вошло муки во второй пакет

- 67,2 24

48 2,8

- 192

192

0

1. 6,72 + 2,8 = 9,52 (кг) – вошло муки в оба пакета

Ответ. 9,52 кг