ПЛАН-КОНСПЕКТ УРОКА
Тема урока: ТЕОРЕМА ПИФАГОРА
ФИО автора: Ахметхафизова Альфия Амирзагитовна
Место работы МОБУ СОШ с.Старокуручево муниципального района Бакалинский район Республики Башкортостан
Должность: Учитель
Предмет: Геометрия
Класс: 8 класс, уровень знаний учащихся - средний.
Тема и номер урока в теме: Теорема Пифагора, первый урок по теме
Базовый учебник: Погорелов А.В. Геометрия. Учебник для 7-9 классов
Цель и задачи урока: формировать и совершенствовать навыки решения прямоугольных треугольников.
Образовательные: формирование знаний теоремы Пифагора, умений доказывать теорему и применять ее в решении задач; формирование умений решать прямоугольные треугольники.
Воспитательные: воспитывать ответственное отношение к учебному труду; аккуратность в процессе оформления решения задач и доказательства теоремы; воспитание дисциплинированности на уроке.
Развивающие: развитие памяти учащихся; умений преодолевать трудности при решении математических задач; познавательного интереса учащихся; развитие культуры устной и письменной речи.
Тип урока: урок «открытия» нового материала.
Форма работы учащихся: фронтальная, групповая, индивидуальная
Необходимое техническое оборудование: мультимедиапроектор; карточки с тестами для повторения изученного, энциклопедии и рефераты учащихся, презентация «Теорема Пифагора», шаржи к теореме; портрет Пифагора, таблица «Теорема Пифагора»
СТРУКТУРА И ХОД УРОКА
| № | Этап урока | Деятельность учителя (с указанием действий с ЭОР, например, демонстрация) | Деятельность ученика | Время (в мин) |
| | Организационный этап | Постановка цели урока: Учитель: Сегодня на уроке мы продолжим изучать свойства прямоугольного треугольника. Я вас познакомлю с одной из основных теорем геометрии, которая позволит вам решать новые интересные задачи и доказывать новые теоремы в геометрии. А для доказательства этой теоремы потребуются знания,полученные на предыдущих уроках, качество знаний вы продемонстрируете выполнив самостоятельно небольшой тест в течении 3 минут | Настраиваются на работу | 1 мин |
| 2 | Актуализация опорных знаний | Подготовка к изучению нового материала Тестирование №1. Дан прямоугольный треугольник МРК. а) Назовите катеты___________ гипотенузу _______
б) Чему равен: cos M=_________
cos P=__________
10 6 К 8 Р №2. В прямоугольном треугольнике катет равен 6 см, а косинус прилежащего угла равен 0,6. Чему равна гипотенуза? №3. В прямоугольном треугольнике гипотенуза равна 10 см, а косинус одного из острых углов равен 0,6. Чему равен катет, прилежащий к острому углу? №4. В прямоугольном треугольнике АВС проведена высота СЕ. Е С В
Выразите: 1) cos В=__________ 2) 3) Самопроверка работы с помощью мультимедиапроектора, с параллельным комментированием. Норма оценки: «5» нет ошибок «4»- 1-2аналогичныеошибки «3» - 3-4аналогичныеошибки «2» - более 4 ошибок | На заранее розданных листочках с тестом ученики выполняют работу. Учащиеся проверяют свои работы и оценивают их. Тесты передают учителю. | 5 мин
|
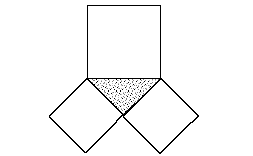
| 3 | Этап мотивации | 3. Ознакомление с новым материалом Сегодня на уроке мы приступаем к изучению одной из важнейших теорем геометрии – теоремы Пифагора. Она является основой решения множества геометрических задач и базой изучения теоретического материала в дальнейшем. Докажем эту теорему и решим несколько задач с её применением, но сначала послушаем рассказ о математике, именем которого она названа, его подготовил… « ПИФАГОР САМОССКИЙ (ок. 580 – ок. 500 г. до н.э.) Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. Ещё в детстве он проявлял незаурядные способности, и когда подрос, неугомонному воображению юноши стало тесно на маленьком острове. Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет, где сам, когда-то изучал науки. Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги были в образе людей, а египетские боги – в образе полулюдей-полуживотных. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с многовековыми достижениями египетской науки. Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать. С большим трудом ему удалось преодолеть эту преграду. Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Наука Вавилона была более развитой, нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при сёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений. Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Кротоне. Там Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю. Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе: 1) теорема о сумме внутренних углов треугольника; 2) построение правильных многоугольников и деление плоскости на некоторые из них; 3) геометрические способы решения квадратных уравнений; 4) деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел; 5) доказательство того, что 2 не является рациональным числом; 6) создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое. Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев. Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания. После его смерти ученики окружили имя своего учителя множеством легенд.» -Ребята, знаете ли вы что-нибудь связанное с именем Пифагора? Пифагор сделал много важных открытий, но наибольшую славу ученому принесла доказанная им теорема, которая сейчас носит его имя. Откройте тетради, запишите число…. И тему урока «Теорема Пифагора» В современных учебниках теорема сформулирована так: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов». Предполагают, что во времена Пифагора теорема звучала по-другому:«Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах». Вероятно факт, изложенный в теореме Пифагора, был сначала установлен для равнобедренных прямоугольных треугольников. Квадрат построенный на гипотенузе, содержит 4 треугольника. А на каждом катете построен квадрат содержащий 2 треугольника. Из рисунка видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах. Смотрите, а вот и «Пифагоровы штаны во все стороны равны» Такие стишки придумывали учащиеся средних веков при изучении теоремы, а так же рисовали шаржи, которые дошли и до нас. Теорема Пифагора имеет богатую историю. Оказывается, она задолго до Пифагора была известна в Египте, Китае, Индии. За восемь веков до нашей эры эта теорема была хорошо известна индийцам под названием «правила веревки» и использовалась ими для строительства алтарей. Доказательство самого Пифагора до нас не дошло. В настоящее время насчитывается свыше 100 различных доказательств теоремы Пифагора. Возможно, что одно из них принадлежит Пифагору или его ученику. Те кто заинтересуется доказательством теоремы могут познакомиться и с другими доказательствами по книгам, газете, рефератам, которые приготовили для нас учащиеся.
| Учащиеся формулируют теорему, игра «Пифагор», стихотворение о Пифагоровых штанах…
| 5 мин |
| 4 | Изучение нового материала | -Итак, докажем теорему Пифагора в современной формулировке. - Начертите прямоугольный треугольник АВС с прямым углом С. - Что дано по условию теоремы? - Что необходимо доказать? | Анализируют доказательство теоремы Пифагора, проговаривают формулировку теоремы, выполняют доказательство в тетрадях: С А B Дано: Доказать: АВ2= АС2+СВ2. | 10 мин |
| 5 | Первичное применение знаний | Учитель предлагает выполнить задания из электронного практикума. | Учащиеся выполняют задания | 10 мин |
| 6 | Контроль и самопроверка знаний | Учащимся, испытывающим затруднения учитель оказывает помощь. | Осуществляют самоконтроль | 10 мин |
| 7 | Подведение итогов, рефлексия | Подводит итоги по самостоятельной работе. Предлагает учащимся оценить свою деятельность на уроке | Выставляют оценки | 2 мин |
| 8 | Подача домашнего задания | Постановка домашнего задания и его комментирование: объявляет номера – обязательные и для дополнительного изучения
| Записывают задания домашней работы, задают вопросы | 2 мин |
ПЕРЕЧЕНЬ ИСПОЛЬЗУЕМЫХ НА ДАННОМ УРОКЕ ЭОР
| № | Название ресурса | Тип, вид ресурса | Форма предъявления информации | Гиперссылка на ресурс, обеспечивающий доступ к ЭОР |
| 1 | ЭОР 1 | информационный | лекция | http://school-collection.edu.ru/catalog/res/7383a6e4-0dac-11dc-8314-0800200c9a66/view/ |
| 2 | ЭОР 2 | практический |
| http://fcior.edu.ru/card/10274/teorema-pifagora.html# |
| 3 | ЭОР 3 | контролирующий |
| http://school-collection.edu.ru/catalog/res/188f3053-0ed2-4d55-8a41-297b97cb417f/view/ |
| 4 | ЭОР 4 | информационный | лекция | :http://school-collection.edu.ru/catalog/res/648d87e8-0b93-39b7-bf79-498944b4ff26/view/ |

 Получите свидетельство
Получите свидетельство Вход
Вход



 М
М А
А 

 О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским.
О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским. 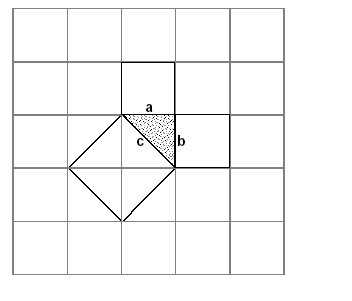









 Конспект урока по теме "Теорема Пифагора" (218.5 KB)
Конспект урока по теме "Теорема Пифагора" (218.5 KB)
 0
0 207
207 9
9 Нравится
0
Нравится
0


