Предмет: астрономия
Учитель: Кузина Маргарита Викторовна, МБОУ «Гимназия № 11 г. Ельца»
Уровень образования: базовый
Тема: « Определение расстояний и размеров тел в Солнечной системе»
Тип урока: изучение и первичное закрепление новых знаний и способов деятельности.
Время проведения: 1 полугодие
Участники: 11Б
Цель: Познакомить с различными способами определения расстояний до небесных тел Солнечной системы.
Образовательные задачи урока:
Вычисление расстояний до небесного тела Солнечной системы.
Решение задачи на определение расстояний
Совершенствование работы с подвижной картой звездного неба.
Развивающие задачи урока:
Формирование умения подбора литературы, выделения главного из отобранного материала
Развитие творческих способностей обучающихся
Воспитательные задачи урока:
Формирование активного отношения у изучению материала
Содействие формированию мировоззренческой идеи о познаваемости мира.
Оборудование:
техническое оснащение: компьютер, мультимедийный проектор, компакт диск с записью музыки
наглядные пособия: демонстрационная карта звёздного неба, подвижные карты звёздного неба (у каждого ученика)
программное обеспечение:программы Microsoft Word, Photoshop, Power Point, Internet Explorer.
Ключевые слова: триангуляция, параллактическое смещение, горизонтальный параллакс, радиолокация, астрономическая единица
Литература:
Астрономия. Базовый уровень. 11 класс: учебник/ Б.А. Воронцов-Вельяминов, Е.К.Страут. – М.: Дрофа, 2018. – 238.
Астрономия. 11 класс. Методическое пособие к учебнику Б.А. Воронцова-Вельяминова, Е.К.Страута «Астрономия. Базовый уровень. 11 класс»/ М.А.Кунаш. – М.: Дрофа, 2018, 217с.
Астрономия. 11 класс: поурочные планы по учебнику Е.П.Левитана, - Волгоград: Учитель, 2007
Аннотация Межпредметная связь: Градусная и радианная меры угла, смежные и вертикальные углы. Шар и сфера (математика, 5, 7, 10, 11 кл.). Расстояние от Земли до Луны и Солнца. Сравнительные размеры Солнца и Земли, Земли и Луны (природоведение, 5 кл). Скорость распространения электромагнитных волн. Метод радиолокации (физика, 11 кл).
Длительность урока: 45 мин.
План урока.
Орг. момент
Постановка целей и задач.
Изучение нового материала
сообщения учащихся,
решение задач,
работа с презентацией
Закрепление новых знаний
проверка усвоения материала,
работа с подвижной картой звездного неба
Д.з. Итог урока
Ход урока.
Организационный момент.
Постановка целей и задач.
Сегодня на уроке мы:
Поговорим о форме и размерах Земли;
Узнаем, как Эратосфен измерил радиус Земли
Рассмотрим способы измерения больших расстояний
Для этого вы:
прослушаете сообщения одноклассников
просмотрите презентацию
решите задачи
определите место планеты на подвижной карте звездного неба.
Изучение нового материала
Эпиграфом к нашему уроку я взяла четверостишие
Вот дотошные наши земляне!
Всё измерить бы нам, рассчитать.
И от центра Земли расстоянье
К центру Солнца сумели узнать.
Используя третий закон Кеплера, среднее расстояние всех планет от Солнца можно выразить через среднее расстояние Земли от Солнца. Определив его в километрах, можно найти в этих единицах все расстояния в Солнечной системе.
Но есть и другие варианты. Разобраться в этом нам помогут сообщения, подготовленные одноклассниками
Градусные измерения и триангуляция
Эратосфен — греческий ученый, живший в египетском городе Александрии с 276 года по 196 год до нашей эры. Работал он в Александрийском мусейоне. Отчасти это был музей, отчасти научный центр того времени.
т проезжих путешественников Эратосфен услышал о необычном явлении, которое они наблюдали в Сиене, городе, расположенном далеко к югу от Александрии. Путешественники рассказали, что в полдень первого дня лета — в самый тельный день в году — в Сиене исчезали тени. Солнце в это время стояло прямо над головой, лучи его падали на землю отвесно вниз. Внимательно вглядываясь в воду водоема, можно было рассмотреть отражение Солнца на дне.
Э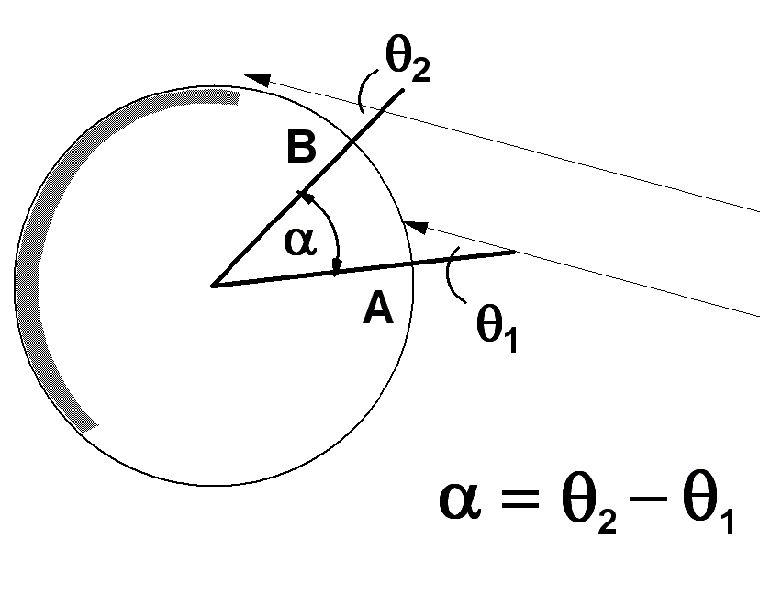 ратосфен съездил в Сиену и убедился в этом сам. Вернувшись в Александрию, он обнаружил, что и в самый длительный день года в полдень стены мусейона продолжали отбрасывать тень на землю. Основываясь на этом простом наблюдении, он смог вычислить окружность Земли.
ратосфен съездил в Сиену и убедился в этом сам. Вернувшись в Александрию, он обнаружил, что и в самый длительный день года в полдень стены мусейона продолжали отбрасывать тень на землю. Основываясь на этом простом наблюдении, он смог вычислить окружность Земли.
Вычисления окружности Эратосфен знал, что из - за громадного расстояния от Земли до Солнца, лучи последнего достигают и Сиены и Александрии параллельными лучами. То есть лучи Солнца, падающие на землю в Александрии, параллельны лучам, падающим на землю в Сиене в то же время. Если бы Земля была плоской, то тени исчезали бы на ней повсеместно 21 июня. Но так как, рассуждал он, Земля искривлена, то в Александрии, удаленной от Сиены на 500 миль (1 миля равна 1,609 километра) к северу, местные стены и колонны наклонены по отношению к сиенским стенам и колон нам под некоторым углом. Итак, в полдень первого дня лета Эратосфен измерил тень, отбрасываемую обелиском, стоявшим неподалеку от мусейона. Зная высоту обелиска, он смог легко вычислить длину линии, соединяющей вершину обелиска и конец тени. Получился воображаемый треугольник. После того как треугольник был «очерчен», оставалось, используя известные к тому времени правила геометрии, вычислить его углы. И Эратосфен их вычислил. Он нашел, что угол отклонения обелиска от солнечного луча составляет чуть больше 7 градусов. Так как в Сиене вертикальные предметы не отбрасывали тени, то угол между ними и солнечным лучом составлял ноль градусов. Короче, никакого угла не было. Это означало, что Александрия отстоит по земной окружности от Сиены на 7 градусов. Такой угол между городами — это 1/50 часть окружности. Всякая окружность содержит 360 градусов, земная окружность в этом смысле не исключение. Эратосфен умножил расстояние между Сиеной и Александрией — 500 миль — на 50 и получил значение окружности Земли. Оно оказалось равным 25 тысячам миль. Современные ученые, измерившие с помощью высококлассной техники окружность Земли, нашли ее равной 24 894 тысяч миль. Все таки Эратосфен оказался первоклассным ученым, а не дилетантом.
Источник: http://www.voprosy-kak-i-pochemu.ru/eratosfen-i-okruzhnost-zemli/ .
П
 араллактическое смещение
араллактическое смещение
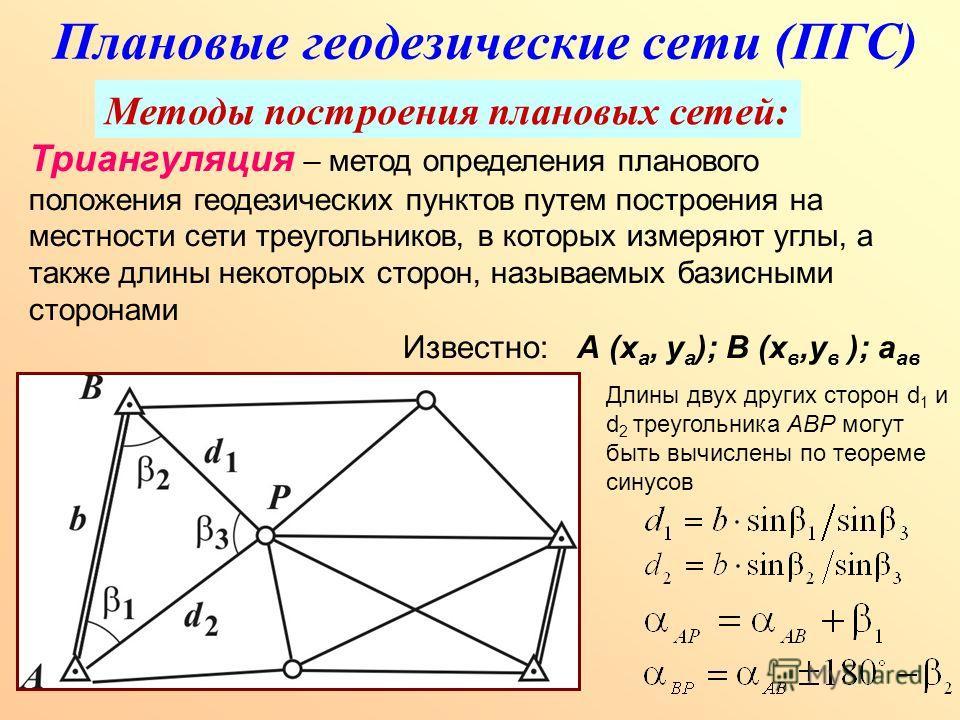
Классическим способом определения расстояний был и остается угломерный геометрический способ. Им определяют расстояния и до далеких звезд, к которым метод радиолокации неприменим. Геометрический способ основан на явлении параллактического смещения. Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя
3)Объяснение учителя
а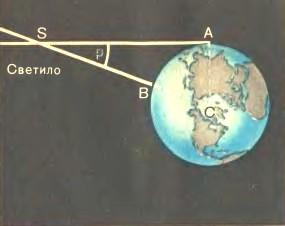 ) Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда впервые был определен горизонтальный параллакс Солнца. Угол, под которым со светила виден радиус Земли, перпендикулярный к лучу зрения, называется горизонтальным параллаксом.
) Измерить расстояние от Земли до Солнца удалось лишь во второй половине XVIII в., когда впервые был определен горизонтальный параллакс Солнца. Угол, под которым со светила виден радиус Земли, перпендикулярный к лучу зрения, называется горизонтальным параллаксом.
D=R/sin p
1 рад = 206265’’
При малых углах sin р = p, если угол р выражен в радианах. Если р выражен в секундах дуги, то вводится множитель
![]()
где 206265 — число секунд в одном радиане.
Тогда
![]()
Знание этих соотношений упрощает вычисление расстояния по известному параллаксу:
![]()
б) Определение размеров тел
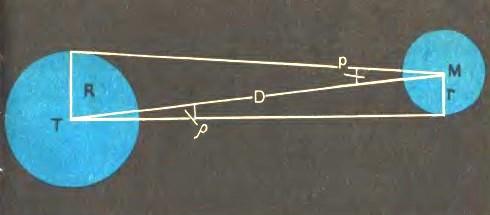
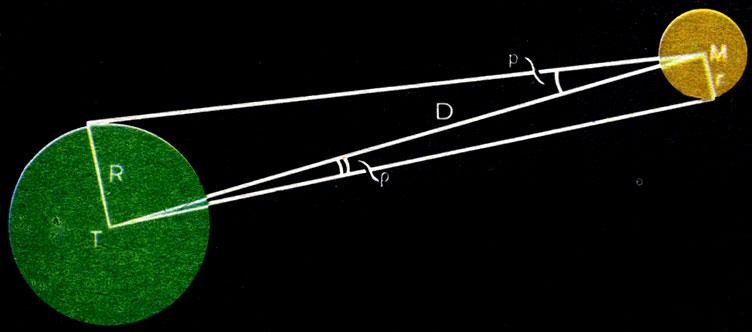
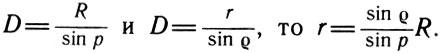
Если углы ![]() и ρ малы, то синусы пропорциональны углам, и можно написать:
и ρ малы, то синусы пропорциональны углам, и можно написать:
![]()
Этот способ определения размеров светил применим только тогда, когда виден диск светила.
в) С 40-х годов нашего века радиотехника позволила определять расстояния до небесных тел посредством радиолокации, о которой вы знаете из курса физики. Советские и американские ученые уточнили радиолокацией расстояния до Меркурия, Венеры, Марса и Юпитера.
Закрепление новых знаний
упр 11 (1)
Чему равен горизонтальный параллакс Юпитера, наблюдаемого с Земли в противостоянии, если Юпитер в 5 раз дальше от Солнца, чем Земля?
Д.з. Итог урока
п 13, упр. 11 (2, 4)
Заполните таблицу
| Цель | Требуемые параметры (что нужно знать для достижения поставленной цели) |
| Вычисление радиуса Земли |
|
| Вычисление расстояния до тела Солнечной системы |
|
Д.з.
http://tepka.ru/astronomiya
Пример решения задачиЗадача. На каком расстоянии от Земли находится Сатурн, когда его горизонтальный параллакс равен 0,9"?

Зная расстояние D до светила и измерив его угловой радиус ![]() , можно вычислить его линейный радиус r: r=Dsin
, можно вычислить его линейный радиус r: r=Dsin![]() или r=D
или r=D![]() , если угол
, если угол ![]() выражен в радианах.
выражен в радианах.
Задача. Чему равен линейный диаметр Луны, если она видна с расстояния 400 000 км под углом примерно 0,5°?

1. Закончите предложения
Для измерения расстояний в пределах Солнечной системы используют астрономическую единицу (а. е.), которая равна среднему расстоянию от Земли до Солнца.
1 а.е. = 149 600 000 км
Расстояние до объекта по времени прохождения радиолокационного сигнала можно определить по формуле , где S = 1/2·ct, где S — расстояние до объекта, c — скорость света, t — время прохождения светила.
2. Дайте определения понятиям «параллакс» и «базис»; на рисунке 10.1 покажите эти величины
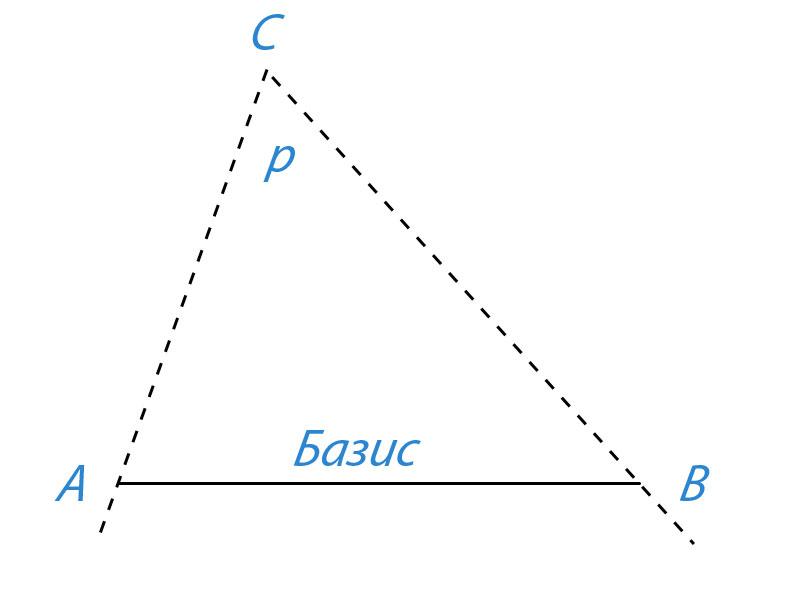
Параллакс — угол p, под которым из недоступного места (точка C) будет виден отрезок AB, называемый базисом.
Базис — тщательно измеренное расстояние от точки A (наблюдатель) до какой-либо достигнутой для наблюдения точки B.
3. Как с помощью понятий параллакса и базиса определить расстояние до удаленного недоступного объекта С (рис. 10.1)?
По величине базиса и прилегающим к нему углам треугольника ABC найти расстояние AC. При измерениях на Земле этот метод называют триангуляцией.
4. Угол, под которым со светила S виден радиус Земли, перпендикулярный лучу зрения, называется горизонтальным параллаксом p (рис, 10.2). Определите расстояния: а) до Луны, если ее горизонтальный параллакс p = 57′; б) до Солнца, горизонтальный параллакс которого p = 8,8″
Решение.
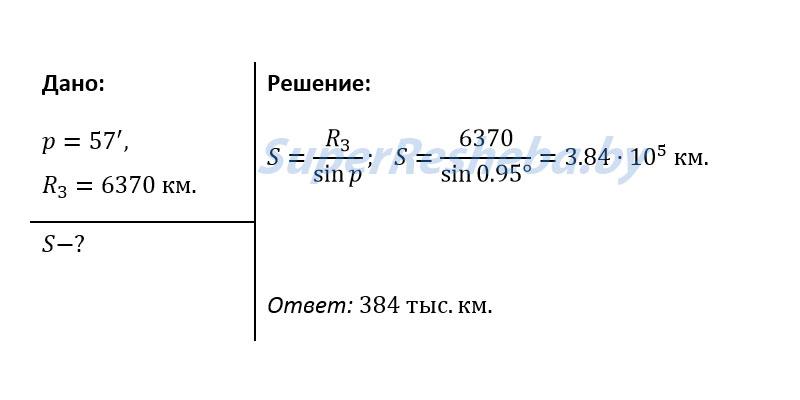
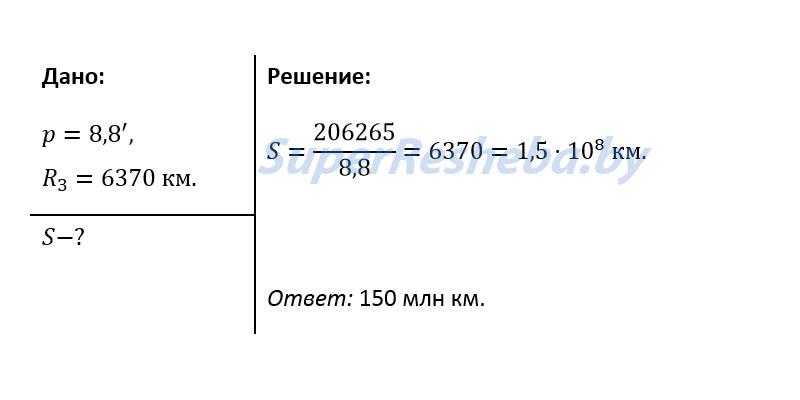
Вариант 2.
1. Сигнал, посланный радиолокатором к Венере, возвратился назад через t — 4 мин 36 с. На каком расстоянии в это время находилась Венера в своем нижнем соединении?
Ответ: 41 млн км.
2. На какое расстояние к Земле подлетал астероид Икар, если его горизонтальный параллакс в это время был p = 18,0″?
Ответ: 1,22 млн км.
3. С помощью наблюдений определили, что угловой радиус Марса p = 9,0″, а горизонтальный параллакс p = 16,9″. Определите линейный радиус Марса.
Ответ: 3390 км.
http://superresheba.by
I. Опрос учащихся (5-7 минут). Диктант.
Ученый, создатель гелиоцентрической системы мира. (Н. Коперник)
Ближайшая точка орбиты ИСЗ. (Перигей)
Значение астрономической единицы. (1 а. е.=149600000км )
Основные законы небесной механики. (4 закона-3Вт и 3-й закон Коперника)
Планета, открытая на «кончике пера». (Нептун)
Значение круговой (I космической) скорости для Земли. (7,9 км/с)
Отношение квадратов периодов обращения двух планет равно 8. Чему равно отношение больших полуосей этих планет? (2)
В какой точке эллиптической орбиты ИСЗ имеет минимальную скорость? (В апогее)
Немецкий астроном, открывший законы движения планет (И. Кеплер)
Формула третьего закона Кеплера, после уточнения И. Ньютона.
Вид орбиты межпланетной станции, посланной для облета Луны. (Эллипс)
Чем отличается первая космическая скорость от второй. (в
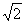 раз )
раз )В какой конфигурации находится Венера, если она наблюдается на фоне диска Солнца? (Соединение нижнее)
В какой конфигурации Марс ближе всего к Земле. (В противостоянии)
Виды периодов движения Луны = (временных)? (Сидерический, синодический).
II Новый материал
1) Определение расстояний до небесных тел.
В астрономии нет единого универсального способа определения расстояний. По мере перехода от близких небесных тел к более далеким одни методы определения расстояний сменяют другие, служащие, как правило, основой для последующих. Точность оценки расстояний ограничивается либо точностью самого грубого из методов, либо точностью измерения астрономической единицы длины (а. е.).
1-й способ: (известен) По третьему закону Кеплера можно определить расстояние до тел СС, зная периоды обращений и одно из расстояний. 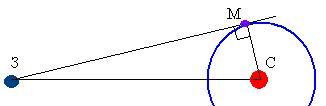
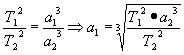 Приближённый метод.
Приближённый метод.
2-й способ: Определение расстояний до Меркурия и Венеры в моменты элонгации (из прямоугольного треугольника по углу элонгации).
3-й способ: Геометрический (параллактический).
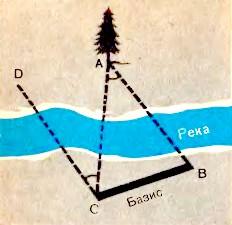
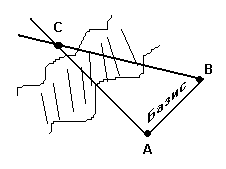 Пример: Найти неизвестное расстояние АС.
Пример: Найти неизвестное расстояние АС.
[АВ] – Базис - основное известное расстояние, т. к. углы САВ и СВА – известны, то по формулам тригонометрии (теорема синусов) можно в ? найти неизвестную сторону, т. е. [CА]. Параллактическим смещением называется изменение направления на предмет при перемещении наблюдателя.
Параллакс- угол (АСВ), под которым из недоступного места виден базис (АВ - известный отрезок). В пределах СС за базис берут экваториальный радиус Земли R=6378км.
Пусть К - местонахождение наблюдателя, из которого светило видно на горизонте. Из рисунка видно, что из прямоугольного треугольника гипотенуза, расстояние D равно: , так как при малом значении угла если выражать величину угла в радианах и учитывать, что угол выражен в секундах дуги, а 1рад =57,30=3438'=206265", то и получается вторая формула.
Угол (ρ) под которым со светила, находящегося на горизонте (? R - перпендикулярно лучу зрения) был бы виден экваториальный радиус Земли называется горизонтальным экваториальным параллаксом светила.
Т.к. со светила никто наблюдать не будет в силу объективных причин, то горизонтальный параллакс определяют так:
измеряем высоту светила в момент верхней кульминации из двух точек земной поверхности, находящихся на одном географическом меридиане и имеющем известные географические широты.
из полученного четырехугольника вычисляют все углы (в т. ч. параллакс).
Из истории: Первое измерение параллакса (параллакса Луны) сделано в 129г до НЭ Гиппархом (180-125, Др. Греция).
Впервые расстояния до небесных тел (Луны, Солнца, планет) оценивает Аристотель (384-322, Др. Греция) в 360г до НЭ в книге «О небе» →слишком не точно, например радиус Земли в 10000 км.
В 265г до НЭ Аристарх Самосский (310-230, Др. Греция) в работе «О величине и расстоянии Солнца и Луны» определяет расстояние через лунные фазы. Так расстояния у него до Солнца (по фазе Луны в 1 четверти из прямоугольного треугольника, т. е. впервые использует базисный метод: ЗС=ЗЛ/cos 87º≈19*ЗЛ). Радиус Луны определил в 7/19 радиуса Земли, а Солнца в 6,3 радиусов Земли (на самом деле в 109 раз). На самом деле угол не 87º а 89º52' и поэтому Солнце дальше Луны в 400 раз. Предложенные расстояния использовались многие столетия астрономами.
В 240г до НЭ ЭРАТОСФЕН (276-194, Египет) произведя измерения 22 июня в Александрии угла между вертикалью и направлением на Солнце в полдень (считал, что раз Солнце очень далеко, то лучи параллельны) и используя записи наблюдений в тот же день падения лучей света в глубокий колодец в Сиене (Асуан) (в 5000 стадий = 1/50 доли земной окружности (около 800км) т. е. Солнце находилось в зените) получает разность углов в 7º12' и определяет размер земного шара, получив длину окружности шара 39690 км (радиус=6311км). Так была решена задача определения размера Земли, используя астрогеодезический способ. Результат не был произведён до 17 века, лишь астрономы Багдадской обсерватории в 827г немного поправили его ошибку.
В 125г до НЭ Гиппарх довольно точно определяет (в радиусах Земли) радиус Луны (3/11 R⊕) и расстояние до Луны (59 R⊕).
Точно определил расстояние до планет, приняв расстояние от Земли до Солнца за 1а.е., Н. Коперник.
Наибольший горизонтальный параллакс имеет ближайшее тело к Земле - Луна. Р?=57'02"; а для Солнца Р=8,794"
Задача 1: учебник Пример № 6 - Найти расстояние от Земли до Луны, зная параллакс Луны и радиус Земли.
Задача 2 : (самостоятельно). На каком расстоянии от Земли находится Сатурн, если его параллакс 0,9". [из формулы D=(206265/0,9)*6378= 1461731300км = 1461731300/149600000≈9,77а.е.]
4-й способ Радиолокационный: импульс→объект →отраженный сигнал→время. Предложен советскими физиками Л.И. Мандельштам и Н.Д. Папалекси. Быстрое развитие радиотехники дало астрономам возможность определять расстояния до тел Солнечной системы радиолокационными методами. В 1946г была произведена первая радиолокация Луны Баем в Венгрии и в США, а в 1957-1963гг — радиолокация Солнца (исследования солнечной короны проводятся с 1959г), Меркурия (с 1962г на = 3.8, 12, 43 и 70 см), Венеры, Марса и Юпитера (в 1964 г. на волнах = 12 и 70 см), Сатурн (в 1973 г. на волне = 12.5 см) в Великобритании, СССР и США. Первые эхо-сигналы от солнечной короны были получены в 1959 (США), а от Венеры в 1961 (СССР, США, Великобритания). По скорости распространения радиоволн с = 3 105 км/сек и по промежутку времени t (сек) прохождения радиосигнала с Земли до небесного тела и обратно легко вычислить расстояние до небесного тела.VЭМВ=С=299792458м/с≈3*108 м/с.
Основная трудность в исследовании небесных тел методами радиолокации связана с тем, что интенсивность радиоволн при радиолокации ослабляется обратно пропорционально четвертой степени расстояния до исследуемого объекта. Поэтому радиолокаторы, используемые для исследования небесных тел, имеют антенны больших размеров и мощные передатчики. Например, радиолокационная установка центра дальней космической связи в Крыму имеет антенну с диаметром главного зеркала 70 м и оборудована передатчиком мощностью несколько сотен кВт на волне 39 см. Энергия, направляемая к цели, концентрируется в луче с углом раскрыва 25'.
Из радиолокации Венеры, уточнено значение астрономической единицы: 1 а. е.=149 597 870 691 ± 6м ≈149,6 млн.км., что соответствует Р=8,7940". Так проведенная в Советском Союзе обработка данных радиолокационных измерений расстояния до Венеры в 1962-75гг (один из первых удачных экспериментов по радиолокации Венеры провели сотрудники Института радиотехники и электроники АН СССР в апреле 1961г антенной дальней космической связи в Крыму, = 39 см) дала значение 1 а.е. =149597867,9 ±0,9 км. XVI Генеральная ассамблея Международного астрономического союза приняла в 1976г значение 1 а.е.=149597870±2 км. Путем радиолокации с КА определяется рельеф поверхности планет и их спутников, составляются их карты.
Основные антенны, используемые для радиолокации планет:
= Евпатория, Крым, диаметр 70 м, = 39 см;
= Аресибо, Пуэрто Рико, диаметр 305 м, = 12.6 см;
= Голдстоун, Калифорния, диаметр 64 м, = 3.5 и 12.6 см, в бистатическом режиме прием осуществляется на системе апертурного синтеза VLA.
С изобретение Квантовых генераторов (лазера) в 1969г произведена первая лазерная локация Луны (зеркало для отражения лазерного луча на Луне установили астронавты США «Ароllо - 11» 20.07.69г), точность измерения составили ±30 см. На рисунке показано расположение лазерных уголковых отражателей на Луне, установленных при полете КА "Луна-17, 21" и "Аполлон - 11, 14, 15". Все, за исключением отражателя Лунохода-1 (L1), работают и сейчас.
Лазерная (оптическая) локация нужна для:
-решение задач космических исследований.
-решение задач космической геодезии.
-выяснения вопроса о движении земных материков и т.д.
2) Определение размеров небесных тел.
а) Определение радиуса Земли.
| АОВ=n=φА-φВ(разность географических широт) Аналогичным способом в 240г до НЭ (рисунок выше) определяет радиус Земли географ Эратосфен. L/800=3600/7,20 |
б) Определение размера небесных тел.
|
| Р- параллакс. |
III. Закрепление материала
Пример 7 (стр. 51).
CD- "Red Shift 5.1" - Определить на данный момент удаленность нижних (планет земной группы, верхних планет, планет гигантов) от Земли и Солнца в а.е.
Угловой радиус Марса 9,6", а горизонтальный параллакс 18". Чему равен линейный радиус Марса? [Из формулы 22 получим 3401,6 км. (фактически 3396 км)].
Каково расстояние между лазерным отражателем на Луне и телескопом на Земле, если импульс возвратился через 2,43545с? [ из формулы R=(c.t)/2 R=3.108.2,43545/2≈365317500,92м≈365317,5км]
Расстояние от Земли до Луны в перигее 363000км, а в апогее 405000км. Определите горизонтальный параллакс Луны в этих положениях. [ из формулы D=(206265"/p)*R⊕ отсюда р=(206265"/D)*R⊕; рА=(206265"/405000)*6378≈3248,3"≈54,1', рП= (206265"/363000)*6378≈3624,1"≈60,4'].
Тест с картинками по главе 2.
Дополнительно, для тех кто сделал - кроссворд.
|
Итог:
1) Что такое параллакс?
2) Какими способами можно определить расстояние до тел СС?
3) Что такое базис? Что принимается за базис для определения расстояния до тел СС?
4) Как зависит параллакс от удаленности небесного тела?
5) Как зависит размер тела от угла?
6) Оценки
Домашнее задание: §11; вопросы и задания стр. 52, стр. 52-53 знать и уметь. Повторить полностью вторую главу. СР№6, ПР№4.
Можно задать по данному разделу подготовить кроссворд, опросчик, реферат об одном из ученых-астрономов или истории астрономии (один из вопросов или направлений).
Можно предложить практическую работу "Определение размера Луны".
В период полнолуния, используя две соединенные под прямым углом линейки, определяются видимые размеры лунного диска: поскольку треугольники KCD и КАВ подобны, из теоремы о подобии треугольников следует, что: АВ/СD=KB/KD. Диаметр Луны АВ = (CD.KB)/KD. Расстояние от Земли до Луны берёте из справочных таблиц (но лучше, если сумеете вычислить его сами).
http://www.astro.websib.ru/metod/tem-2/

 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока по астрономии: "Определение растояний и размеров тел в Солнечной системе" (603 KB)
Конспект урока по астрономии: "Определение растояний и размеров тел в Солнечной системе" (603 KB)
 0
0 3362
3362 136
136 Нравится
0
Нравится
0


