Получите свидетельство
Вход
Тема: Перпендикулярность прямых и плоскостей
Урок: Прямоугольный параллелепипед
1. Определение параллелепипедаПоверхность, составленная из двух равных параллелограммов АВСD и А1В1С1D1 и четырех параллелограммов АВВ1А1, ВСС1В1, СDD1С1, DАА1D1, называется параллелепипедом (рис. 1).
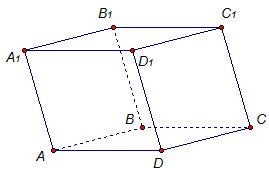
Рис. 1 Параллелепипед
То есть: имеем два равных параллелограмма АВСD и А1В1С1D1 (основания), они лежат в параллельных плоскостях так, что боковые ребра АА1, ВВ1, DD1, СС1 параллельны. Таким образом, составленная из параллелограммов поверхность называется параллелепипедом.
Таким образом, поверхность параллелепипеда - это сумма всех параллелограммов, из которых составлен параллелепипед.
2. Свойства параллелепипеда1. Противоположные грани параллелепипеда параллельны и равны.
(фигуры равны, то есть их можно совместить наложением)
Например:
АВСD = А1В1С1D1 (равные параллелограммы по определению),
АА1В1В = DD1С1С (так как АА1В1В и DD1С1С – противоположные грани параллелепипеда),
АА1D1D = ВВ1С1С (так как АА1D1D и ВВ1С1С – противоположные грани параллелепипеда).
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Диагонали параллелепипеда АС1, В1D, А1С, D1В пересекаются в одной точке О, и каждая диагональ делится этой точкой пополам (рис. 2).
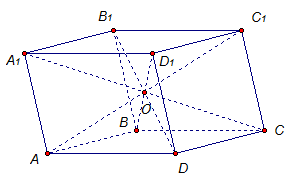
Рис. 2 Диагонали параллелепипеда пересекаются и деляться точкой пересечения пополам.
3. Имеются три четверки равных и параллельных ребер параллелепипеда: 1 – АВ, А1В1, D1C1, DC, 2 – AD, A1D1, B1C1, BC, 3 – АА1, ВВ1, СС1, DD1.
3. Прямой параллелепипедОпределение. Параллелепипед называется прямым, если его боковые ребра перпендикулярны основаниям.
Пусть боковое ребро АА1 перпендикулярно основанию (рис. 3). Это означает, что прямая АА1 перпендикулярна прямым АD и АВ, которые лежат в плоскости основания. А, значит, в боковых гранях лежат прямоугольники. А в основаниях лежат произвольные параллелограммы. Обозначим, ∠BAD = φ, угол φ может быть любым.
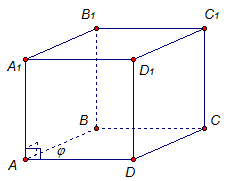
Рис. 3 Прямой параллелепипед
Итак, прямой параллелепипед - это параллелепипед, в котором боковые ребра перпендикулярны основаниям параллелепипеда.
4. Прямоугольный параллелепипедОпределение. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию. Основания являются прямоугольниками.
Параллелепипед АВСDА1В1С1D1 – прямоугольный (рис. 4), если:
1. АА1⊥ АВСD (боковое ребро перпендикулярно плоскости основания, то есть параллелепипед прямой).
2. ∠ВАD = 90°, т. е. в основании лежит прямоугольник.
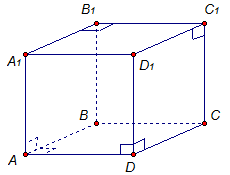
Рис. 4 Прямоугольный параллелепипед
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда. Но есть дополнительные свойства, которые выводятся из определения прямоугольного параллелепипеда.
Итак, прямоугольный параллелепипед - это параллелепипед, у которого боковые ребра перпендикулярны основанию. Основание прямоугольного параллелепипеда - прямоугольник.
5. Свойства прямоугольного параллелепипеда1. В прямоугольном параллелепипеде все шесть граней прямоугольники.
АВСD и А1В1С1D1 – прямоугольники по определению.
2. Боковые ребра перпендикулярны основанию. Значит, все боковые грани прямоугольного параллелепипеда - прямоугольники.
3. Все двугранные углы прямоугольного параллелепипеда прямые.
Рассмотрим, например, двугранный угол прямоугольного параллелепипеда с ребром АВ, т. е. двугранный угол между плоскостями АВВ1 и АВС.
АВ – ребро, точка А1 лежит в одной плоскости – в плоскости АВВ1, а точка D в другой – в плоскости А1В1С1D1. Тогда рассматриваемый двугранный угол можно еще обозначить следующим образом: ∠А1АВD.
Возьмем точку А на ребре АВ. АА1 – перпендикуляр к ребру АВ в плоскости АВВ1, AD перпендикуляр к ребру АВ в плоскости АВС. Значит, ∠А1АD – линейный угол данного двугранного угла. ∠А1АD = 90°, значит, двугранный угол при ребре АВ равен 90°.
∠(АВВ1, АВС) = ∠(АВ) = ∠А1АВD= ∠А1АD = 90°.
Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.
6. ТеоремаКвадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Примечание. Длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда, являются измерениями прямоугольного параллелепипеда. Их иногда называют длина, ширина, высота.
Дано: АВСDА1В1С1D1 – прямоугольный параллелепипед (рис. 5).
Доказать: 
.
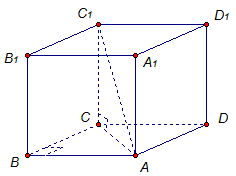
Рис. 5 Прямоугольный параллелепипед
Доказательство:
Прямая СС1 перпендикулярна плоскости АВС, а значит, и прямой АС. Значит, треугольник СС1А – прямоугольный. По теореме Пифагора:
Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора:
Но ВС и AD – противоположные стороны прямоугольника. Значит, ВС = AD. Тогда:
Так как , а , то
. Поскольку СС1 = АА1, то 
что и требовалось доказать.
Диагонали прямоугольного параллелепипеда равны.
Обозначим измерения параллелепипеда АВС как a, b, c (см. рис. 6), тогда АС1 = СА1 = В1D = DВ1 = 
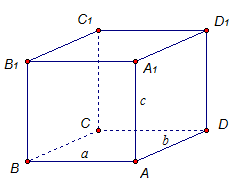
Рис. 6
8. КубОпределение. Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом.
Все грани куба – это равные квадраты.
9. Задача 1 Найти диагональ кубаНайти диагональ куба с ребром 1 (рис. 7).
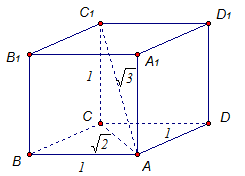
Рис. 7
Решение:
см.
Ответ: 
см.
Рисунок
Дан куб АВСDА1В1С1D1 (рис. 8). Докажите, что плоскости АВС1 и А1В1D перпендикулярны.
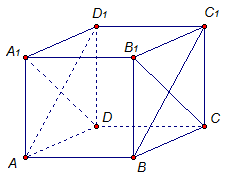
Рис. 8
Доказательство:
Прямые ВС1 и В1С перпендикулярны как диагонали квадрата ВВ1С1С.
Прямая DC перпендикулярна плоскости ВВ1С1, а значит, и прямой ВС1, которая лежит в этой плоскости.
Имеем, прямая ВС1 перпендикулярна двум пересекающимся прямым В1С и DC плоскости, значит А1В1D. Значит, прямая ВС1 перпендикулярна плоскости А1В1D.
Плоскость АВС1 проходит через перпендикуляр ВС1 ко второй плоскости А1В1D, значит, плоскости АВС1 и А1В1D перпендикулярны по признаку, что и требовалось доказать.
Конспект по теме: " Прямоуголный параллелепипед" (95.5 KB)
0
2202
110
Нравится
0
