Конспект открытого урока по теме "Длина окружности"

№ п/п

Этап урока

Методы, реализуемые на этапе

Действия учителя

Действия учащихся

УУД (с указанием вида: личностные, регулятивные, познавательные, коммуникативные)

1

2

3

4

5

6

1.

Оргмомент урока

Метод стимулирования отношений долга и ответственности

Актуализирует проявление учащимися установок на сотрудничество и успех в предстоящей работе.

Оценивает или вносит коррективы в готовность рабочих мест учащихся.

Выполняют необходимые действия.

Демонстрируют готовность к учебной деятельности

Оценивать ситуации взаимодействия в соответствии с правилами поведения и этики.

(коммуникативные)

Мотивация учебной деятельности

Метод стимулирования положительной самооценки перспектив включения в УД

Обращается к учащимся со словами:

У нас сегодня необычный урок. Сегодня мы с вами совершим необычную поездку, мы посетим загадочное царство- государство круга. В этой стране мы сделаем несколько остановок: побываем в деревне математических знаний, посетим мастерскую круга, сделаем привал на поляне отдыха, заглянем в космос. На каждой остановке вам надо будет показать свои знания, находчивость и смекалку. И поэтому итогом нашего путешествия будет получение новых знаний, умений и способностей.

(презентация слайд 1)

Слушают и

оценивают предложение

учителя,

определяют смысл

предстоящего поиска.

Осознание осваиваемого на уроке приема учебной деятельности, как ценности.

(личностные)

Целеполагание

Метод самоопределения в целях по аналогии с уже известным и усвоенным учащимися.

Помогает сформулировать цели предстоящей учебной деятельности по аналогии с целями изучения предыдущих приемов учебной работы, в частности приемов решения текстовых задач.

(презентация слайд 3)

Определяют, что предстоит:

• Запомнить (понятие длины окружности и формулы для ее нахождения) и

• Уметь (отличать радиус от диаметра, хорду от диаметра, длину окружности от площади круга; уметь применять формулы для решения задач).

Самоопределение в целях учебной деятельности

(регулятивные)

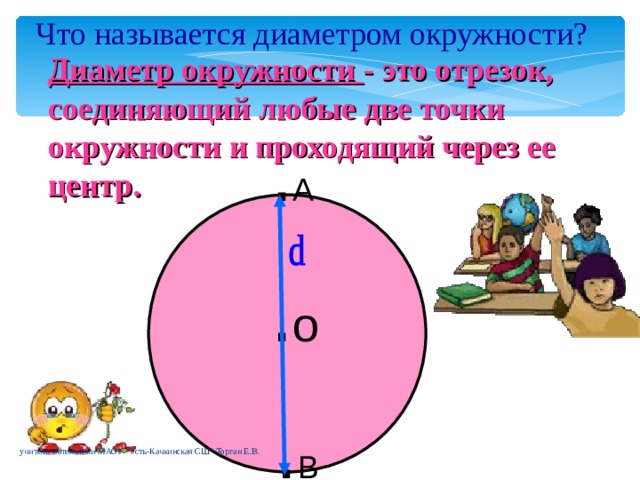
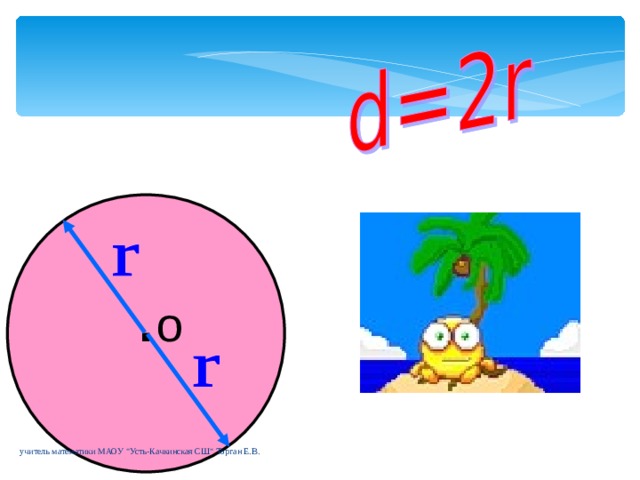
Повторение опорных знаний

(Выявление пробелов первичного осмысления изучаемого материала)

Беседа с учащимися

Предлагает вспомнить:

Понятие окружности, радиуса, диаметра, хорды.

( презентация слайды 4-7)

Актуализируют необходимые установки,

Сравнивают /…/,

Вспоминают /…/,

Аргументируют (объясняют) /…/.

Самооценка соответствия имеющихся знаний и умений заявленным требованиям

(регулятивные)

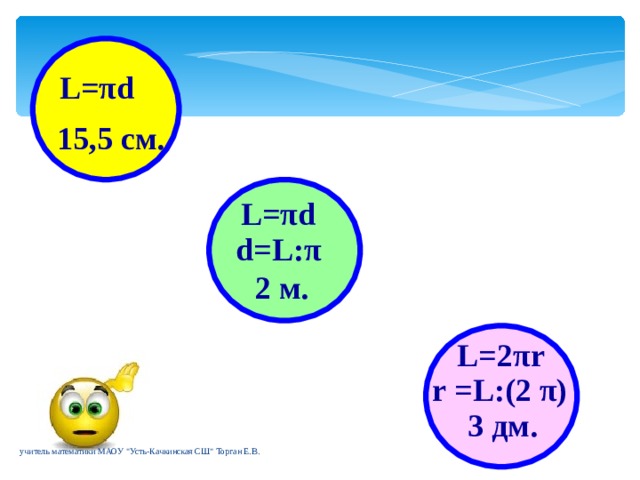
2.

Изучение нового материала

Проблемный метод

1. Создает проблемную ситуацию.

Учитель: - Нам предстоит решить задачу, «Какой длины надо взять кусок проволоки, чтобы согнуть окружность данного радиуса?».

(презентация слайды 8-10)

(презентация слайд 11)

(презентация слайды 12-14)

• Выдвигают гипотезы:

1. рассмотреть…;

2. обеспечить …;

3. использовать … и т.д.

• Проверяют, принимают или отвергают варианты решения

• Анализируют и дают решение проблемы

Планирование своей деятельности для решения поставленной задачи (регулятивные).

Анализ и синтез

объектов, структурирование знаний, подведение под понятие,

поиск и выделение необходимой информации на основе наблюдения и оценки выявленных закономерностей.

(познавательные).

Умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог (коммуникативные). Проявление терпения и проявление доброжелательности и доверия к собеседнику, смыслообразование (личностные)

Физминутка

Здоровьесбережение

Учитель меняет деятельность учащихся, обеспечивает эмоциональную разгрузку учащихся.

(Презентация слайд 15)

Учащиеся сменяют вид деятельности (подвижный отдых) и готовятся продолжать работу.

Осознание

необходимости в упражнениях для глаз (познавательные)

Саморегуляция (регулятивные)

Умение слушать (соблюдение тишины) (коммуникативные)

Осознание ценности здоровья

(личностные)

3.

Закрепление (обеспечение осознанности формируемых знаний и умений).

Самостоятельная работа с самопроверкой по эталону

Демонстрирует:

(Презентация слайд 16)

(Презентация слайды 17-19)

Даёт задание: Учитель: - Мы решили несколько задач, и вы можете уже сказать насколько хорошо или не очень вы усвоили формулы.
На презентации слайд 20 задачи разного уровня первая самая простая, вторая посложнее, третья ещё сложнее

- Прочтите задачи и выберете одну для самостоятельного решения. (презентация слайды 20-21)
- Выявляет возникающие затруднения, организует соответствующие рефлексивные действия учащихся.

Выполняют задания в тетрадях. При необходимости обращаются за помощью. Сравнивают полученный ответ с ответом на экране. Оценивают себя

Планирование своей деятельности для решения поставленной задачи,

саморегуляция,

самоконтроль в форме сравнения способа действия и его результата с заданным эталоном с целью обнаружения отклонений от эталона и внесение необходимых корректив.

(регулятивные)

4.

Итог урока

Самостоятельная работа с самопроверкой по эталону

Вносит корректировку в ответы учащихся. Дает возможность самим ученикам указать на листочках правильные, оценить себя, затем оценивает учащихся с комментированием.

Рефлексия.

(презентация слайда 22)

Даёт задание:

(презентация слайда 23)

№852, №851-задачи аналогичные тем, что мы решали сегодня на уроке.
Придумайте и составьте задачу по теме «Длина окружности» и сделайте красочный рисунок к задаче.

Рефлексия (презентация слайды 24-26)

Выполняют задания, сравнивают полученные результаты с вариантами возможных ответов, указывают правильные, оценивают себя.

Планирование своей деятельности для решения поставленной задачи,

саморегуляция,

самоконтроль в форме сравнения способа действия и его результата с заданным эталоном с целью обнаружения отклонений от эталона и внесение необходимых корректив.

(регулятивные)

Умение слушать и вступать в диалог

(коммуникативные)

Моральная ответственность перед собой, коллективом и учителем (личностные)

Порядковый номер,

№

Длина окружности,

С

Диаметр окружности,

d

Во сколько раз длина окружности больше диаметра, С/d

ВЫВОД

№

ВОПРОС

ОТВЕТ

1

Отрезок, соединяющий две точки окружности

А) хорда, Б) Диаметр В) радиус

2

Число π равно

А) 3, 15 Б)3,14 В)6,28

3

Формула длины окружности

А) С=πr Б) С=πd

В) C=2πd Г) C=2r

4

Чему равен диаметр окружности, радиус

которой 3,2 см?

А) 1,9 Б) 6,6

В) 7,6 Г) 6,4

5

Диаметр равен половине радиуса

А) да Б) нет

ОЦЕНКА

______