Министерство образования, науки и молодежной политики Краснодарского края
ГБПОУ КК «Колледж Ейский»
КОНСПЕКТ ЛЕКЦИЙ
по физике
для студентов 1-2 курсов специальностей технического профиля СПО
Раздел 2. Постоянный ток
Ейск, 2017
|
| |
Конспект лекций по физике состоит из трех разделов, в которых в доступной форме излагаются физические основы электродинамики, нацелен на систематизацию и конкретизацию знаний, приобретенных в процессе изучения учебной дисциплины Физика, и содержит материал, достаточный для успешного прохождения студентами текущей и промежуточной аттестации.
Конспект лекций подготовлен согласно тематике рабочей программы учебной дисциплины и включает широкий спектр вопросов для самоконтроля.
Разработчик: преподаватель ГБПОУ КК «Колледж Ейский» Л.С.Черных
СОДЕРЖАНИЕ
Тема 1. Законы постоянного тока
Лекция 1. Закон Ома 4
Лекция 2. Электродвижущая сила источника тока 9
Лекция 3. Закон Ома для полной цепи. Правила Кирхгофа 12
Лекция 4. Работа и мощность тока. Тепловое действие тока 16
Тема 2. Ток в металлах
Лекция 5. Классическая электронная теория проводимости
металлов 22
Лекция 6. Зонная теория 28
Тема 3. Ток в жидкостях
Лекция 7. Электролиз и электролитическая диссоциация 35
Тема 4. Ток в газах и вакууме
Лекция 8. Электропроводность газов. Электрический ток в
вакууме 41
Литература 55
Постоянный ток
Тема 1. Законы постоянного тока
Лекция № 1. Закон Ома.
Цель: выяснить природу электрического тока, условия его появления и существования, определить его количественные характеристики и законы.
Основные понятия:
Электрический ток – упорядоченное движение электрических зарядов.
Линии тока – линии, вдоль которых происходит упорядоченное движение зарядов.
Плотность тока – физическая величина, численно равная заряду, проходящему в единицу времени через единичное сечение проводника, перпендикулярное вектору скорости зарядов.
Сила тока – физическая величина, численно равная заряду, проходящему через сечение проводника в единицу времени.
Сопротивление проводника – физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношению напряжения на концах проводника к силе тока, протекающего по нему.
Удельное сопротивление проводника – сопротивление однородного цилиндрического проводника, имеющего единичную длину и единичную площадь поперечного сечения.
Удельная проводимость проводника – физическая величина, характеризующая способность проводника проводить электрический ток и обратная удельному сопротивлению.
1.1. Понятие об электрическом токе.
Упорядоченное движение электрических зарядов называется электрическим током. Ток, возникающий в проводнике вследствие того, что в нем создается электрическое поле, называется током проводимости. При движении зарядов нарушается их равновесное распределение: поверхность проводника уже не является эквипотенциальной и электрические силовые линии не направлены перпендикулярно ей, так как для движения зарядов необходимо, чтобы на поверхности проводника тангенциальная составляющая напряженности электрического поля не равнялась нулю (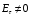 ). Но тогда и внутри проводника должно существовать электрическое поле, ибо, как известно из электростатики, внутри проводника нет поля лишь в случае равновесного распределения зарядов на поверхности этого проводника. Перемещение зарядов – электрический ток – продолжается до тех пор, пока все точки проводника не станут эквипотенциальными.
). Но тогда и внутри проводника должно существовать электрическое поле, ибо, как известно из электростатики, внутри проводника нет поля лишь в случае равновесного распределения зарядов на поверхности этого проводника. Перемещение зарядов – электрический ток – продолжается до тех пор, пока все точки проводника не станут эквипотенциальными.
Таким образом, для появления и существования тока проводимости необходимы два условия.
Первое – наличие в данной среде носителей заряда, т.е. заряженных частиц, которые могли бы в ней перемещаться.
Второе – наличие в данной среде электрического поля, энергия которого затрачивалась бы на перемещение электрических зарядов. Для того чтобы ток был длительным, энергия поля должна все время пополняться, иными словами, нужен источник электрической энергии – устройство, в котором осуществляется преобразование какого-либо вида энергии в энергию электрического поля.
В металлах могут свободно перемещаться только электроны. Поэтому электрический ток в металлах есть движение электронов проводимости. В проводящих растворах нет свободных электронов, а подвижными заряженными частицами являются ионы. В газах могут существовать в подвижном состоянии и ионы, и электроны. Направлением тока условились считать направление движения положительных частиц. Поэтому направление тока в металлах противоположно направлению движения электронов.
Линии, вдоль которых происходит упорядоченное движение зарядов, называют линиями тока. За их направление (по историческим причинам) принято считать направление движения положительных зарядов.
1.2. Сила и плотность тока.
Пусть концентрация свободных электронов в металле равна n, а заряд каждого носителя равен е. Выделим внутри проводника прямоугольник с сечением площадью dS, перпендикулярным вектору скорости упорядоченного движения зарядов 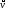 . Сечение характеризуется нормальным к нему вектором
. Сечение характеризуется нормальным к нему вектором 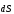 . Построим на этом сечении параллелепипед высотой, численно равной скорости
. Построим на этом сечении параллелепипед высотой, численно равной скорости 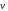 . За 1 с через выделенное сечение пройдут те и только те заряды, которые находятся внутри параллелепипеда. Они перенесут заряд
. За 1 с через выделенное сечение пройдут те и только те заряды, которые находятся внутри параллелепипеда. Они перенесут заряд 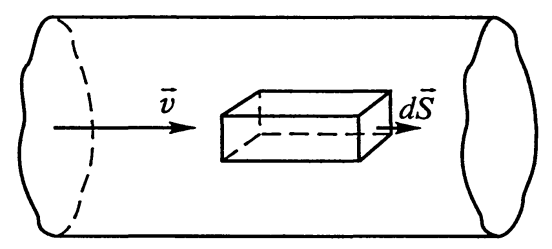
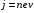 .
.
Если рассматривать 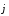 как вектор, то предыдущее выражение примет вид:
как вектор, то предыдущее выражение примет вид:
 .
.
Физическую величину 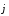 называют плотностью тока; она численно равна заряду, проходящему в 1 с через единичное сечение проводника, перпендикулярное вектору скорости зарядов. Заметим, что при изменении знака заряда меняется и знак скорости, так что знак вектора плотности тока не изменяется.
называют плотностью тока; она численно равна заряду, проходящему в 1 с через единичное сечение проводника, перпендикулярное вектору скорости зарядов. Заметим, что при изменении знака заряда меняется и знак скорости, так что знак вектора плотности тока не изменяется.
При постоянном токе вектор 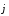 постоянен по всему выбранному сечению проводника. Поэтому, суммируя по сечению, получим:
постоянен по всему выбранному сечению проводника. Поэтому, суммируя по сечению, получим:
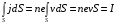 ,
,
где I – сила тока, численно равная полному заряду q, проходящему через сечение проводника в единицу времени.
При токе, меняющемся во времени, это определение заменяется более общим:
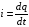 .
.
Сила тока - скалярная величина.
Основной единицей в СИ является единица силы тока – ампер (А). При силе тока 1 А через сечение проводника в 1 с проходит заряд, равный 1 Кл, следовательно,
1 Кл = 1 А с.
Единицей плотности тока является 1 А/м2.
Если скорость упорядоченного движения зарядов не меняется, то плотность тока и сила тока также остаются постоянными во времени. Такой ток называют постоянным (или стационарным). В этом случае последнее уравнение можно переписать в виде:
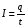 ,
,
где q и t – конечные (а не бесконечно малые) значения заряда и промежутка времени.
Еще раз подчеркнем, что сила тока – скалярная характеристика процесса. Распространенное выражение «направление тока» имеет смысл только по отношению к вектору плотности тока.
1.3. Закон Ома для однородного участка цепи.
При токе заряды движутся, так как внутри проводника существует электрическое поле, характеризуемое напряженностью 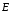 , которое вызывает и поддерживает упорядоченное движение зарядов. Поэтому между концами проводника с током существует разность потенциалов U (ее часто называют напряжением или падением напряжения на соответствующем участке). Сила тока является функцией этой разности потенциалов:
, которое вызывает и поддерживает упорядоченное движение зарядов. Поэтому между концами проводника с током существует разность потенциалов U (ее часто называют напряжением или падением напряжения на соответствующем участке). Сила тока является функцией этой разности потенциалов:
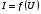 .
.
Вид этой функции обычно довольно сложен. Но есть простой частный случай, очень важный практически (токи в металлах и жидкостях), когда при данных внешних условиях (в частности, температуре) отношение разности потенциалов U к силе тока I оказывается постоянным, не зависящим от U:
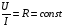 ,
,
т. е.
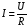 .
.
Это известный закон Ома для участка цепи.
Величина R называется сопротивлением проводника и выражается в омах (Ом):
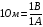 .
.
Как показывает опыт, в металлическом проводнике концентрация свободных электронов (электронов проводимости) не зависит от напряженности поля и, следовательно, от приложенного к проводнику напряжения. Кроме того, при постоянном токе в однородном проводнике плотность тока во всех участках поперечного сечения проводника одинакова – ток распределен по сечению равномерно.
1.4. Закон Ома в дифференциальной форме.
Применим закон Ома к однородному металлическому проводнику длиной l и сечением S, между концами которого создана разность потенциалов U, поддерживающая силу тока I. Вследствие симметричной формы провода электрическое поле в нем имеет напряженность, равную
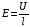 ,
,
а модуль плотности тока равен
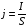 .
.
Подставляя эти выражения в формулу закона Ома, получим:
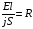 .
.
Откуда
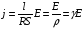 ,
,
где и – соответственно удельное сопротивление и удельная проводимость вещества проводника, причем 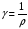 .
.
За положительное направление вектора плотности тока принимают направление скорости упорядоченного перемещения положительных зарядов, т. е. направление вектора напряженности, поэтому последнее выражение можно записать в векторной форме:
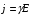 .
.
Это уравнение представляет собой закон Ома в дифференциальной форме, применимой в каждой точке внутри проводника.
Удельное сопротивление
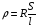
численно равно сопротивлению проводника, имеющего форму куба со стороной, равной 1 м. Единицей удельного сопротивления в СИ является Ом метр. Последнее соотношение верно для проводников цилиндрической формы (для других форм зависимость от геометрии будет другой). Из последнего соотношения следует, что
.
Вопросы для самоконтроля.
1. Что называется электрическим током и каковы условия возникновения тока проводимости?
2. Что называют плотностью тока? силой тока?
3. Сформулируйте закон Ома для однородного участка цепи.
4. Сформулируйте закон Ома в дифференциальной форме
5. Что называют удельным сопротивлением? удельной проводимостью проводника?
6. Как зависит сопротивление проводника от его длины, площади поперечного сечения и материала?
Лекция № 2. Электродвижущая сила источника тока.
Цель: ввести понятие «электродвижущая сила», определить его физический смысл.
Основные понятия:
Сторонние силы – силы неэлектростатического происхождения, действующие на свободные заряды и поддерживающие ток в цепи.
Электродвижущая сила (ЭДС) – работа, которую совершают сторонние силы при перемещении единичного положительного заряда вдоль всей цепи.
Если в проводнике создать электрическое поле и не принять мер для его поддержания, то перемещение носителей заряда приведет очень быстро к тому, что поле внутри проводника исчезнет и, следовательно, ток прекратится. Для того чтобы поддерживать ток достаточно длительное время, нужно от конца проводника с меньшим потенциалом (носители заряда предполагаются положительными) непрерывно отводить приносимые сюда током заряды, а к концу с большим потенциалом непрерывно их подводить (поддерживать постоянную разность потенциалов). Иными словами, необходимо осуществить круговорот зарядов, при котором они двигались бы по замкнутому пути. Но если бы во всех участках замкнутой электрической цепи плотность тока определялась бы только напряженностью электрического поля, то циркуляция этого поля по замкнутому контуру цепи оказалась отличной от нуля. Но, как известно, электростатическое поле есть поле потенциальное, циркуляция вектора напряженности которого тождественно равна нулю:
.
Поэтому в замкнутой цепи наряду с участками, на которых положительные заряды движутся в сторону убывания , должны иметься участки, на которых перенос положительных зарядов происходит в направлении возрастания , т. е. против сил электростатического поля (см. изображенную пунктиром часть цепи на рис.). Перемещение носителей на этих участках возможно лишь с помощью сил неэлектростатического происхождения, называемых сторонним силами. Таким образом, для поддержания тока необходимы сторонние силы, действующие либо на всем протяжении цепи, либо на отдельных ее участках. Они могут быть обусловлены химическими процессами, диффузией носителей заряда в неоднородной среде или через границу двух разнородных веществ, электрическими (но не электростатическими) полями, порождаемыми меняющимися во времени магнитными полями, и т. д. Для описания их действия на заряды вводится понятие напряженности сторонних сил. Напряженностью сторонних сил называется векторная физическая величина, равная отношению силы, действующей на положительный заряд, к этому заряду при неэлектростатическом взаимодействии.
Постулируется, что напряженность сторонних сил, так же как и напряженность электростатического поля, подчиняется принципу суперпозиции.
Следовательно, если на участке электрической цепи действуют, кроме электрических, сторонние силы, то результирующая напряженность будет определяться векторной суммой напряженности электрического поля 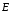 и напряженности сторонних сил
и напряженности сторонних сил . В этом случае закон Ома в дифференциальной форме примет вид:
.
Циркуляция результирующего вектора по замкнутому контуру электрической цепи равна циркуляции по контуру цепи вектора напряженности только сторонних сил, так как циркуляция вектора напряженности электрического поля равна нулю из-за его потенциальности:
.
Выражение для циркуляции напряженности сторонних сил по контуру цепи имеет простой физический смысл. Оно равно отношению работы, производимой сторонними силами по перемещению положительного заряда в замкнутой электрической цепи к этому заряду. Эта величина носит название электродвижущей силы (ЭДС) – E :
E .
Единицей ЭДС в СИ является вольт.
Силы неэлектростатической природы создаются специальными техническими устройствами, называемыми источниками ЭДС или источниками тока. Наличие в электрической цепи источника ЭДС является вторым необходимым условием существования постоянного тока в цепи. Источниками тока могут быть, например, гальванические элементы, где разность потенциалов между разнородными электродами, помещенными в раствор электролита, поддерживается за счет химических процессов, происходящих в элементе, индукционные генераторы, в которых разность потенциалов возникает на концах проводящей обмотки, вращающейся в магнитном поле, и др.
По результатам своего действия любой источник ЭДС представляет собой процесс или устройство, отделяющее положительные заряды от отрицательных. После разделения заряды перемещаются на электроды и по закону Кулона действуют на заряды проводника вблизи электродов, которые в свою очередь действуют на другие заряды, и т. д. В результате этих коллективных взаимодействий в цепи на поверхности проводников возникает такое распределение зарядов, которое обеспечивает существование внутри проводника соответствующего электрического поля. Таким образом, роль зарядов на полюсах источника сторонних ЭДС состоит не в том, чтобы создавать во всех проводниках непосредственно соответствующее электрическое поле, а в том, чтобы обеспечить такое распределение поверхностных зарядов на проводниках, которое создает нужное электрическое поле внутри них. А это и обеспечивает существование постоянного тока.
Источник ЭДС обладает некоторым внутренним сопротивлением, зависящим от его устройства; это сопротивление оказывается последовательно включенным в общую электрическую цепь. Поэтому при протекании тока разность потенциалов (падение напряжения) на зажимах источника тока оказывается меньше, чем ЭДС, на величину Ir, где I – сила тока, r – внутреннее сопротивление. В существовании внутреннего сопротивления у источника тока легко убедиться, подключив вольтметр к зажимам источника и уменьшая внешнее сопротивление цепи. Измеряемая вольтметром разность потенциалов U уменьшается при увеличении силы тока по закону:
U = E – Ir.
Источники ЭДС можно разбить на два различных класса:
1. При во внешней цепи существует практически неизменная разность потенциалов, равная ЭДС. Такие источники называют источниками напряжения, или ЭДС. Здесь сила тока обратно пропорциональна сопротивлению R.
2. При в цепи получается практически неизменный ток, а напряжение меняется пропорционально нагрузочному сопротивлению R. Такие источники называют источниками тока.
Вопросы для самоконтроля.
1. Почему электростатическое поле не способно поддерживать постоянный ток в цепи?
2. Какие силы называются сторонними?
3. Что называют электродвижущей силой? В чем ее измеряют?
4. Из чего складывается полное сопротивление цепи?
Лекция № 3. Закон Ома для полной цепи. Правила Кирхгофа.
Цель: обобщить закон Ома на случай замкнутой цепи и любого ее участка, изучить метод (правила Кирхгофа) расчета сложных цепей.
Основные понятия:
Напряжение (падение напряжения) – физическая величина, численно равная работе, совершаемой суммарным полем кулоновских и сторонних сил при перемещении единичного положительного заряда вдоль участка цепи из точки 1 в точку 2.
3.1. Закон Ома для участка цепи с ЭДС (неоднородного участка).
Закон Ома в том виде, как он приведен ранее, справедлив для однородной цепи, т. е. такой, в которой нет никаких ЭДС. Однако мы уже отмечали, что возникновение постоянного тока в цепи возможно лишь при наличии ЭДС. Рассмотрим участок электрической цепи постоянного тока между точками 1 и 2, содержащий резистор сопротивлением R и источник тока, имеющий ЭДС E и внутреннее сопротивление r.
Участок 1-2 представляет часть электрической цепи, в которой могут быть включены как другие источники тока, так и другие элементы цепи (резисторы, конденсаторы, лампы накаливания и др.).
В соответствии с законом Ома в дифференциальной форме плотность тока на участке 1-2 будет зависеть как от напряженности электрического поля, так и от напряженности сторонних сил на этом участке:
.
Умножим скалярно обе части этого выражения на вектор , модуль которого равен элементарной длине элемента проводника на участке 1-2, а направление совпадает с направлением вектора плотности тока на этом участке. После перемножения получим:
Левая часть данного соотношения может быть выражена через силу тока и сопротивление рассматриваемого участка цепи следующим образом:
,
где – удельное сопротивление рассматриваемого участка цепи, S – площадь его поперечного сечения. Так как по определению , то можно записать
.
Здесь произведение выражает элементарную работу электрического поля по перемещению единичного положительного заряда на участке
, произведение
определяет элементарную работу сторонних сил на этом же участке цепи.
Проинтегрируем последнее выражение на участке цепи между точками 1 и 2:
.
Так как участок 1-2 не имеет разветвлений, то левая часть выражения равна произведению силы тока I на сопротивление R12 этого участка:
.
Для однородного линейного проводника и
. Условие однородности выполняется, если
. В этом случае
.
Первое слагаемое в правой части представляет работу электрического поля на участке 1-2 по переносу единичного положительного заряда между точками 1 и 2, т. е.
.
Знаки для потенциалов следует выбирать, ориентируясь по направлению тока. Так как ток течет от точки с большим потенциалом к точке с меньшим потенциалом, то работа поля будет положительной при переходе от одной точки к другой по направлению тока. Направление тока в данном случае совпадает с направлением обхода от точки 1 к точке 2 вдоль dl, поэтому значение элементарной работы положительно, и потенциал 1 больше потенциала 2.
Второе слагаемое по определению есть ЭДС на рассматриваемом участке электрической цепи. Если источник ЭДС включен на участке 1-2 так, что сторонние силы способствуют протеканию тока, то ЭДС следует брать со знаком плюс, если сторонние силы препятствуют протеканию тока, то ЭДС следует брать со знаком минус.
С учетом сказанного проинтегрированное выражение перепишем в виде:
E12.
Таким образом, можно утверждать, что произведение силы тока на сопротивление участка цепи, содержащего ЭДС, равно алгебраической сумме разности потенциалов на концах участка и ЭДС, действующей на этом участке цепи. При этом ток считается положительным, если его направление совпадает с направлением обхода участка цепи, знак разности потенциалов определяется направлением тока, а знак ЭДС определяется в зависимости от полярности включения источника ЭДС в цепь: если ток проходит источник ЭДС от – к +, то ЭДС берется со знаком плюс, если от + к –, то со знаком минус.
Последнее соотношение выражает закон Ома для участка цепи, содержащего источник ЭДС. Участок цепи, содержащий источник ЭДС, называется неоднородным участком цепи.
Для участка цепи, содержащего источник ЭДС, вводят, также, понятие напряжения: напряжением на участке цепи 1-2 называется физическая величина U12, численно равная работе, совершаемой суммарным полем кулоновских и сторонних сил при перемещении вдоль цепи единичного положительного заряда из точки 1 в точку 2:
E12.
Введенное понятие напряжения не совпадает с тем, которым пользуются в электростатике для обозначения разности потенциалов, а является его обобщением. Напряжение на концах участка цепи равно разности потенциалов только в том случае, если на этом участке не приложены ЭДС.
3.2. Закон Ома для полной цепи. Если мы имеем неразветвленную замкнутую цепь, содержащую несколько резисторов сопротивлениями Ri и источников ЭДС Ek, обладающих внутренними сопротивлениями rk, то применяя к однородным участкам цепи закон Ома как для однородного участка цепи, а к неоднородному – закон Ома как для неоднородного участка цепи и складывая полученные выражения (с учетом того алгебраическая сумма всех потенциалов в замкнутой цепи обратится в нуль), получим выражение:
Eк.
Данное выражение называется законом Ома для полной (замкнутой) цепи постоянного тока: произведение силы тока на общее сопротивление всей цепи равняется алгебраической сумме всех ЭДС, приложенных в этой цепи.
При рассмотрении цепей постоянного тока нужно помнить, что направление тока в отдельных участках цепи может не совпадать с полярностью ЭДС, действующей на этом же участке.
Пусть замкнутая цепь состоит из источника электрической энергии с ЭДС E и внутренним сопротивлением r, а также внешней части цепи, имеющей сопротивление R. Силу тока в цепи найдем по закону Ома для полной цепи:
I = E /(R + r).
Разность потенциалов на электродах источника равна напряжению на внешней части цепи:
E – Ir
Если с помощью ключа К цепь разомкнуть, то ток в ней прекратится и, как видно из последней формулы, разность потенциалов на клеммах источника будет равна его ЭДС.
3.3. Правила Кирхгофа.
Расчет разветвленных цепей, особенно если в них имеются активные участки, сложен (во многих случаях его цель – нахождение токов по заданным сопротивлениям и ЭДС). Практически он сводится к рассмотрению отдельных участков цепи. Пусть, например, имеется цепь, схема которой показана на рисунке.
В узловых точках, где сходится несколько проводов, должен выполняться закон сохранения заряда: сумма притекающих токов, которым можно приписать положительный знак, должна равняться сумме вытекающих токов (с отрицательным знаком). Иначе говоря, для узлов алгебраическая сумма сил токов равна нулю:
.
Данное выражение называется первым правилом Кирхгофа и является следствием закона сохранения заряда, согласно которому ни в одной точке проводника не должны накапливаться или исчезать заряды.
Если выделить в цепи замкнутый контур (произвольный) и мысленно обойти его в некотором направлении (скажем, против хода стрелки часов), то сумма неизвестных разностей потенциалов обратится в нуль и получится:
Eк=
,
т. е. алгебраическая сумма ЭДС равна алгебраической сумме падений напряжения (с учетом падений напряжения на внутренних сопротивлениях источников). Правило знаков для E и IR такое же, как и выше. Данное выражение называется вторым правилом Кирхгофа и является обобщением закона Ома. Отличие от закона Ома состоит в том, что здесь токи в разных участках контура могут быть различными.
Написав число уравнений, равное числу неизвестных, можно решить их и получить данные о всех токах и напряжениях. Следует иметь в виду, что иногда написанные уравнения могут оказаться зависимыми и решение результата не даст. Умение выбрать надлежащие уравнения дается практикой.
Так, для узловых точек рассмотренной выше цепи получится:
.
Для верхнего параллельного контура найдем:
E1.
Для нижнего параллельного контура имеем:
E3,
где r1 и r3 – внутренние сопротивления источников ЭДС E1 и E3. Иногда бывает не ясно, какой знак следует приписать силе тока (т. е. как направлен вектор плотности тока). В этих случаях знак выбирают произвольно; о правильности выбоpa знака судят по окончательному знаку, получающемуся в результате вычислений: если сила тока оказывается положительной, то ее знак был выбран правильно; если отрицательной, то знак силы тока следует переменить на обратный.
Вопросы для самоконтроля.
1. Сформулируйте закон Ома для участка цепи с ЭДС.
2. Поясните физический смысл электродвижущей силы, напряжения и разности потенциалов.
3. В чем состоит закон Ома для полной цепи? Каков его физический смысл?
4. В чем состоят и на чем основаны правила Кирхгофа?
Лекция № 4. Работа и мощность тока. Тепловое действие тока.
Цель: ввести понятия «работа тока» и «мощность тока»; рассмотреть преобразование электрической энергии в тепловую, ее законы и применение.
Основные понятия:
Работа тока – работа, совершаемая электрическим полем на определенном участке электрической цепи.
Мощность тока – работа тока за единицу времени.
4.1. Работа и мощность тока.
При постоянной силе тока I через каждое сечение проводника за время dt переносится электрический заряд dq = Idt. Рассмотрим два сечения 1 и 2 в цепи постоянного тока. За время dt через первое сечение в объем проводника между сечениями 1 и 2 войдет заряд dq, и за это же время через второе сечение из этого объема выйдет такой же заряд dq, что эквивалентно непосредственному переносу заряда dq между сечениями 1 и 2 за время dt. При этом электрическое поле на участке 1-2 совершает работу dA, равную произведению dq на разность потенциалов между этими сечениями:
,
здесь через U обозначена разность потенциалов .
Работа, совершаемая электрическим полем на определенном участке электрической цепи, называется работой тока.
Физическую величину, равную отношению работы тока dA ко времени ее совершения dt, называют мощностью тока. Мощность тока будем обозначать буквой Р. По определению:
.
Единицей мощности в СИ служит ватт (Вт).
4.2. Закон Джоуля-Ленца для однородного участка цепи.
Рассмотрим преобразование энергии на отдельном участке электрической цепи. Если участок не содержит ЭДС, то для него выполняется закон Ома. Умножив последний на Idt, получим
.
Правая часть представляет работу тока на рассматриваемом участке проводника. Согласно закону сохранения энергии эта работа расходуется на изменение внутренней энергии (нагревание) проводника и выделение некоторого количества теплоты в окружающую среду (при условии, что проводник неподвижен и в нем не происходит химических реакций). Так происходит до тех пор, пока проводник не нагреется до некоторой температуры Т, при которой заканчивается его нагревание (внутренняя энергия перестает изменяться) и вся работа тока затрачивается на выделение теплоты dQ в окружающую среду, т.е.
или
или
.
Т. о., количество теплоты, выделяемое в проводнике при протекании в нем постоянного тока, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока. Этот закон носит название закона Джоуля-Ленца. Механизм этого выделения достаточно прост: носители тока в результате работы сил поля приобретают дополнительную кинетическую энергию и затем расходуют ее на возбуждение колебаний решетки при столкновении с ее узлами-атомами.
Зависимость количества теплоты, выделяющейся в проводнике при прохождении тока, от сопротивления проводника можно продемонстрировать на следующих опытах. Возьмем два куска медной и нихромовой проволоки, одинаковых по длине и площади поперечного сечения. Удельное сопротивление нихрома приблизительно в 60 раз больше удельного сопротивления меди. Во столько же раз сопротивление куска R1 нихромового провода больше сопротивления R2 медного провода. Соединим эти провода последовательно и включим их в цепь аккумуляторной батареи Б через резистор (рис. а). Подбирая величину R его сопротивления, можно добиться того, что нихромовый провод раскалится докрасна. Температура медного провода при этом повысится незначительно, и до него можно дотронуться рукой. Этот опыт легко объяснить с помощью первой формулы . Сила тока в последовательно соединенных проводах одинакова. Поэтому выделяющиеся в них количества теплоты пропорциональны их сопротивлениям:
.
Соединим теперь медный и нихромовый провода параллельно и вновь включим в цепь аккумуляторной батареи (рис. б). В этом случае картина изменяется: медный провод раскаляется докрасна, а нихромовый почти не нагревается. Для объяснения этого опыта удобно воспользоваться формулой . Напряжения на параллельно соединенных проводах одинаковы. Поэтому выделяющиеся в проводах количества теплоты обратно пропорциональны их сопротивлениям:
.
4.3. Закон Джоуля-Ленца для неоднородного участка цепи и полной цепи.
Рассмотрим закон Джоуля-Ленца для неоднородного участка цепи. Если участок цепи содержит источник ЭДС, то для него справедлив закон Ома для неоднородного участка цепи. Умножая левую и правую части последнего на Idt, получим:
I E dt.
Из данного выражения видно, что количество теплоты, выделяющееся на неоднородном участке цепи, определяется алгебраической суммой работ тока и сторонних сил на этом участке. Отсюда видно, что протекание тока в таком участке сопровождается не только выделением теплоты, но и другими процессами, связанными с превращением энергии.
Для расчета количества теплоты в замкнутой цепи используем закон Ома для полной цепи. Умножив левую и правую части последнего на Idt, получим:
Eк.
Левая часть данного равенства представляет собой энергию, выделившуюся в цепи за время dt в соответствии с законом Джоуля-Ленца. Правая часть определяет работу по перемещению заряда в замкнутой электрической цепи, совершенную источником ЭДС. Анализируя данное равенство, еще раз убеждаемся в том, что ЭДС численно равна работе перемещения по замкнутой цепи единичного положительного заряда, совершаемой сторонними силами.
4.4. Тепловое действие тока.
Технические применения теплового действия тока многообразны: лампы накаливания, электропечи и различные бытовые нагревательные приборы, дуговая и контактная электросварка, электронные лампы, измерительная техника и т. п.
Чтобы сосредоточить выделение мощности тока в нужном участке цепи, необходимо цепь тока составить так, чтобы сопротивление того участка, где должно быть сосредоточено тепловое действие тока, значительно превышало сопротивление всех остальных участков цепи. Действительно, когда проводники включены в цепь последовательно, то ток I в них одинаков и количество тепла, выделяемого в каждом проводнике ежесекундно, прямо пропорционально сопротивлению проводника. Поэтому нить лампочки накаливания, имеющая большое сопротивление, раскаляется, тогда как медные провода, ведущие к ней ток, остаются холодными. То же можно сказать о нагревательных приборах. По той же причине место плохого соединения двух проволок (плохой контакт) электрической сети сильно нагревается током (для предотвращения этого в электрических установках концы соединяемых проволок тщательно спаивают).
Сосредоточение отдаваемой мощности (при последовательном соединении проводников) в проводнике, имеющем большое сопротивление, используется, в частности, при распылении металлов током. В этом случае ток подводят по массивным проводникам к тонкой проволочке и почти вся мощность тока идет на нагревание этой тонкой проволочки. Если взять батарею конденсаторов большой емкости, зарядить ее до разности потенциалов в десятки тысяч вольт и затем через массивные проводники и тонкую серебряную или другую проволоку разрядить эту батарею конденсаторов, то получается столь интенсивный разогрев проволоки, что она, не успев расплавиться, распыляется со вспышкой ослепительного белого света. В таких опытах была достигнута температура порядка 20 000 C, т. е. в три раза более высокая, чем температура поверхности Солнца. Распыление проволок током применяют для покрытия поверхностей тонким слоем металла – для металлизации поверхностей.
При параллельном соединении токи в проводниках будут разные, зато все они имеют общее напряжение; количества тепла, выделяемого ежесекундно, в этом случае обратно пропорциональны сопротивлениям, т. е. явление как раз противоположно тому, что наблюдается при последовательном соединении проводников. Поэтому если лампочки накаливания включены в цепь параллельно, как это и делается обыкновенно, то лампочка с меньшим сопротивлением будет брать на себя больше энергии, чем лампочка с большим сопротивлением.
Вопросы для самоконтроля.
1. Что называется работой тока?
2. Что называется мощностью тока? В чем она измеряется?
3. Сформулируйте закон Джоуля-Ленца для однородного участка цепи.
4. В чем состоит закон Джоуля-Ленца для неоднородного участка цепи
5. Приведите примеры технического применения теплового действия тока.
Тема 2. Ток в металлах
Лекция № 5. Классическая электронная теория проводимости металлов.
Цель: ознакомиться с классической электронной теорией проводимости металлов, вывести на ее основе законы постоянного тока, рассмотреть ее достоинства и недостатки.
Основные понятия:
Электронный газ – модель, описывающая поведение свободных электронов в металле.
Дрейф – упорядоченное движение электронов при создании в металле электрического поля.
5.1. Свободные электроны в металлах.
Какого рода свободные заряды находятся в металлических проводниках и связаны ли эти заряды с атомами металла? Для ответа на этот вопрос и выяснения природы носителей электрического тока в металлах был поставлен целый ряд специальных опытов.
В опытах Рикке (1901 г.) цилиндры из различных металлов с тщательно пришлифованными основаниями были прижаты друг к другу и через них целый год пропускался электрический ток. По окончании опыта цилиндры были разобраны и проанализированы на взаимное проникновение металлов. При этом были обнаружены лишь следы взаимного проникновения, не превышающие результатов обычной диффузии атомов в твердых телах.
Таким образом, оказалось, что перенос электрического заряда в металлах не связан с переносом самого вещества металла. Носители электрического тока не связаны с атомами и одинаковы во всех металлах. В металлический проводник, по которому идет постоянный ток, с одного конца входит такое же количество этих носителей тока, какое выходит с другого его конца, и заряд проводника при этом не изменяется.
Наличие в металле свободно перемещающихся зарядов должно проявляться в ряде инерционных эффектов. Если трамвай резко затормозить, то находящиеся внутри пассажиры будут двигаться по инерции вперед и скопятся у передней площадки вагона. Аналогично, если резко затормозить движущийся кусок металла, то находящиеся в нем свободные заряды, двигаясь по инерции, будут скапливаться у переднего конца его и между концами проводника возникнет определенная разность потенциалов. Так можно определить знак этих зарядов и их относительную подвижность.
Существование подобных электроинерционных эффектов было установлено в 1913 г. Л. И. Мандельштамом и Н. Д. Папалекси.
Количественные измерения относительной инертности носителей электрического тока в материалах были произведены в 1916 г. Стюартом и Толмэном. Из их опытов был определен удельный заряд e/m носителей электрического тока в металлах. Первые измерения дали
.
Незадолго до этого Милликен определил элементарный электрический заряд, который оказался равным е =1,6-10-19 Кл. Отсюда можно было оценить, что масса носителей тока в металлах m =10-30 кг и примерно в 2000 раз меньше массы самого легкого атома – атома водорода. Полученные значения удельного заряда и массы практически совпали с соответствующими значениями, измеренными ранее для электронов, движущихся в вакууме.
Таким образом, было окончательно установлено, что носителями электрического тока в металлах являются свободные электроны.
5.2. Законы Ома и Джоуля-Ленца в классической электронной теории.
Целый ряд фактов и косвенных данных привел физиков к выводу о наличии в металлах свободных электронов еще к началу XX века, задолго до того, как это было доказано прямыми опытами Стюарта и Толмэна. Перенеся на металлы некоторые представления и выводы кинетической теории газов, Лоренц и Друде разработали стройную теорию металлов, объяснявшую и связывавшую целый ряд свойств последних.
Вследствие сильного взаимодействия между атомами металла при соединении последних в кристаллическое твердое тело, самые внешние их электроны перестают быть связанными с отдельными атомами и легко переходят от одного атома к соседнему и далее через всю кристаллическую решетку. В узлах кристаллической решетки располагаются положительные ионы металла, а между ними хаотически движутся свободные электроны, образуя своеобразный электронный газ.
Считая, что каждый атом одновалентного металла отдает по одному электрону, а двухвалентного – по два, можно определить концентрацию свободных электронов в металлах. По порядку величины она оказывается равной 1028 - 1029 электрон/м3.
При столь большой концентрации электронов их взаимодействие между собой, как и с ионами кристаллической решетки металла, весьма велико. Однако, поскольку средняя сила, действующая на электрон со стороны всех остальных электронов и ионов, равна нулю, можно в первом приближении считать каждый электрон свободным, а его взаимодействие с ионами решетки и прочими электронами рассматривать как ряд последовательных соударений. Системе электронов в этом приближении приписывается лишь кинетическая энергия.
Именно этими чертами отличается идеальный газ. Поэтому Лоренц и Друде попытались построить теорию металлов, исходя из представления о том, что «электронный газ» в металлах есть идеальный газ, подчиняющийся законам статистики Максвелла-Больцмана.
В результате взаимодействия электронов и ионов кристаллической решетки, обусловленного их столкновениями, обе системы частиц должны приобрести одну и ту же температуру Т. Следовательно, средняя энергия хаотического движения электронов должна равняться
.
При комнатных температурах средняя скорость беспорядочного движения составляет u ~ 105 м/с.
При создании в металле электрического поля возникает упорядоченное движение (дрейф) электронов, т.е. электрический ток. Суммарная скорость заряда складывается из хаотической скорости и дрейфовой скорости. Но, т. к. хаотическая скорость направлена то по полю, то против поля, поэтому среднее значение последней равно нулю и, следовательно, суммарная скорость в среднем направлена по полю и равна средней скорости дрейфа v.
Рассмотрим отрезок проводника с поперечным сечением S. Направим вектор напряженности электрического поля 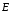 вдоль проводника. Каждый из свободных зарядов е внутри проводника приобретает направленную скорость
вдоль проводника. Каждый из свободных зарядов е внутри проводника приобретает направленную скорость 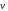 по полю. За промежуток времени dt через площадку S пройдут все те заряды, которые находятся на расстоянии от площадки S, не превышающем величину vdt, т. е. все заряды, заключенные в объеме цилиндра Svdt. Если число свободных зарядов в единице объема обозначить через n, то заряд dq, который пройдет за это время через поперечное сечение проводника в направлении электрического поля, будет
по полю. За промежуток времени dt через площадку S пройдут все те заряды, которые находятся на расстоянии от площадки S, не превышающем величину vdt, т. е. все заряды, заключенные в объеме цилиндра Svdt. Если число свободных зарядов в единице объема обозначить через n, то заряд dq, который пройдет за это время через поперечное сечение проводника в направлении электрического поля, будет
.
Отсюда величина тока, текущего в проводнике, равна
,
а плотность тока
.
Учитывая векторный характер скорости и плотности тока, можно последнюю формулу переписать в виде
.
Из последних формул, при большой плотности тока, например для меди, можно получить, что v ~ 10-5 м/с.
Следовательно, даже при значительных токах vu, и наличие электрического тока не сказывается на кинетических соотношениях, записанных выше и
,
где l – длина свободного пробега электрона.
Электрон под действием электрических сил поля
,
приобретает направленное движение с некоторым постоянным ускорением
.
Если среднее время свободного пробега есть , то электрон приобретает среднюю скорость дрейфа:
.
Однако электрон не может беспрепятственно продвигаться сквозь кристаллическую решетку. «Сталкиваясь» непрестанно с ионами, электрон отдает им кинетическую энергию своего направленного движения и вновь приобретает ее за счет энергии источника. Этот процесс повторяется снова и снова: в промежутках между ионами электрон разгоняется полем, затем, «сталкиваясь» с ионами, теряет скорость своего направленного движения, вновь разгоняется и т. д.
Таким образом, течение электрического тока, если его рассматривать в микрообъемах и за очень малые промежутки времени, представляется нам скачкообразным. Однако на расстояниях, неизмеримо больших, чем постоянная решетки, и за отрезки времени, неизмеримо большие, чем время свободного пробега электронов, перемещение электронов вдоль проводника можно считать равномерным, происходящим так же, как и движение тела под действием постоянной силы, равной силе трения. Только вместо трения здесь имеет место механизм непрестанных «столкновений» электронов с ионами.
Для плотности тока получается:
,
а это есть закон Ома, так как = const, если не зависит от напряженности поля 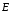 . Поскольку скорость дрейфа v много меньше средней скорости беспорядочного движения u, то это условие выполняется.
. Поскольку скорость дрейфа v много меньше средней скорости беспорядочного движения u, то это условие выполняется.
Из последнего уравнения следует, что электрическая проводимость не зависит от знака заряда, как это и должно быть.
Так как время свободного пробега уменьшается при росте u, то проводимость при этом должна уменьшаться, что отвечает действительности.
При движении электрона в течение времени со скоростью поле совершает над ним работу, равную
.
При концентрации электронов n над ними совершается работа
.
Но так как скорости распределены по направлениям совершенно беспорядочно, то второе слагаемое обращается в нуль.
За 1 с происходит соударений каждого электрона с решеткой металла. Поэтому в единице объема выделяется мощность
.
Таким образом, мы пришли к закону Джоуля-Ленца в дифференциальной форме.
5.3. Связь между электропроводностью и теплопроводностью металлов.
К этим успехам классической теории можно добавить еще получаемый из нее вывод о пропорциональности между электрической проводимостью и теплопроводностью (закон, ранее установленный экспериментально Видеманном и Францем). Было получено, что отношение коэффициента теплопроводности K к удельной проводимости равняется
,
где k – постоянная Больцмана. Положив , получим закон Видемана- Франца: отношение теплопроводности, к электропроводности для всех металлов должно быть одинаково и должно расти прямо пропорционально абсолютной температуре
.
Теоретическое значение константы закона Видемана–Франца a удовлетворительно согласовалось с экспериментальными значениями.
5.4. Недостатки классической электронной теории проводимости металлов.
Однако, несмотря на успехи классической электронной теории проводимости металлов Друде–Лоренца, она не смогла объяснить целого ряда явлений, наблюдающихся на опыте.
а) Экспериментально установлено, что в довольно большом интервале температур удельное сопротивление пропорционально абсолютной температуре (). Теория же Друде–Лоренца давала, что
.
Таким образом, классическая электронная теория не объяснила температурной зависимости удельного сопротивления металлов.
б) Возникли и трудности при оценке средней длины свободного пробега электронов в металле. Для того чтобы из теории Друде–Лоренца получить такие значения удельной электрической проводимости металла, которые не расходились бы с опытными данными, приходится принимать среднюю длину свободного пробега электронов в сотни раз большей, чем период решетки металла. Иными словами, приходится предположить, что электрон проходит без соударений с ионами решетки сотни межузельных расстояний. Такое предположение непонятно в рамках классической электронной теории Друде–Лоренца.
в) Еще большие затруднения возникли при подсчете теплоемкости металлов. Молярная теплоемкость металла должна складываться из теплоемкости ионной кристаллической решетки и теплоемкости электронного газа. Однако вычисленная таким образом теплоемкость превышала найденную из опытов Дюлонга и Пти теплоемкость в полтора раза. Если же при расчетах не учитывать теплоемкость электронного газа, то получается удовлетворительное согласие с опытными данными. Но такое пренебрежение теплоемкостью электронного газа абсолютно непонятно в рамках классической теории электропроводности, согласно которой, электронный газ ввиду своей высокой концентрации должен обладать большой величиной теплоемкости.
Вопросы для самоконтроля:
1. Какой вывод следовал из результатов опыта Рикке?
2. Какие выводы следовали из опытов Стюарта и Толмэна?
3. Какие гипотезы положены в основу классической электронной теории проводимости металлов?
4. Объясните на основании электронной теории закон Ома и закон Джоуля–Ленца.
5. Какова связь теплопроводности и электропроводности в металлах?
6. В чем состоят недостатки классической электронной теории проводимости металлов?
Лекция № 6. Зонная теория.
Цель: ознакомиться с основами зонной теории твердых тел.
Основные понятия:
Квантовая (волновая) механика – механика, описывающая законы движения микрочастиц с учетом их двойственной (корпускулярно-волновой) природы.
Спин – собственный момент количества движения частицы. Имеет квантовую природу и не связан с какими-либо перемещениями частицы.
Принцип Паули – один из фундаментальных принципов квантовой механики, согласно которому две частицы с полуцелым спином не могут одновременно находиться в одном состоянии.
Уровни энергии – возможные значения энергии квантовых систем (микрочастиц).
Энергетическая зона – система близких друг к другу дискретных уровней энергии.
6.1. Основы зонной теории твердых тел.
Рассмотренные выше противоречия указывают на то, что классическая электронная теория, представлявшая электрон как материальную точку, подчинявшуюся законам классической механики, не учитывала некоторых специфических свойств самого электрона, которые еще не были известны к началу XX века. Эти свойства были установлены позднее при изучении строения атома, и в 1924 г. была создана новая, так называемая квантовая или волновая механика движения электронов.
Коротко остановимся на современных представлениях о строении атома.
Атом состоит из ядра, вокруг которого движутся электроны. Орбиты электронов не произвольны, а строго определенны. На каждой орбите может одновременно находиться не более двух электронов. Однако и эти электроны не тождественны в своих свойствах. Установлено, что электроны обладают собственным, т. е. внутренне им присущим, моментом количества движения – спином (от английского слова «spin»—«веретено»). Электроны, движущиеся по одной орбите, должны отличаться направлением спина, т. е. также находятся в различных состояниях.
Таким образом, электроны, образующие электронную оболочку атома, подчиняются следующему закону: никакие два электрона не могут находиться в одном и том же состоянии. Этот закон, получивший название принципа Паули, оказался совершенно универсальным и применимым не только к электронам в атомах, но и к любым системам электронов.
Построим график энергий электронов для разных орбит какого-либо сложного атома. Наличие на данной орбите электрона— одного или двух — будем отмечать условно точками (острие стрелки спина, направленной на нас) и крестиками (оперение стрелки, направленной от нас) как это показано на рисунке.
Самым важным для дальнейшего является то обстоятельство, что качественно график уровней энергии системы электронов твердого тела имеет такой же вид. Согласно принципу Паули состояния электронов в любой системе должны различаться (двух электронов в одном и том же состоянии быть не может), а различным состояниям будут отвечать, вообще говоря, хоть сколько-нибудь различные энергии.
При образовании твердого тела из отдельных атомов и молекул происходит следующее. Состояния электронов, движущихся вокруг отдельных ядер на внутренних электронных оболочках, практически не меняются. Что же касается внешних электронных оболочек, то они в результате сближения отдельных атомов и возникающего при этом сильного взаимодействия между электронами перестраиваются. В одних случаях электроны продолжают удерживаться молекулами или ионами, которым они принадлежали. В этом случае подвижность электронов ограничена, и вещество представляет собой твердый диэлектрик, не способный проводить электрический ток, а лишь поляризующийся в электрическом поле. В других случаях электроны (валентные), как уже отмечалось выше, освобождаются, приобретают подвижность в веществе. В этом случае последнее представляет собой проводник – металл.
Особенно простую и наглядную картину электрических свойств твердых тел можно получить с помощью графиков энергии электронов в твердом теле, подобных графику энергий электронов в атоме.
Как и в случае отдельных атомов, значения энергии электронов в твердом теле образуют системы полос, в которых возможные значения энергии составляют множество очень близко расположенных уровней энергии (такие полосы называют разрешенными зонами), прерываемых полосами, в которых возможные для электронов значения энергии отсутствуют (такие полосы называют запрещенными зонами). Энергия, отвечающая переходу электрона с одного уровня на другой, соседний, внутри полосы совершенно ничтожна, во всяком случае много меньше средней кинетической энергии атомов кТ при комнатной температуре. Поэтому изменение состояния электрона внутри такой полосы можно было бы считать непрерывным, если бы не важное, отмеченное уже выше, обстоятельство – принцип Паули. Число различных состояний в случае их непрерывного изменения бесконечно велико. При ступенчатом же изменении состояний, т. е. при дискретной их последовательности, число состояний в каждой полосе конечно, а, следовательно, в соответствии с принципом Паули и число электронов, способных находиться в этих состояниях, также конечно.
Рассмотрим случай, когда нижние разрешенные зоны полностью укомплектованы электронами, ширина запрещенной зоны значительна (кТ), а над нею расположена зона, в которой электронов нет. Вещество, описываемое таким распределением электронов, есть диэлектрик. Действительно, состояние системы электронов может измениться только в том случае, если часть из них перейдет из нижних разрешенных энергетических зон в верхнюю разрешенную, но не занятую электронами зону. Но для этого нужна большая энергия, превышающая энергию теплового движения (кТ) или энергию, которую электрон может приобрести во внешнем поле. Следовательно, состояния электронов, ограниченные сверху широкой запрещенной зоной, меняться не могут. В частности, электроны не могут приобрести под влиянием слабого внешнего поля добавочную скорость (энергию), отвечающую возникновению тока проводимости.
Рассмотрим теперь случай, когда в верхней занятой зоне остаются незанятые энергетические уровни. Как мы увидим сейчас, этот случай отвечает металлам. Будем называть верхнюю, свободную от электронов часть разрешенной зоны зоной проводимости. Переход электронов на уровни этой части разрешенной зоны связан с приобретением ими добавочной энергии (скорости), обусловливающей прохождение электрического тока. Начнем рассмотрение со случая, когда вещество обладает температурой, равной абсолютному нулю. Соответствующее этому случаю распределение электронов показано на рисунке а: все нижние энергетические уровни заняты парами электронов с противоположными спинами. При T=0°К энергия всей системы, в том числе и электронов, должна быть наименьшей из всех возможных. Хотя электроны, расположенные на верхних уровнях, и обладают сравнительно большой энергией, но перейти в состояние с меньшей энергией они не могут: ведь эти состояния уже заняты другими электронами. А появление двух или нескольких электронов в одном и том же состоянии невозможно (принцип Паули). Энергию электронов, занимающих самый высокий энергетический уровень (при T=0°К), мы будем обозначать . Ее величина по порядку равна 10-11 эрг (1 эрг = 10-7 Дж). Такого же порядка величины и средняя кинетическая энергия электронов при абсолютном нуле температуры. Для сравнения отметим, что средняя кинетическая энергия молекул одноатомного газа при комнатной температуре (T=300°К) составляет всего лишь 10-14 эрг. Следует твердо помнить, что огромная кинетическая энергия электронного газа в металлах обусловлена принципом Паули и имеет нетепловое происхождение. Ее нельзя отнять за счет понижения температуры: ведь движение электронов в атомах также не прекращается при приближении вещества к T=0°К. Следовательно, рассмотренный нами электронный газ в металлах при абсолютном нуле дает нам еще один пример того, что материя без движения немыслима. Абсолютный нуль для любых систем (диэлектриков, металлов и т. д.) означает не полное отсутствие движения, но состояние с минимальной возможной энергией, которую уже нельзя уменьшить за счет охлаждения. С повышением температуры колеблющиеся ионы решетки начинают передавать электронам энергию и переводить часть электронов на более высокие энергетические уровни. Однако даже при комнатных температурах средняя энергия теплового движения ~kT мала по сравнению со средней энергией электронов при абсолютном нуле
, и эта порция энергии достаточна лишь для перевода электрона на один из ближайших энергетических уровней. Рассматривая электроны, движущиеся на низших уровнях, мы видим, что все ближайшие более высокие уровни полностью заняты электронными парами. Нижний электрон мог бы перейти на более высокий энергетический уровень, лишь перепрыгнув все вышележащие, которые заняты. Но для такого большого энергетического скачка энергии порядка kT недостаточно. Поэтому поглощать тепловую энергию могут лишь электроны, находящиеся на наиболее высоких уровнях, как это показано на рисунке б, а таких электронов в металле сравнительно мало. Т. о., подавляющая часть электронов «приморожена» к своим энергетическим уровням, и все они не способны принимать добавочную энергию. В этом обстоятельстве и состоит разгадка ничтожно малой теплоемкости электронного газа. При не слишком высоких температурах воспринимать добавочную энергию («нагреваться») могут лишь очень немногие электроны, энергетические уровни которых расположены в непосредственной близости от свободных уровней. Для их перехода на более высокий свободный уровень нужна лишь энергия ~kT, и такой переход становится возможным. Но при обычных температурах относительное число таких электронов столь мало, что их доля в общей теплоемкости тела остается практически незаметной.
6.2. Успехи зонной теории металлов.
Зонная теория смогла дать ответы, на вопросы, оказавшиеся неразрешимыми в рамках классической электронной теории:
а) и б) В рамках зонной теории получается, что температурная зависимость удельного сопротивления может определяться лишь длиной свободного пробега l. При абсолютном нуле температуры электроны движутся сквозь весь кристалл, не испытывая столкновений. Следовательно, при
.
Причиной этого является волновая природа электрона. При T=0°К ионы металла образуют неподвижную кристаллическую решетку, и электронные волны, огибая ионы, проходят через весь кристалл, не отклоняясь в стороны.
С повышением температуры ионы металла приходят в тепловое колебательное движение, нарушающее идеальную правильность кристаллической решетки. То сближаясь, то удаляясь друг от друга, ионы создают «флуктуации» плотности, на которых происходит рассеивание электронных волн, соответствующее соударениям электронов с кристаллической решеткой. Чем выше температура, тем интенсивнее и чаще возникающие флуктуации кристаллической решетки и тем короче длина свободного пробега электрона. Согласно вычислениям
в полном соответствии с опытом.
в) Найденная методами зонной теории теплоемкость электронного газа получилась равной
,
где – некоторый коэффициент. При обычных температурах это весьма малая величина, так что молярная теплоемкость металла примерно равна теплоемкости кристаллической решетки, что согласуется с опытными данными.
Т. о., современная теория металлов, учитывающая волновые свойства электрона, разъясняет противоречия, возникающие в классической электронной теории, и правильно предсказывает целый ряд новых фактов.
Вопросы для самоконтроля:
1. Сформулируйте принцип Паули.
2. Как, согласно квантовой теории, распределены электроны проводимости металлов по энергиям при Т = 0 °К? Как изменяется это распределение при повышении температуры?
3. Какие зоны называются разрешенными и какие запрещенными?
4. В чем состоит отличие металлов от диэлектриков согласно зонной теории?
5. Как квантовая теория разрешает противоречия между данными экспериментов и результатами классической теории электропроводности металлов?
Тема 3. Ток в жидкостях
Лекция № 7. Электролиз и электролитическая диссоциация.
Цель: выяснить природу и вывести законы электропроводности жидкостей.
Основные понятия:
Электролит – вещество, которое проводит электрический ток вследствие диссоциации на ионы.
Электролиз – совокупность процессов, происходящих при прохождении постоянного электрического тока через электролит с погруженными в него электродами.
Электролитическая диссоциация – процесс распада электролита на ионы при его растворении или плавлении.
Электрохимический эквивалент вещества – количество вещества, которое выделяется на электроде при прохождении через электролит единичного заряда.
Гальванопластика – процесс осаждения слоя металла на поверхности какого-либо предмета.
Гальваностегия – процесс покрытия одного металла другим, более устойчивым в механическом и химическом отношении.
7.1. Электролиз. Электролитическая диссоциация.
Вещества, проводящие ток и при этом разлагающиеся, называют проводниками второго рода, или электролитами, а самое разделение их электрическим током – электролизом (от греч. 1уо – разлагаю). К электролитам относятся растворы кислот, щелочей и солей как в воде, так и в других растворителях. Кроме того, электролитической проводимостью обладают расплавленные соли.
Не следует, однако, думать, что электролитическая проводимость всегда связана с расплавленным или растворенным состоянием вещества. Медь, будучи расплавлена, остается проводником первого рода (проводя ток, она при этом химически не изменяется). Прохождение тока через раствор натрия в жидком аммиаке также не сопровождается процессом разложения. С другой стороны, некоторые соли уже в твердом состоянии, особенно при нагревании, обнаруживают электролитическую проводимость.
Наиболее наглядный пример электролиза твердого тела представляет собой электролиз стекла (сплав натриевой и кальциевой солей кремнекислоты). Анодом (А, рис.) является амальгама (ртутный раствор) натрия, находящаяся в нагретом до 300C фарфоровом тигле, катодом (К) — алюминиевая проволока; g – стеклянная трубка с очень разреженным гелием. Мы имеем, следовательно, цепь: алюминиевый катод – разреженный гелий – нагретое стекло – амальгама натрия (отметим, что при низких температурах стекло – изолятор, а при высоких – проводник электролитического типа). Вследствие большого сопротивления этой цепи источник тока должен давать напряжение не менее 200 В. Как только цепь замкнута, наличие в ней тока обнаруживается свечением гелия наполняющего трубку, а разложение стекла – выделением на внутренней стенке трубки одной из составных частей стекла, натрия, в виде блестящего металлического зеркала (на рис. отмечено пунктиром). Отметим, что электролитической проводимостью обладает именно стекло (разреженный гелий обладает иным типом проводимости).
При электролитической проводимости носителями тока являются ионы. В электролитических растворах расщепление молекул на ионы производится действием растворителя. Каждая полярная молекула растворенного вещества находится в окружении молекул растворителя. Если молекулы растворителя являются также полярными, они будут испытывать вблизи молекулы растворенного вещества ориентирующее действие создаваемого ею электрического поля. Поэтому молекулы растворителя повернутся к положительно заряженной части молекулы растворенного вещества своими отрицательными «концами», а к отрицательно заряженной части – положительными «концами» (рис.; сплошным контуром обведена молекула растворенного вещества, пунктирными контурами – молекулы растворителя). При таком расположении молекул растворителя создаваемое ими поле ослабляет связь между разноименными ионами молекулы растворенного вещества, вследствие чего эта связь может оказаться разорванной за счет энергии теплового движения. В этом случае молекула разделяется на два или большее количество ионов разных знаков. Это явление называется электролитической диссоциацией.
В расплавах и твердых телах при высоких температурах расщепление молекул на ионы (электролитическая диссоциация) происходит под действием температуры (естественно, что никаких «растворителей» в этом случае нет).
Отметим что во всех случаях распад на ионы (электролитическая диссоциация) происходит до включения внешнего электрического поля, которое лишь вызывает упорядоченное движение ионов.
Разность потенциалов на электродах, погруженных в электролит, определяет напряженность электрического поля в электролите и заставляет ионы с отрицательным зарядом (анионы) передвигаться к аноду, с положительным зарядом (катионы) – к катоду. Скорость их движения зависит от природы ионов, от вязкости окружающей среды и от напряжения тока. Чем выше напряжение, тем значительнее скорость ионов. При высоком напряжении и малом удалении друг от друга электродов скорости ионов достигают таких размеров, что возникает искровой разряд. В этом случае свободные ионы, устремляясь к электродам, приобретают столь большую кинетическую энергию, что все встреченные на своем пути молекулы они ударами разбивают на ионы, что влечет за собой резкое увеличение электропроводности и соответственно стремительное возрастание тока. Если разность потенциалов на электродах сравнительно невелика, процесс перенесения электричества протекает менее бурно, соударение ионов с молекулами не вызывает их диссоциации и проявляется только в выделении тепла.
Пусть идет электролиз СиС12 (хлорной меди). К катоду стремятся электроны по металлической цепи и сюда же подходят ионы из раствора электролита. Ион Си++ есть атом меди, лишенный двух электронов; получая их от насыщенного электронами катода, ион Си+ + превращается в незаряженный атом металла. Обозначая свободный электрон через е, мы можем написать реакцию на катоде в такой форме:
Cu+++2e=Cu.
С1– – ионы, имеющие избыточные электроны, притягиваются анодом и передают ему свои избыточные электроны, превращаясь в незаряженные атомы хлора:
2С1–=2С1 + 2е.
Эта нейтрализация ионов на поверхности электродов является необходимым звеном в прохождении тока через гальваническую цепь, так как иначе в электродах и вблизи них в электролитическом растворе скопились бы громадные заряды, противодействующие дальнейшему течению тока.
7.2. Закон Ома.
При движении в электролите ион испытывает силу сопротивления, которая в случае установившегося движения пропорциональна скорости иона. На этом основании ион в электролите можно характеризовать подвижностью b – величиной дрейфовой скорости, приобретаемой ионом под действием постоянного электрического поля Е, равного единице. Подвижности положительных и отрицательных ионов разные. Обозначая их через b+ и b–, а установившиеся скорости ионов – через и
, можем написать
,
.
Что касается концентрации, то она для положительных и отрицательных ионов одинакова, так как раствор электролита остается электрически нейтральным (точнее, квазинейтральным), и равна n, где n – концентрация нейтральных молекул растворенного вещества, а – степень диссоциации. Поэтому плотность тока в электролите определится выражением
.
Так как заряд иона по абсолютной величине равен ze, где е – элементарный заряд, a z – валентность иона, то
.
Данное выражение справедливо лишь на некотором удалении от электродов. В непосредственной близости от электродов ток создается ионами только одного знака: анионами вблизи анода и катионами вблизи катода. Отсюда для удельной электропроводности электролита получаем
.
Данная величина не зависит от . Следовательно, плотность тока в электролитах пропорциональна напряженности поля. Это означает, что для электролитов справедлив закон Ома
.
7.3. Закон Фарадея.
Прямым следствием процесса электролиза является накопление у электродов продуктов химического разложения электролита. Эти продукты разложения электролита могут или оставаться в растворенном состоянии, или отлагаться на электродах, или же выделяться, как при разложении воды, в виде газов.
Количество веществ, выделяющихся при электролизе на электродах, определяется законом, который был экспериментально установлен в 1833 г. Фарадеем: масса m выделенного на каждом электроде вещества пропорциональна заряду Q, прошедшему через электролит:
.
Коэффициент пропорциональности k называют электрохимическим эквивалентом вещества. Он равен отношению массы вещества, выделившегося на электроде при электролизе, к заряду, прошедшему через электролит.
Физический смысл закона Фарадея можно понять, зная механизм ионной проводимости и электролиза. Чем большее количество электричества пройдет через электролит, тем большее число ионов подойдет к электродам. Положительные ионы при соприкосновении с катодом получают недостающие электроны и осаждаются на катоде в виде нейтральных атомов. Отрицательные ионы при соприкосновении с анодом отдают лишние электроны и осаждаются на аноде. Каждый осаждающийся на электроде ион переносит с собой некоторый электрический заряд. Следовательно, полный заряд, переносимый всеми ионами, строго пропорционален полному количеству ионов, осевших на электродах, т. е. массе выделяющегося вещества.
7.4. Применения электролиза.
Электролиз находит самые разнообразные технические применения. Охарактеризуем вкратце некоторые из них.
1. Гальванопластика. В 1837 г. Б. С. Якоби применил электролиз для изготовления металлических слепков с рельефных моделей. Модель из воска или какого-либо другого пластического материала покрывается для создания проводящего слоя графитовым порошком и затем включается в качестве катода при электролизе. Электролитом служит раствор соли, содержащей металл, из которого хотят получить слепок. Металл отлагается на катоде в виде слоя, точно отражающего рельеф модели. Полученный слепок легко отделяется от катода. Таким способом иногда изготовляются типографские клише.
2. Гальваностегия. С помощью электролиза наносят на поверхность металлических изделий тонкий слой другого металла. Это делается с декоративными целями (золочение, серебрение, платинирование), а также для создания антикоррозионных покрытий (никелирование, хромирование, кадмирование и т. п.).
3. Электрометаллургия. Путем электролиза расплавленных руд получают алюминий, натрий, магний, бериллий и некоторые другие металлы. Например, сырьем для получения алюминия служат обычно бокситы – минералы, содержащие глинозем (А12О3). В качестве электродов применяются угольные пластины. Руда поддерживается в расплавленном состоянии за счет тепла, выделяемого при прохождении тока.
Электролиз применяют также для рафинирования (т. е. очистки) металлов. Для этого пластина из очищаемого металла включается в качестве анода соответствующей электролитической ванны. Электролитом служит раствор соли очищаемого металла. При надлежащем выборе напряжения выделяться на катоде будет только данный металл, а примеси выпадут в виде осадка. Таким путем получают, например, очень чистую медь, которая называется электролитической.
4. Электролитическая полировка. Количество вещества, осаждающегося на электроде или переходящего с электрода в раствор, пропорционально плотности тока. У выступов, как мы знаем, напряженность поля Е больше, следовательно, в этих местах больше и плотность тока; во впадинах плотность тока, напротив, бывает меньше. Поэтому, если изделие с шероховатой поверхностью сделать анодом соответствующим образом выбранной электролитической ванны, то с выступов будет переходить в раствор больше металла, чем из впадин, и шероховатости будут сглаживаться. На этом принципе основывается электрополировка металлов.
5. Получение тяжелой воды. Тяжелой водой (D2O) называется вода, в которой атомы водорода замещены атомами дейтерия (D) – изотопа водорода с атомным весом 2. Тяжелая вода присутствует в небольшом количестве в обычной воде. Ионы D+ обладают меньшей подвижностью, чем ионы Н+. Поэтому в выделяющемся при электролизе газе тяжелый водород присутствует в относительно меньшем количестве, чем в исходной воде; в электролите же концентрация тяжелой воды повышается. Если производить электролиз достаточно долго, можно получить воду с высоким содержанием молекул D2O.
6. Электролитические конденсаторы. Если в раствор борной щелочи (смеси борной кислоты и аммиака) погрузить алюминиевые электроды и приложить к ним напряжение, то анод быстро покрывается очень тонким непроводящим слоем окислов алюминия, и ток прекращается. Изолирующий слой поддерживается за счет электролиза и при изменении полярности исчезает. Таким образом, анод и электролит оказываются разделенными тончайшим слоем изолятора и образуют конденсатор весьма большой емкости (емкость конденсатора обратно пропорциональна расстоянию между обкладками).
В «сухих» электролитических конденсаторах электролит изготовляют в виде густой пасты и пропитывают им бумажную прокладку, помещаемую между обкладками. Подобные конденсаторы при небольших размерах обладают емкостью порядка сотен микрофарад. При их включении необходимо строго соблюдать обозначенную полярность. Если электрод с образовавшимся на нем слоем окисла подключить к минусу цепи (т. е. в обратном направлении), то изолирующий слой исчезнет и сила тока резко возрастет, что приведет к разрушению конденсатора. Каждый такой конденсатор бывает рассчитан на определенное предельное напряжение, при превышении которого изолирующий слой пробивается и конденсатор выходит из строя.
Вопросы для самоконтроля:
1. Что такое электролиз?
2. Что называют электролитической диссоциацией?
3. Что такое дрейфовая скорость?
4. Как зависит удельное сопротивление электролитов от температуры и концентрации?
5. Сформулируйте закон Фарадея для электролиза. В чем его физический смысл?
6. Приведите примеры технического применения электролиза.
Тема 4. Ток в газах и вакууме
Лекция № 8. Электропроводность газов. Электрический ток в вакууме.
Цель: выяснить природу и вывести законы электропроводности газов и эмиссии; ознакомиться с основными видами газовых разрядов.
Основные понятия:
Ионизация – процесс образования положительных и отрицательных ионов и свободных электронов из нейтральных атомов или молекул.
Рекомбинация – процесс образования нейтральных атомов или молекул из свободных электронов и положительных ионов либо из отрицательных и положительных ионов.
Работа ионизации – энергия, которую необходимо затратить для ионизации атома (молекулы) газа.
Потенциал ионизации – минимальная разность потенциалов, которую должен пройти электрон в ускоряющем электрическом поле, чтобы приобрести кинетическую энергию, достаточную для ионизации частицы.
Газовый разряд – процесс прохождения электрического тока через газ.
Несамостоятельный разряд – электрический ток в газе, возникающий при наличии внешнего ионизатора.
Самостоятельный разряд – электрический ток в газе, который продолжается после прекращается действия внешнего ионизатора.
Тлеющий разряд – один из видов самостоятельного электрического разряда в газах, формирующийся, как правило, при низком давлении газа и малом токе.
Дуговой разряд – один из видов самостоятельного электрического разряда в газах, горящий практически при любых давлениях газа и отличающийся высокой плотностью тока на катоде и низким катодным падением потенциала.
Коронный разряд – один из видов самостоятельного электрического разряда в газах достаточной плотности, возникающий в резко неоднородном электрическом поле вблизи электродов с большой кривизной поверхности (острия, провода).
Искровой разряд – один из видов самостоятельного электрического разряда в газах, возникающий обычно при давлениях порядка атмосферного и сопровождающийся характерным звуковым эффектом — "треском" искры.
Эмиссия – явление испускания электронов поверхностью металла.
Работа выхода – наименьшая энергия, которую необходимо сообщить электрону для того, чтобы удалить его из металла в вакуум.
Ток насыщения – некое значение тока, по достижении которого, величина тока уже не меняется, несмотря на изменение напряжения (напряженности электрического поля).
8.1. Ионизация и электропроводность газов.
Прохождение электрического тока через газы называется газовым разрядом. В металлах и электролитах носители тока существуют всегда, независимо от процессов, связанных с прохождением тока; электрическое поле лишь обусловливает упорядоченное движение имеющихся зарядов. Газы в нормальном состоянии являются изоляторами, носители тока в них отсутствуют. Проводниками электричества могут быть только ионизованные газы. Помимо нейтральных молекул и атомов в ионизованных газах содержатся заряженные частицы: электроны, положительные и отрицательные ионы.
Носители тока в газах могут возникать в результате внешних воздействий, не связанных с наличием электрического поля. В этом случае говорят о несамостоятельной проводимости газа. Несамостоятельный разряд может быть вызван нагреванием газа до высокой температуры, воздействием ультрафиолетовых или рентгеновских лучей, воздействием излучения радиоактивных веществ, бомбардировкой молекул газа быстро движущимися электронами или ионами и т. д.). Если напряженность поля не велика, то несамостоятельный разряд прекращается, как только перестает действовать внешний фактор ионизации.
Если носители тока возникают в результате тех процессов в газе, которые обусловлены приложенным к газу электрическим полем, проводимость и разряд называются самостоятельными. Отметим, что поле может вызвать ионизацию, в результате которой газ становится проводником, только если его напряженность достаточно велика.
Во всех этих случаях происходит вырывание из электронной оболочки атома или молекулы одного или нескольких электронов. Этот процесс называется ионизацией. Для ионизации атома (или молекулы) необходимо совершить работу против сил взаимодействия между вырываемым электроном и остальными частицами атома (или молекулы). Эта работа называется работой ионизации Ai. Величина работы ионизации зависит от химической природы газа и энергетического состояния вырываемого электрона в атоме или молекуле. Наиболее слабо связаны с ядром внешние (валентные) электроны атома, поэтому для удаления из атома валентного электрона нужно затратить меньшую работу, чем для вырывания любого другого электрона.
Работу ионизации можно характеризовать с помощью потенциала ионизации. Потенциалом ионизации i называется та разность потенциалов, которую должен пройти электрон в ускоряющем электрическом поле для того, чтобы увеличение его энергии было равно работе ионизации:
.
Рассмотрим подробнее процесс ионизации газа под действием движущихся электронов или ионов, получивший название ударной ионизации. Кинетическая энергия заряженной частицы (электрона или иона), прошедшей в ускоряющем электрическом поле разность потенциалов , , где q – заряд частицы. В дальнейшем будем считать, что все ионы одновалентны, т.е.
и
.
Если масса частицы m, то ее скорость v равна
.
Для простоты рассмотрим одноатомный газ. При столкновении частицы с нейтральным атомом газа она передает ему часть своей энергии. Если кинетическая энергия частицы сравнительно мала, то, как показывают опыты, ее соударение с атомом носит характер упругого удара. Энергия, сообщаемая при этом атому, недостаточна для его ионизации. Поэтому бомбардировка атомов газа частицами, обладающими малой энергией, вызывает лишь нагревание газа.
Совершенно иначе происходят соударения с атомами газа частиц, кинетическая энергия которых достаточно велика. В этом случае, как показывают опыты, соударения становятся неупругими и вызывают возбуждение атомов газа, т. е. перевод атома с нормального энергетического уровня на более высокий, или даже ионизацию атомов. Оценим минимальное значение кинетической энергии, которой должна обладать частица для того, чтобы вызвать ударную ионизацию газа. Скорость теплового движения молекул во много раз меньше скорости ионизирующей частицы. Поэтому можно считать, что до удара атом неподвижен. Из закона сохранения импульса при неупругом ударе имеем
,
где М – масса атома, u – скорость частицы и атома после удара. При этом приближенно считаем, что скорость электрона, выбитого из атома, тоже равна u. Начальная кинетическая энергия частицы расходуется при ударе на работу ионизации Ai и сообщение частице и атому кинетической энергии, соответствующей их скорости и после удара:
.
Заменив скорость и ее выражением, найденным из закона сохранения импульса, получим
.
Т. о., минимальная кинетическая энергия, которой должна обладать частица для осуществления ударной ионизации атома газа, не может быть меньше работы ионизации Ai и будет тем ближе к Ai, чем меньше масса частицы по сравнению с массой атома. Для электрона эта энергия меньше, чем для любого иона. Из последней формулы видно, что в одном и том же ускоряющем электрическом поле электрон и одновалентный ион приобретают одинаковую кинетическую энергию. Поэтому для осуществления ударной ионизации ионы должны пройти в ускоряющем электрическом поле большую разность потенциалов, чем электроны. Работа, необходимая для возбуждения атома, меньше работы ионизации. Следовательно, неупругие соударения частиц с атомами газа возможны и при энергии частиц, меньшей той, которая соответствует последней формуле.
Процесс соударения электронов или ионов с молекулами, состоящими из двух и большего числа атомов, качественно подобен рассмотренному нами процессу их соударения с молекулами одноатомных газов. Однако в этом случае следует учитывать, что возбуждение двухатомной и более сложной молекулы может состоять в увеличении не только энергии ее электронов, но и энергии колебаний ядер атомов и энергии вращательного движения молекулы.
Итак, ионизация приводит к освобождению электронов и образованию положительных ионов. Освободившиеся электроны могут присоединяться к нейтральным молекулам и атомам, превращая их в отрицательные ионы. Ионы и свободные электроны делают газ проводником электричества.
После прекращения действия ионизатора положительные и отрицательные ионы газа соединяются между собой с образованием нейтральных молекул и атомов. Этот процесс называется рекомбинацией. В результате рекомбинации проводимость газа пропадает или, во всяком случае, возвращается к своему исходному значению. Проводимость спадает не сразу, а постепенно, так как для полной рекомбинации ионов газа требуется конечное время.
8.2. Несамостоятельный разряд.
Пусть газ, находящийся между плоскими параллельными электродами, подвергается непрерывному постоянному по интенсивности воздействию какого-либо ионизирующего агента (например, рентгеновских лучей). Действие ионизатора приводит к тому, что от некоторых молекул газа отщепляется один или несколько электронов, в результате чего эти молекулы превращаются в положительно заряженные ионы. При не очень низких давлениях отщепившиеся электроны обычно захватываются нейтральными молекулами, которые таким образом становятся отрицательно заряженными ионами. Число пар ионов, возникающих под действием ионизатора за секунду в единице объема, обозначим через .
Наряду с процессом ионизации в газе будет происходить рекомбинация ионов. Количество рекомбинирующих за секунду в единице объема пар ионов обозначим через ; оно пропорционально квадрату числа имеющихся в единице объема пар ионов n:
(r – коэффициент пропорциональности).
В состоянии равновесия должно быть равно
, т. е.
.
Под действием космического излучения и следов радиоактивных веществ, имеющихся в земной коре, в атмосферном воздухе возникает ежесекундно в среднем несколько пар ионов в 1 см3. Равновесная концентрация ионов составляет примерно 103 см–3. Эта концентрация недостаточна для того, чтобы обусловить заметную проводимость. Чистый сухой воздух, как известно, является очень хорошим изолятором.
Если подать напряжение на электроды, то убыль ионов будет происходить не только вследствие рекомбинации, но и за счет отсасывания ионов полем к электродам. Пусть из единицы объема отсасывается ежесекундно пар ионов. Если заряд каждого иона е, то нейтрализация на электродах одной пары ионов сопровождается переносом по цепи заряда, равного е. Каждую секунду электродов достигают
пар ионов (S – площадь электродов, l – расстояние между ними; Sl равно объему межэлектродного пространства). Следовательно, сила тока в цепи равна:
;
откуда
,
где j – плотность тока.
При наличии тока условие равновесия должно быть записано следующим образом:
или
.
Вместе с тем для плотности тока может быть написано выражение, аналогичное выражению для электролитов:
,
где b+ и b– – подвижности положительных и отрицательных ионов. В этом выражении n является функцией j, т. е. в конечном счете функцией Е.
Исключив n из последних двух выражений и решив получающееся квадратное уравнение, можно найти зависимость j(E) (приводить которую здесь не будем ввиду ее сложности).
В случае слабых полей формула для j имеет вид
.
Множитель при Е в данной формуле не зависит от напряженности поля. Следовательно, в случае слабых полей несамостоятельный газовый разряд подчиняется закону Ома.
В случае сильных полей формула для j имеет вид
.
Плотность тока в данном случае создается всеми ионами, порождаемыми ионизатором в заключенном между электродами столбе газа с единичным поперечным сечением. Следовательно, эта плотность тока является наибольшей при данной интенсивности ионизатора и величине межэлектродного промежутка l. Ее называют плотностью тока насыщения jнас.
Если рассчитать плотность тока насыщения jнас при обычных условиях, то можно показать, проводимость воздуха будет очень малой величиной.
Найденная зависимость j(E) изображена на рисунке (сплошная кривая). При достаточно больших значениях напряженности поля ток начинает резко возрастать (см. пунктирный участок кривой). Это объясняется тем, что порождаемые внешним ионизатором электроны за время свободного пробега успевают приобрести энергию, достаточную для того, чтобы, столкнувшись с молекулой, вызвать ее ионизацию (ионизация ударом). Возникшие при этом свободные электроны, разогнавшись, в свою очередь вызывают ионизацию. Таким образом, происходит лавинообразное размножение первичных ионов, созданных внешним ионизатором, и усиление разрядного тока. Однако процесс не утрачивает характера несамостоятельного разряда, так как после прекращения действия внешнего ионизатора разряд продолжается только до тех пор, пока все электроны (первичные и вторичные) не достигнут анода (задняя граница пространства, в котором имеются ионизирующие частицы – электроны, перемещается к аноду).
На использовании несамостоятельного газового разряда основано действие ионизационных камер и счетчиков – приборов, применяемых для обнаружения и счета ядерных частиц, а также для измерения интенсивности рентгеновского и гамма-излучения.
8.3. Самостоятельный разряд.
Для того чтобы газовый разряд стал самостоятельным, необходимо, чтобы в результате самого разряда в газе непрерывно образовывались свободные заряды. Т. к. основным источником их возникновения является ударная ионизация молекул газа, то необходимо наличие двух встречных лавин ионов, что возможно только в том случае, когда ионизацию ударом способны вызвать носители обоих знаков.
В случае, если напряженность электрического поля E между электродами столь велико, что положительные ионы также приобретают способность порождать вторичные электроны. В этом случае образуется двусторонняя лавина электронов и положительных ионов, возникающих во всех частях объема газа. Теперь внешний ионизатор уже не играет практически никакой роли в осуществлении газового разряда, так как число создаваемых им первичных электронов и ионов ничтожно по сравнению с числом вторичных электронов и ионов, образующихся благодаря указанным выше процессам. Поэтому прекращение действия внешнего ионизатора никак не отражается на дальнейшем протекании газового разряда. Таким образом, при достаточно большом увеличении напряженности поля между электродами газоразрядной трубки несамостоятельный газовый разряд может перейти в самостоятельный. Этот переход называется электрическим пробоем газа, а соответствующая ему напряженность поля EЗ – напряженностью зажигания или напряженностью пробоя.
Самостоятельный разряд принимает разнообразные формы в зависимости от давления газа, конфигурации электродов и параметров внешней цепи. Кратко рассмотрим основных виды самостоятельного разряда.
1) Тлеющий разряд возникает при низких давлениях. Его можно наблюдать в стеклянной трубке длиной около 0,5 м, с впаянными у концов плоскими металлическими электродами. На электроды подается напряжение порядка 1000 В. При атмосферном давлении ток через трубку не течет. Если понижать давление в трубке, то примерно при 40 мм рт. ст. возникает разряд в виде светящегося извилистого тонкого шнура, соединяющего анод с катодом. По мере понижения давления шнур утолщается и приблизительно при 5 мм рт. ст. заполняет все сечение трубки – устанавливается тлеющий разряд. Цвет свечения будет зависеть от химической природы газа.
Основные процессы, необходимые для поддержания тлеющего разряда, происходят в его катодной части. Остальные части разряда не существенны, они могут даже отсутствовать (при малом расстоянии между электродами или при низком давлении). Основных процессов два. Это – вторичная электронная эмиссия из катода, обусловленная бомбардировкой его положительными ионами, и ударная ионизация электронами молекул газа.
Явление тлеющего разряда применяется в газосветных трубках, наполненных разреженным гелием или неоном и светящихся при прохождении через них слабого тока при высоком напряжении. Такие трубки широко применяются для различных уличных надписей и реклам, для сигнализации на аэродромах (неоновые маяки), в качестве ламп дневного света.
Тлеющий разряд применяется и для создания электровакуумных приборов – выпрямителей, тиратронов, стабилотронов и др.
2) Дуговой разряд начинается с соприкосновения угольных или металлических электродов. Вследствие большого сопротивления их контакта электроды раскаляются, и с катода начинается электронная эмиссия. Воздушный промежуток между электродами сильно ионизируется высокой температурой и приобретает малое сопротивление. Поэтому после разведения электродов даже при небольшой разности потенциалов возникает большой ток (десятки, сотни ампер и больше). Электроны, бомбардируя анод, выбивают в нем углубление (кратер). При атмосферном давлении температура кратера достигает 4000С, а при повышенном давлении – даже около 6000С (температура поверхности Солнца). Основная часть света дуги исходит именно из кратера анода.
Явление дугового разряда используется в электросварке. При таком способе соединения металлов, металлический электрод, создающий дугу, сам плавился, сваривая металлические швы.
При пониженных давлениях ионизованный газ в дуге остается холодным, как в случае тлеющего разряда. Такая холодная дуга горит в парах ртути над поверхностью жидкой ртути в ртутных выпрямителях и кварцевых лампах.
Дуга использовалась в свече Яблочкова, являвшейся первым электрическим источником света. В дальнейшем ее вытеснила лампа накаливания. Однако в наиболее мощных прожекторах в качестве источника света по-прежнему служит электрическая дуга.
Высокая температура дугового разряда позволяет использовать его для устройства дуговой печи. В настоящее время дуговые печи, питаемые током очень большой силы, применяются в ряде областей промышленности: для выплавки стали, чугуна, ферросплавов, бронзы, получения карбида кальция, окиси азота и т. д.
3) Коронный разряд возникает при нормальном давлении в газе, находящемся в сильно неоднородном электрическом поле (например, около остриев или проводов линий высокого напряжения). При коронном разряде ионизация газа и его свечение происходят лишь вблизи коронирующих электродов. В случае коронирования катода (отрицательная корона) электроны, вызывающие ударную ионизацию молекул газа, выбиваются из катода при бомбардировке его положительными ионами. Если коронирует анод (положительная корона), то рождение электронов происходит вследствие фотоионизации газа вблизи анода. Корона – вредное явление, сопровождающееся утечкой тока и потерей электрической энергии. Для уменьшения коронирования увеличивают радиус кривизны проводников, а их поверхность делают возможно более гладкой. При достаточно высоком напряжении между электродами коронный разряд переходит в искровой.
4) Искровой разряд имеет вид ярких зигзагообразных разветвляющихся нитей-каналов, которые пронизывают разрядный промежуток и исчезают, сменяясь новыми. Исследования показали, что каналы искрового разряда начинают расти иногда от положительного электрода, иногда от отрицательного, а иногда и от какой-либо точки между электродами. Это объясняется тем, что ионизация ударом в случае искрового разряда происходит не по всему объему газа, а по отдельным каналам, проходящим в тех местах, в которых концентрация ионов случайно оказалась наибольшей. Искровой разряд сопровождается выделением большого количества теплоты, ярким свечением газа, треском или громом. Все эти явления вызываются электронными и ионными лавинами, которые возникают в искровых каналах и приводят к огромному увеличению давления, достигающему 107 – 108 Па, и повышению температуры до 10 000°С.
Характерным примером искрового разряда является молния. Главный канал молнии имеет диаметр от 10 до 25 см, а длина молнии может достигать нескольких километров. Максимальная сила тока импульса молнии достигает десятков и сотен тысяч ампер.
8.4. Электрический ток в вакууме.
Под вакуумом понимают такую степень разрежения газа в сосуде, при которой длина свободного пробега молекулы в сосуде становится больше линейных размеров сосуда и соударениями между молекулами газа можно пренебречь. При такой степени разрежения самостоятельного газового разряда происходить не может. Чтобы в вакуумной трубке, имеющей два электрода – катод и анод, – протекал электрический ток, необходимо каким-либо способом внести туда заряженные частицы.
Существует несколько способов сообщения электронам дополнительной энергии, необходимой для удаления их из металла: нагревание, облучение видимым или ультрафиолетовым светом, воздействие сильного внешнего поля, бомбардировка металлов частицами. Под воздействием этих факторов может происходить явление электронной эмиссии.
В различных электронных приборах применяются все виды эмиссии, но чаще всего используется наиболее удобно управляемая термоэлектронная эмиссия.
Термоэлектронной эмиссией называется испускание электронов нагретыми металлами.
Явление термоэлектронной эмиссии объясняется тем, что вследствие распределения по энергиям имеется некоторое количество электронов, энергия которых достаточна для того, чтобы преодолеть работу выхода из металла (Работой выхода называется наименьшая энергия, которую необходимо сообщить электрону для того, чтобы удалить его из металла в вакуум). При повышении температуры количество таких электронов резко возрастает и делается вполне заметным.
Исследование термоэлектронной эмиссии удобно производить с помощью двухэлектродной лампы, называемой также вакуумным диодом. Она представляет собой хорошо откачанный металлический или стеклянный баллон, внутри которого имеются два электрода – катод К и анод А. Конструктивно электроды могут быть выполнены разными способами. В простейшем случае катод имеет форму тонкой прямой нити, анод – коаксиального с ней цилиндра.
Если установить постоянный накал катода и снять зависимость силы анодного тока ia от анодного напряжения Ua, то получается кривая, изображенная на рисунке (различные кривые соответствуют разным температурам катода). Эта кривая называется вольт-амперной характеристикой.
При Ua = 0 вылетевшие из катода электроны образуют вокруг него отрицательный пространственный заряд – электронное облако. Это облако отталкивает вылетающие из катода электроны и большую часть их возвращает обратно. Все же небольшому числу электронов удается долететь до анода, в результате чего в анодной цепи будет течь слабый ток. Чтобы полностью прекратить попадание на анод электронов, т. е. сделать ia равным нулю, необходимо приложить между катодом и анодом некоторое отрицательное напряжение. Следовательно, вольт-амперная характеристика диода начинается не в нуле, а немного левее начала координат.
При малых положительных значениях сила анодного тока изменяется пропорционально Ua3/2 . Теоретически эта зависимость была получена Ленгмюром и Богуславским и называется законом трех вторых.
По мере роста Ua все большее число электронов отсасывается электрическим полем к аноду и, наконец, при определенном значении Ua электронное облако полностью рассасывается и все вылетевшие из катода электроны получают возможность достигнуть анода. Дальнейший рост Ua не может увеличить силу анодного тока – ток достигает насыщения.
Очевидно, что именно ток насыщения характеризует термоэлектронную эмиссию. Зависимость плотности тока насыщения от температуры задается формулой (график данной зависимости показан на рисунке):
где Авых – работа выхода, В – не зависящая от рода металла константа.
Как следует из данной формулы, уменьшение Авых повышает эмиссию (легко убедиться в том, что при 1160 К, т. е. при kT = 0,10 эВ, уменьшение Авых от 3 до 1 эВ приводит к возрастанию jнас почти в 5108 раз). Поэтому при изготовлении электронных ламп применяются специальные покрытия и способы обработки катодов, приводящие к снижению работы выхода. Современные так называемые оксидные катоды, изготовляемые из никеля, покрытого окисью бария или стронция, имеют работу выхода порядка 1,0 – 1,2 эВ.
Термоэлектронная эмиссия получила наиболее широкую область применения в электронных лампах, которые имеют разнообразное радиотехническое назначение и различное устройство, но вместе с тем имеют одну общую черту. А именно, в электронных лампах в отличие от других термоэлектронных приборов так размещают электроды, чтобы создаваемое ими поле, налагаясь на поле пространственного заряда (облака электронов у поверхности накаленного катода), позволяло бы при небольших изменениях напряжения, подводимого к вспомогательным электродам, получать резкие и возможно большие изменения величины термоэлектронного тока, проходящего через лампу. С этой целью аноды и дополнительные сетчатые электроды электронных ламп устраивают обычно в виде коаксиальных цилиндров строго рассчитанных размеров и помещают накаливаемый катод по оси цилиндра.
Электронные лампы массово использовались в ХХ веке как активные элементы электронной аппаратуры (усилители, генераторы, детекторы, переключатели и т. п.). В настоящее время практически полностью вытеснены полупроводниковыми приборами. Тем не менее, остались еще области, в которых применяются электронные лампы.
1) Одно из важных применений термоэлектронной эмиссии – «электронная пушка», служащая для получения электронного луча в катодных осциллографах. В электронной пушке электроны, испускаемые накаленным катодом, получают значительное ускорение в электрическом поле между катодом и кольцевыми анодами. Этот метод ускорения электронного потока применяется во многих электронных приборах и, в частности, в высоковольтных (на миллионы вольт) электронных трубках, предназначенных для атомно-ядерных исследований.
2) Высокочастотная и высоковольтная мощная техника.
В мощных радиовещательных передатчиках (от 100 Вт до единиц мегаватт) в выходных каскадах применяются мощные и сверхмощные лампы с воздушным или водяным охлаждением анода и высоким (более 100 А) током накала. Магнетроны, клистроны, лампы бегущей волны обеспечивают сочетание высоких частот, мощностей и приемлемой стоимости (а зачастую другая элементная база в принципе неосуществима).
Магнетрон можно встретить не только в радаре, но и в любой микроволновой печи.
Высоковольтные (на миллионы вольт) электронные трубки, предназначенные для атомно-ядерных исследований, используют для значительного ускорения электронов, испускаемых раскаленным катодом.
При необходимости выпрямления или быстрой коммутации значительного тока, которую невозможно осуществлять механическими ключами, необходимо использовать радиолампы. Так, кенотрон обеспечивает приемлемую динамику на напряжениях до миллиона вольт.
3) Военная промышленность.Из-за принципа действия электронные лампы являются устройствами, значительно более устойчивыми к таким поражающим факторам, как электромагнитный импульс. В единственном устройстве может быть несколько сотен ламп. В СССР для применения в бортовой военной аппаратуре в 1950-е годы были разработаны стержневые лампы, отличавшиеся малыми размерами и большой механической прочностью.
4) Космическая техника.Радиационная деградация полупроводниковых материалов и наличие естественного вакуума межпланетной среды делает применение некоторых типов ламп средством повышения надёжности и долговечности космических аппаратов. Применение в АМС Луна-3 транзисторов было связано с большим риском.
5) Повышенная температура среды и радиация.Ламповое оборудование может быть рассчитано на больший температурный и радиационный диапазон условий, нежели полупроводниковое.
6) Звукотехническая аппаратура.Электронные лампы до сих пор находят применение в звукотехнике, как любительской, так и профессиональной. Конструирование ламповых звукотехнических устройств является одним из направлений современного радиолюбительского движения.
Вопросы для самоконтроля:
1. В чем состоит ионизация газа и чем она может быть вызвана?
2. Что называется работой ионизации и потенциалом ионизации и от чего они зависят?
3. Одинаковые ли разности потенциалов должны пройти в ускоряющем электрическом поле электроны и ионы, чтобы приобрести энергию, достаточную для ударной ионизации молекул одного и того же газа?
4. Изложите сущность физических процессов, происходящих при несамостоятельном газовом разряде. Чем объясняется существование тока насыщения?
5. В чем отличие самостоятельного газового разряда от несамостоятельного и каково необходимое условие его существования?
6. Перечислите известные вам типы самостоятельных газовых разрядов. В чем состоят их особенности? Где они применяются?
7. Что называется работой выхода электрона из металла?
8. В чем состоит явление термоэлектронной эмиссии? Объясните зависимость термоэлектронного тока от анодного напряжения.
ЛИТЕРАТУРА
Бутиков Е. И., Кондратьев А. С. Физика для углубленного изучения, т. 2. Электродинамика. Оптика. М., 2004 г.
Васильев А. Э. Курс общей физики. Электричество и магнетизм. СПб., 2003 г.
Гершензон Е. М., Малов Н. Н., Мансуров А. Н. Электродинамика. М., 2002 г.
Калашников С. Г. Электричество. М., 2003 г.
Огурцов А. Н. Лекции по физике. Электричество. М., 2004 г.
Ревинская О.Г., Кравченко Н. С. Электростатическое поле. Томск, 2014 г.
Дмитриева В. Ф. Физика. М., 2005 г.

 Получите свидетельство
Получите свидетельство Вход
Вход












 КОНСПЕКТ ЛЕКЦИЙ по физике для студентов 1-2 курсов специальностей технического профиля СПО Раздел 2. Постоянный ток (508.29 KB)
КОНСПЕКТ ЛЕКЦИЙ по физике для студентов 1-2 курсов специальностей технического профиля СПО Раздел 2. Постоянный ток (508.29 KB)
 0
0 552
552 17
17 Нравится
0
Нравится
0


