Сценарий урока математики
в 6 классе на основе технологии деятельностного метода
Абубакиров Ж.А.,
учитель математики
МБОУ Огнеупорненская сош
Тема: «Сложение и вычитание дробей с разными знаменателями»
Цель урока: построить алгоритм сложения и вычитания дробей с разными знаменателями, тренировать способность к его практическому использованию
Тип урока: урок открытия новых знаний.
Технологии: технология деятельностного метода, информационно-коммуникационные, здоровьесберегающие технологии.
Методы обучения: частично-поисковый, репродуктивный.
.Форма организации учебной деятельности: фронтальная, индивидуальная, работа в парах
Оборудование урока: компьютер, мультимедийный проектор, раздаточный материал , презентация к уроку
Девиз урока: «Дорогу осилит идущий, а математику – мыслящий».
Структура урока:
Самоопределение к учебной деятельности.
Актуализация опорных знаний и фиксация затруднений.
Выявление места и причины затруднения.
Построение проекта выхода из затруднения.
Первичное закрепление во внешней речи.
Самостоятельная работа с проверкой по эталону.
Рефлексия деятельности на уроке.
Постановка домашнего задания с комментированием.
I.Самоопределение к учебной деятельности
Формируемые УУД:
Личностные: самоопределение, смыслообразование
Регулятивные: целеполагание
Коммуникативные: планирование учебного сотрудничества
Цель: включить учащихся в учебную деятельность; определить содержательные рамки урока (продолжение работы с обыкновенными дробями)
.
| Деятельность учителя | Деятельность ученика |
| Ребята, а как вы думаете, что нам на уроке сегодня пригодится? | Ответы детей (удача, знания) |
| А еще сегодня нам пригодятся: | Слушают |
| Откройте тетради. Запишите число. Классная работа. А девизом нашего урока будут такие слова: «Дорогу осилит идущий, а математику – мыслящий». Слайд1 | Записывают |
| Какой темой мы начали заниматься в этой четверти? | Отвечают (обыкновенными дробями)
|
| Чему мы уже научились? | Отвечают (сокращать дроби, отмечать их на координатном луче, приводить к НОЗ, сравнивать дроби с разными знаменателями)
|
| Как вы думаете, куда дальше в изучении дробей мы продолжим продвигаться? | Отвечают (мы должны научиться производить с ними арифметические действия.)
|
II.Актуализация знаний и фиксация затруднений
Формируемые УУД:
Познавательные: анализ, сравнение, аналогия, использование знаковой системы, осознанное построение речевого высказывания, подведение под понятие
Регулятивные: выполнение пробного учебного действия, фиксация индивидуального затруднения, волевая саморегуляция в ситуации затруднения
Коммуникативные: выражение своих мыслей, аргументация своего мнения, учёт разных мнений учащихся
Цель: 1) актуализировать учебное содержание, необходимое и достаточное для восприятия нового материала: основное свойство дроби, приведение дробей к одинаковому знаменателю, сложение и вычитание дробей с одинаковыми знаменателями;
2) актуализировать мыслительные операции, необходимые и достаточные для восприятия нового материала: сравнение, анализ, обобщение;
3) зафиксировать все повторяемые понятия и алгоритмы в виде схем и символов: в виде свойств и определения;
4) зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно значимом уровне недостаточность имеющихся знаний: сложить и вычесть дроби с разными знаменателями.
| Деятельность учителя | Деятельность ученика |
| А начнём мы как всегда с устной работы, потому что чтобы узнать что-то новое …(необходимо повторить уже изученный материал)
|
|
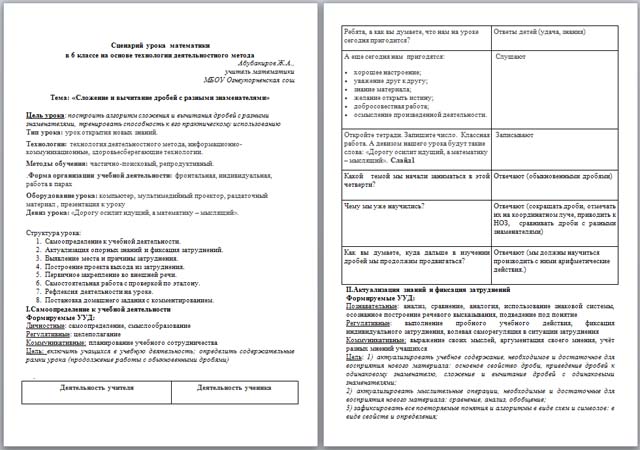
Сократите дроби: 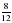 , , 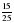 , , 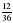 , , 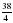 Слайд2 Слайд2
| Выполняют задание |
Выделите целую часть из дробей: 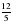 , , 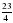 , , 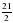 , , 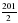 Слайд2 | Выполняют задание |
Дан ряд дробей: 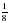 , , 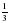 , , 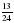 , ,  Слайд2 Слайд2 Что мы можем о нём сказать? К какому НОЗ можно привести все дроби? Почему?
| к 24, т.к. 24 – НОК всех знаменателей Выполняют задания |
| А каким правилом сложения и вычитания дробей вы воспользовались? Запишите его в общем виде для дробей 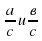 Слайд2 Слайд2 | Письменно выполняют задания Отвечают (Правилом сложения и вычитания дробей с одинаковыми знаменателями. Записывают 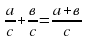 ) )
|
| Давайте восстановим алгоритм сложения и вычитания дробей с одинаковыми знаменателями Нам с вами вразброс даны части алгоритма по сложению и вычитанию дробей с равными знаменателями. Работая в парах, обсудите , восстановите алгоритм по шагам.
| Работают в парах. Составляют алгоритм |
| Алгоритм 1.Сложить (или вычесть) числители и записать результат в числитель суммы (или разности) 2.Знаменатель оставить без изменения, записав его в знаменатель суммы (или разности) 3.Если возможно, сократить полученную дробь и выделить из нее целую часть Слайд3 | Читают алгоритм |
| Хорошо. Следующее задание: выполните действия: 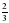 + + 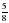 ; ; 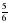 - - 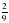 . Предлагаю поработать в парах. Время выполнения: 5 минут. . Предлагаю поработать в парах. Время выполнения: 5 минут. (После завершения работы защита своих работ) Слайд4 | Работают в парах. Выполняют задания |
III. Выявление места и причины затруднения
Формируемые УУД:
Познавательные: анализ, сравнение, обобщение, подведение под понятие, постановка и формулирование проблемы, построение речевого высказывания
Регулятивные: волевая саморегуляция в ситуации затруднения
Коммуникативные: выражение своих мыслей, аргументация своего мнения, учёт разных мнений, разрешение конфликтной ситуации
Цель: 1) организовать коммуникативное взаимодействие, в ходе которого выявляется и фиксируется отличительное свойство задания, вызвавшего затруднение в учебной деятельности;
2) согласовать цель и тему урока.
| Деятельность учителя | Деятельность ученика |
| Почему у вас получились такие разные ответы, как выяснить, кто выполнил задание правильно, а кто-то совсем не дали ответы, Чем отличается предыдущее задание, с которым вы все хорошо справились от этого? | Отвечают (В предыдущем задании дроби были с одинаковыми знаменателями, и у нас был алгоритм сложения и вычитания таких дробей, а в последнем задании у дробей разные знаменатели.)
|
| Что же нам надо сделать, чтобы выполнить задание, определить, кто его выполнил правильно? | Отвечают (Надо найти способ нахождения суммы и разности дробей с разными знаменателями, построить для таких дробей алгоритм сложения и вычитания.)
|
| Сформулируйте цели урока | Сформулируют (Построить алгоритм сложения и вычитания дробей с разными знаменателями, научиться выполнять действия по построенному алгоритму). |
| Хорошо! Чтобы продолжить работу, надо записать тему урока, что мы запишем в тетрадь? | Отвечают (Сложение и вычитание дробей с разными знаменателями) |
| Запишите тему Слайд5 | На экране открывается тема урока. Записывают |
IV. Построение проекта выхода из затруднения
Формируемые УУД:
Личностные: самоопределение, смыслообразование
Познавательные: анализ, синтез, обобщение, аналогия, самостоятельное выделение и формулирование познавательной цели, поиск и выделение необходимой информации, проблема выбора эффективного способа решения, планирование, выдвижение гипотез и их обоснование, создание способа решения проблемы
Регулятивные: волевая саморегуляция в ситуации затруднения
Коммуникативные: выражение своих мыслей, аргументирование своего мнения, учёт разных мнений, планирование учебного сотрудничества со сверстниками, достижение общего решения.
Цель: 1) организовать коммуникативное взаимодействие для построения нового способа действия, устраняющего причину выявленного затруднения;
2) зафиксировать новый способ действия в знаковой, вербальной форме и с помощью эталона.
| Деятельность учителя | Деятельность ученика |
| Задания парам следующее: дополнить известный алгоритм шагом или шагами, чтобы можно было по нему выполнить сложение и вычитание дробей с разными знаменателям и показать на предложенных примерах, как он действует. У каждой группы на столе таблички из старого алгоритма и части нового алгоритма. На работу отводится 7 минут. Все варианты обсуждаются. Результатом обсуждения является алгоритм сложения и вычитания дробей с разными знаменателями. Слайд6 | Работают в парах. Составляют алгоритм |
| Алгоритм Слайд7 Найти НОЗ дробей Найти дополнительный множитель для каждой дроби Умножить числитель и знаменатель каждой дроби на её дополнительный множитель 4.Сложить (или вычесть) числители и записать результат в числитель суммы (или разности) 5.Знаменатель оставить без изменения, записав его в знаменатель суммы (или разности) 6.Если возможно, сократить полученную дробь и выделить из нее целую часть
| Читают алгоритм |
| Вернёмся к нашим выражениям и найдём их значения, используя полученный алгоритм: (будьте внимательны при оформлении задания)
| а) 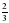 + + 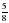 = = 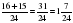 1. найдем НОЗ – НОК знаменателей, НОК (3,8)=24 2. дополнительный множитель для первой дроби равен 8, для второй дроби – 3. 3. складываем числители, знаменатель оставляем без изменения. Дробь неправильная, выделим из неё целую часть.
|
| Физкультминутка Слайд8 | Выполняют физические упражнения |
V. Первичное закрепление во внешней речи
Формируемые УУД:
Личностные: осознание ответственности за общее дело
Познавательные: выполнение действий по алгоритму, построение логической цепи рассуждений, анализ, обобщение, подведение под понятие
Коммуникативные: выражение своих мыслей, использование речевых средств для решения коммуникационных задач, достижение договорённости и согласование общего решения
Цель: зафиксировать изученное учебное содержание во внешней речи.
Ученики решают у доски, используя алгоритм (обратить внимание на проговаривание)
№ 319 (в) Слайд9
в) 
Найдем НОЗ, для этого найдём НОК (4; 5)
НОК (4; 5) = 20
Дополнительный множитель первой дроби 4, второй дроби 5
 =
= 
Применим алгоритм сложения дробей с одинаковыми знаменателями, складываем числители, знаменатели оставляем без изменения
 =
=  =
= 
Дробь неправильная, выделим из неё целую часть

№ 321(г) Проводим аналогичные рассуждения

№ 321 (д, ж) – работа в парах, после выполнения проводится самопроверка по образцу. Сдайд10
д)  ;
;
ж) 
Кто справился с первым заданием? Где допущена ошибка?
Кто справился со вторым заданием? Где допущена ошибка?
Повторим ещё раз алгоритм сложения и вычитания дробей с разными знаменателями.
VI.Самостоятельная работа с проверкой по эталону
Формируемые УУД:
Познавательные: анализ, синтез, аналогия, классификация, подведение под понятие, выполнение действий по алгоритму
Регулятивные: контроль, коррекция, самооценка
Цель: проверить своё умение применять алгоритм сложения и вычитания в типовых условиях на основе сопоставления своего решения с эталоном для самопроверки.
А сейчас каждый проверит сам себя – насколько он сам понял алгоритм сложения и вычитания и может его применить. Самостоятельная работа Слайд11
Ответы для выполнения самопроверки.
После выполнения работы учащиеся проверяют свои ответы и отмечают правильно решённые примеры, исправляют допущенные ошибки, проводится выявление причин допущенных ошибок.
С двумя учащимися индивидуальная работа по карточкам Г.Г. Левитаса.
VII. Рефлексия деятельности на уроке
Цель: 1) зафиксировать новое содержание, изученное на уроке: алгоритм сложения и вычитания дробей;
2) оценить собственную деятельность на уроке;
3) поблагодарить одноклассников, которые помогли получить результат урока;
4) зафиксировать неразрешённые затруднения как направления будущей учебной деятельности: действия со смешанными числами;
5) обсудить и записать домашнее задание.
Формируемые УУД:
Регулятивные: рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности, адекватное понимание причин успеха или неуспеха
Коммуникативные: аргументация своего мнения, планирование учебного сотрудничества
– Что нового узнали на уроке? Слайд12
– Какую цель мы ставили в начале урока?
– Наша цель достигнута?
– Что нам помогло справиться с затруднением?
– Какие знания нам пригодились при выполнении заданий на уроке?
– Как вы можете оценить свою работу?
Постановка домашнего задания с комментированием: алгоритм учить (раздать каждому), п.11,
№ 360(б,д,з,л,о),363,355 (по желанию) Слайд13
Список литературы:
Программа «Учусь учиться» курса математики для 5-6 классов средней школы по образовательной системе деятельностного метода обучения «Школа 2000…», М.: ACADEMIA АПКиППРО, 2007 г.
Асмолов А.Г. Формирование универсальных учебных действий в основной школе: от действия к мысли. Система заданий: пособие для учителя/под. ред. А.Г. Асмолова. – М: Просвещение, 2010
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6 класс. –М: Мнемозина, 2013
Выговская В.В. Поурочные разработки по математике 6 класс Москва «ВАКО» - 2011

 Получите свидетельство
Получите свидетельство Вход
Вход



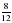 ,
, 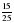 ,
,  ,
, 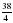 Слайд2
Слайд2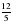 ,
, 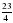 ,
, 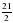 ,
, 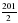
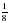 ,
, 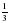 ,
, 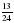 ,
,  Слайд2
Слайд2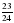 +
+ 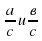 Слайд2
Слайд2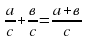 )
)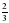 +
+ 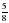 ;
; 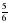 -
- 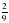 . Предлагаю поработать в парах. Время выполнения: 5 минут.
. Предлагаю поработать в парах. Время выполнения: 5 минут.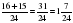









 Конспект урока по математике по теме "Сложение и вычитание дробей с разными знаменателями" (76.02 КB)
Конспект урока по математике по теме "Сложение и вычитание дробей с разными знаменателями" (76.02 КB)
 0
0 562
562 66
66 Нравится
0
Нравится
0


