Автор: Симатова Марина Юрьевна - учитель математики МОУ СОШ № 12 г. Челябинска.
Урок - обобщения
Тема: "Решение иррациональных уравнений". 10 класс
Общие цели урока:
1. Продолжить формирование понятия иррационального уравнения, обобщить способы решения иррациональных уравнений.
2. Отработать правильность применения алгоритма решения иррационального уравнения.
3. Формирование правильной самооценки своего уровня освоенности предметного материала.
4. Формирование приемов самокоррекции, как обнаружении пробелов в понимании материала, так и умение выстроить программу своей коррекции.
Оборудование:
1. Мультимедийный комплекс.
2. Компьютерная презентация для проведения математического диктанта.
3. Компьютерная презентация для проведения самостоятельной работы:
ВАРИАНТ А1, Б1, В1
ВАРИАНТ А2, Б2, В2
4. Компьютерная презентация с решениями самостоятельной работы:
Решение варианта А1, Б1, В1 самостоятельной работы
Решение варианта А2, Б2, В2 самостоятельной работы
5. Компьютерная презентация с дополнительными заданиями.
Ход урока.
I. Орг. момент (1-2 мин.)
II. Математический диктант (5 мин. + 2 мин. проверка)
Цель: Самопроверка и коррекция понятия решение иррационального уравнения.
| I вариант | II вариант |
| 1. Определите промежуток, в котором лежит корень уравнения: |
| 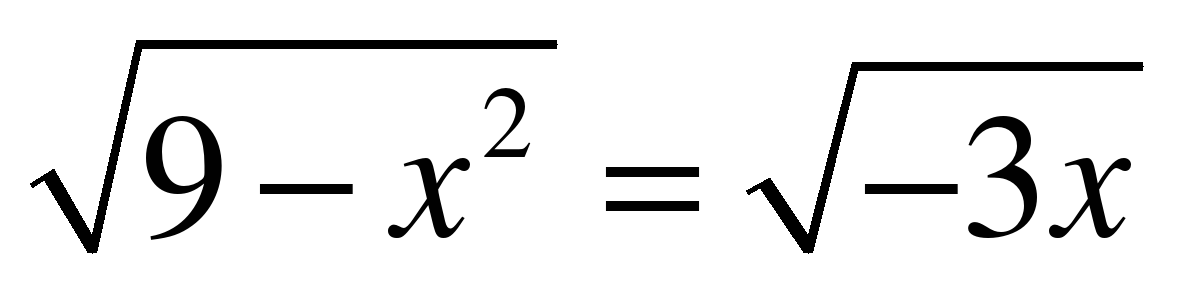
[-3;0] | 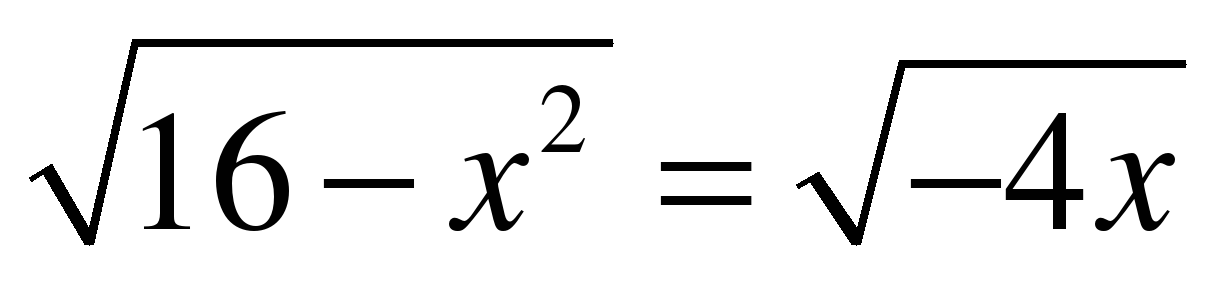
[-4;0] |
| 2. Определите, истинно или ложно высказывание: |
| Если х=3 является корнем уравнения 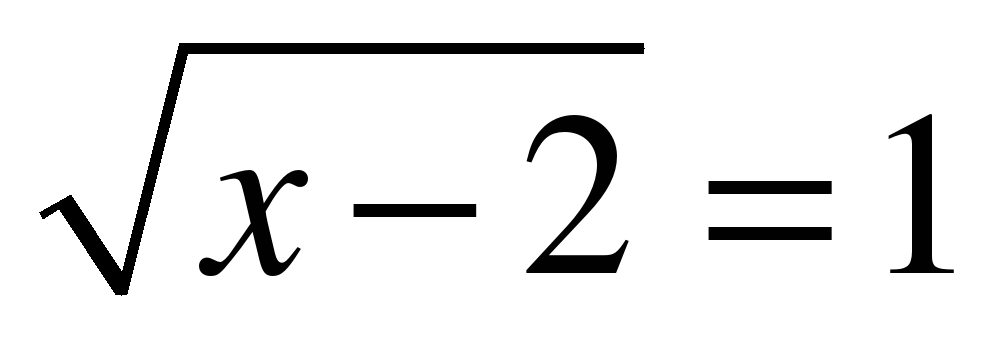 , то x , то x ложь, т. к x 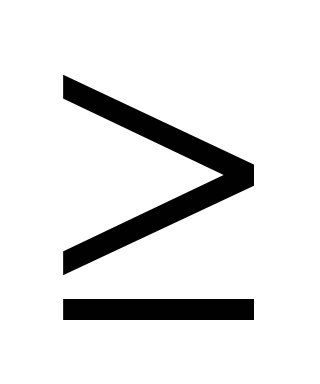 2 2 | Если х=-1 является корнем уравнения 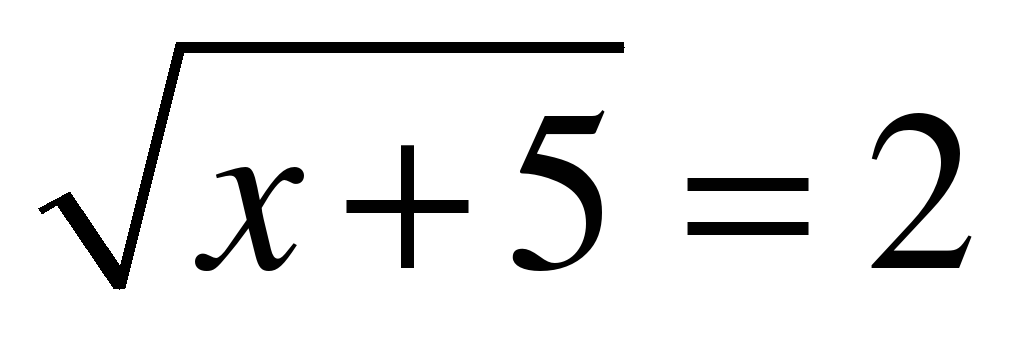 , то х , то х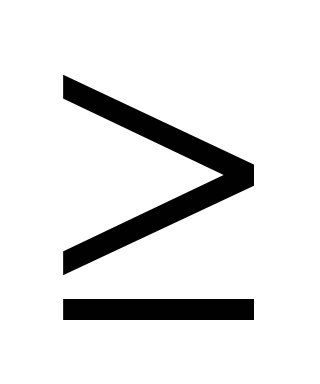 -5 -5 Истина, т.к. х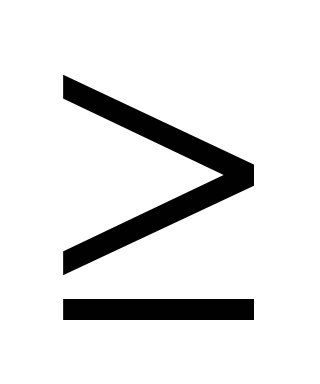 -5 -5 |
| 3. Закончите предложение: |
| Уравнение 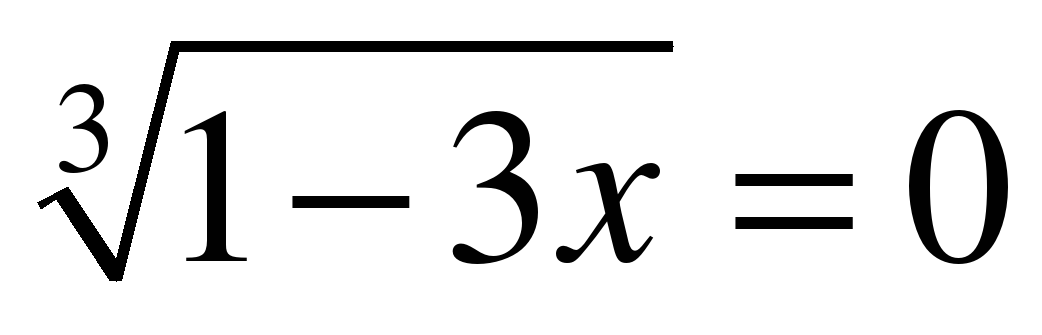 имеет корень равный … имеет корень равный … х=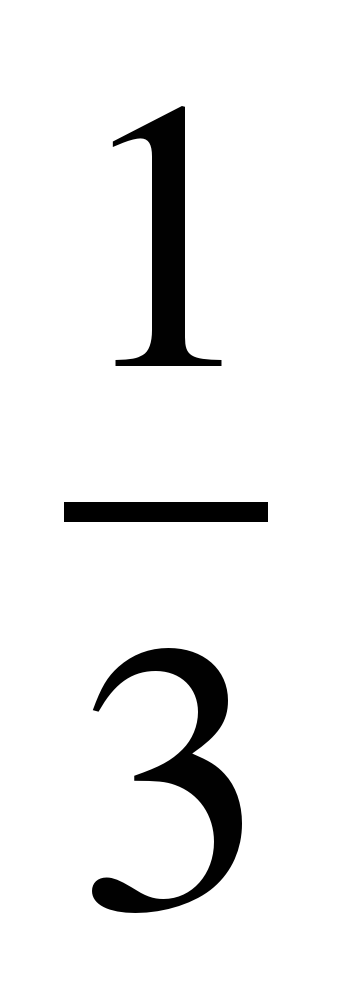 | Уравнение 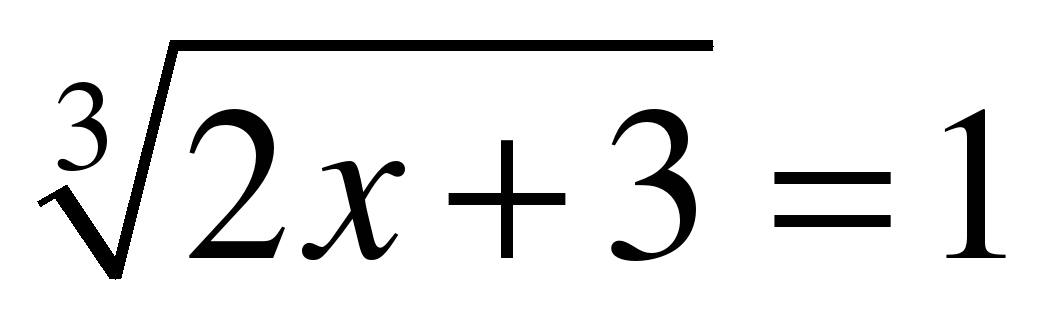 имеет корень равный … имеет корень равный … х=-1 |
| 4. Укажите какому промежутку принадлежит корень уравнения: |
| 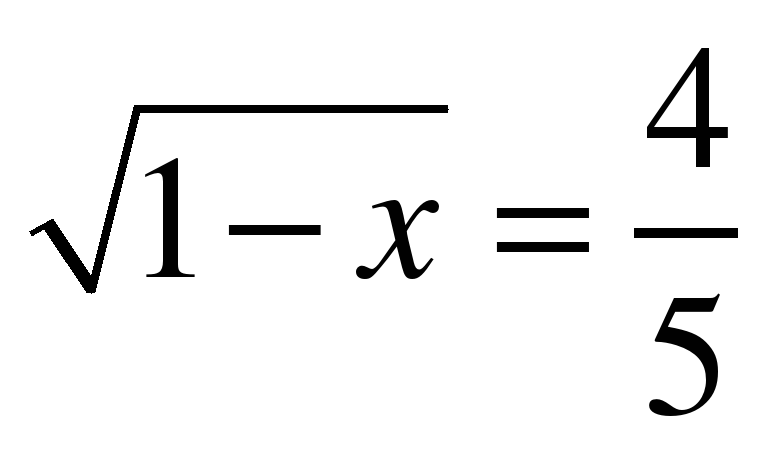
х (- (- ;1] ;1] | 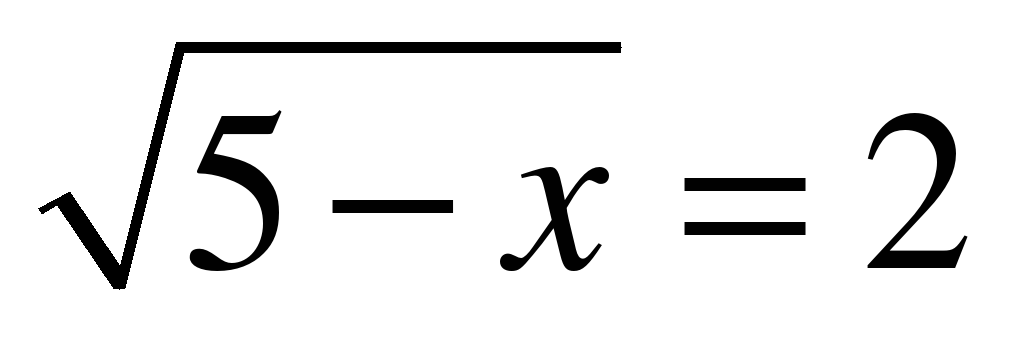
х (- (- ;5] ;5] |
| 5. Найдите сумму корней уравнения: |
| 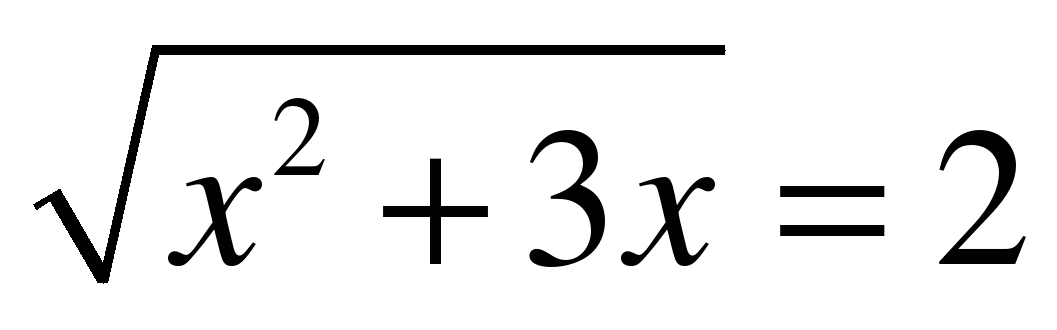
-3 | 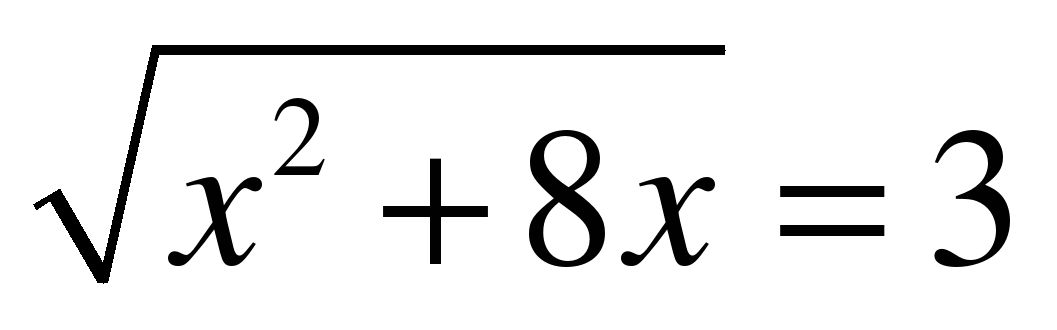
-8 |
Проверка по готовым ответам (Презентация на компьютере с проектором или демонстрационным телевизором). За каждый правильный ответ ученик получает 1 балл. Максимальное количество баллов - 5. Ученики считают количество баллов выполнения работы. Если учащийся набирает 0-2 балла, ему рекомендуется выполнять вариант А, 3-4 балла ему рекомендуется выполнять вариант Б, если 5 баллов – вариант В.
III. Самостоятельная работа.
Цель: проверка умения решать иррациональные уравнения.
Состоит из 2 вариантов, в каждом из которых 3 уровня сложности:
Уровень А - репродуктивный уровень.
Уровень Б - конструктивный уровень.
Урвень В – продуктивный уровень.
Самостоятельная работа
Иррациональные уравнения
| Вариант А1 | Вариант А2 |
| 1. Решите уравнения: |
| а) 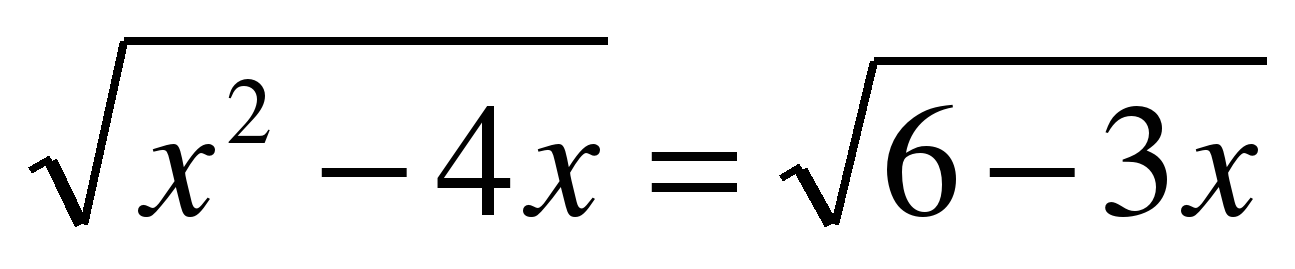 ; ; б) 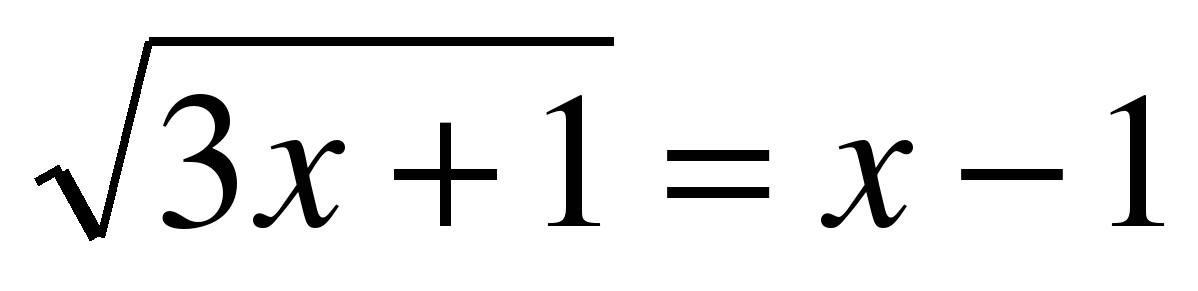 ; ; в) 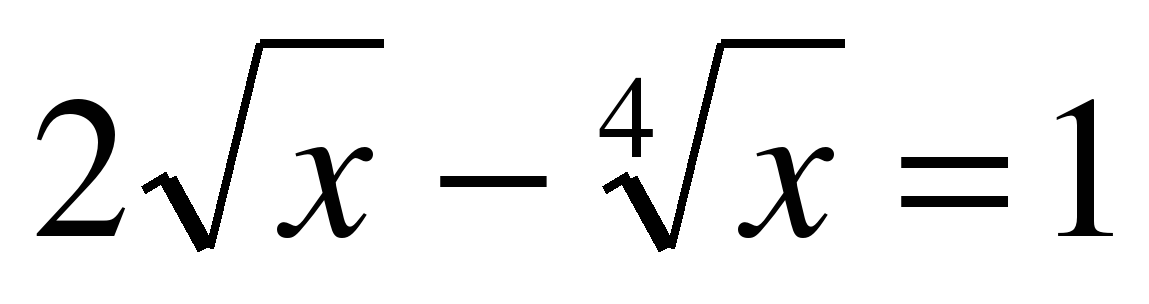 ; ; г) 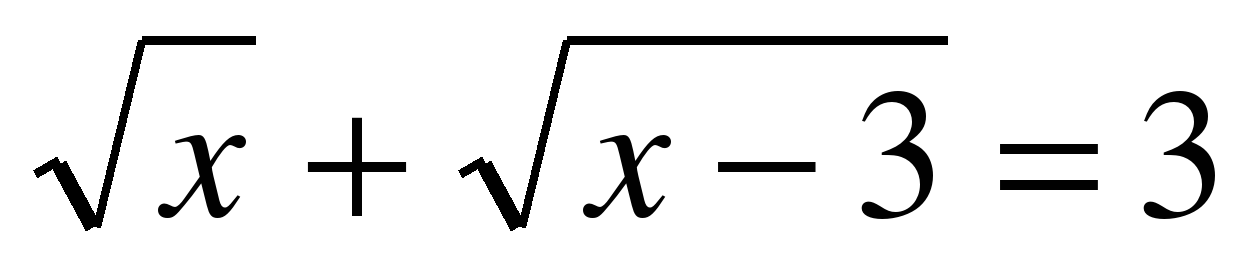 . . | а) 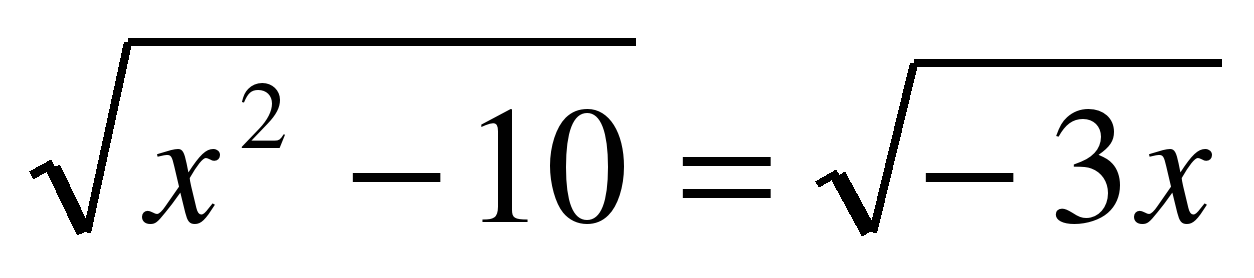 ; ; б) 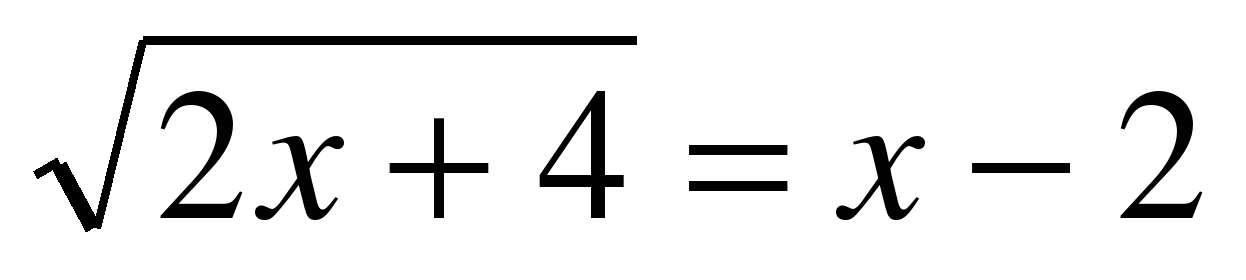 ; ; в) 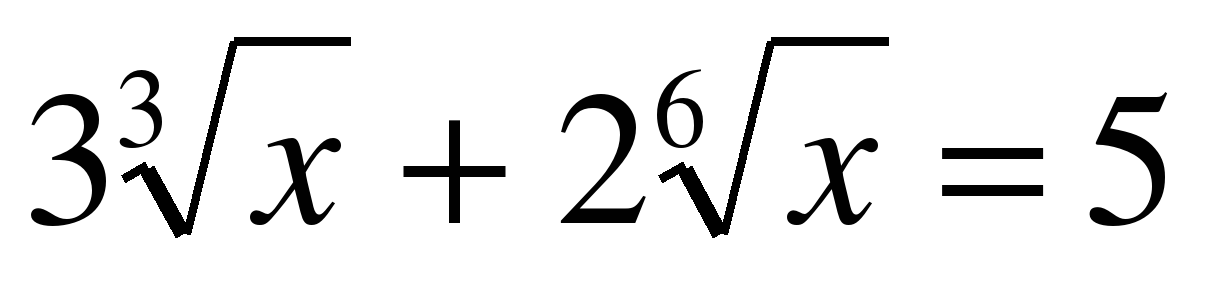 ; ; г) . |
| 2. Определите при каких значениях х |
| функция у=принимает значение, равное 2. | Функция у=принимает значение, равное 3. |
| Вариант Б1 | Вариант Б2 |
| 1. Решите уравнения: |
| а) ; б) ; в) ; г) . | а) ; б) ; в) ; г) . |
| 2. Найдите абсциссу точки пересечения графиков функций |
| у= и у= | у= и у= |
| Вариант В1 | Вариант В2 |
| 1. Решите уравнения: |
| а) ; б) ; в) ; г) . | а) ; б) ; в) ; г) . |
| 2. Найдите точки пересечения графиков функций |
| у= и у= | у= и у= |
Каждый ученик определяет уровень сложности самостоятельной работы сам и должен выполнить из этой работы 2 задания из трех. Каждое задание уровня А оценивается в 1 балл, уровня Б - в 2 балла, уровня В - в 4 балла.
Учитель дает рекомендации по правильному выбору заданий для решения в соответствии со своими самооценками. Проверка самостоятельной работы по готовым решениям (2 минуты).
После работы ученики выполненные задания по карточкам с правильными решениями (решения выдаются учителем каждому ученику):
Решение варианта А1, Б1, В1 самостоятельной работы
Решение варианта А2, Б2, В2 самостоятельной работы
К самостоятельной работе прилагаются карточки с дополнительными заданиями, рассчитанные на более сильных учеников, за которые выставляется отдельная оценка "4" или "5".
Дополнительные задания для тех, кто справился с самостоятельной работой быстро.
VI. Подведение итогов. При выполнении самостоятельной работы учащийся набирает:
| Оценка | Вариант А | Вариант Б | Вариант В |
| «5» | 5 баллов | 10 баллов | 20 баллов |
| «4» | 4 балла | 8 баллов | 16 баллов |
| «3» | 3 балла | 6 баллов | 12 баллов |
| «2» | 2 балла | 4 балла | 8 баллов |
Задание на дом.
Если ученик выполнял вариант А, то №233, 235 (5, 6).
Если ученик выполнял вариант Б, то № 238(2,4), 239(2, 4).
Если ученик выполнял вариант В, то № 242.
Кроме того, ученики повторяют вопросы темы, по которым они допустили ошибки.
Дополнительное задание.
№1. Две автомашины (автомобиль с двигателем внутреннего сгорания1 автомобиль; автомобиль, работающий на газовом топливе2 автомобиль) одновременно выехали в направлении пункта А. По условию эксперимента, они должны были прекратить движение при показателе счетчика загрязнения, равном 72 г вредных веществ, содержащихся в выхлопных газах. Второй автомобиль проехал больше 1 автомобиля на 4 км (коэффициент загрязнения у него больше на 0,25). Вычислите коэффициент загрязнения для 1 и 2 автомобилей (отношение количества вредных веществ, выбрасываемых автомобилем за 1 км пути). Какой из автомобилей более экологически чистый?
Решение:
Пусть х% кислорода содержит первое вещество, тогда (х+15)% кислорода содержит второе вещество. Масса первого вещества 500/х млн. т, масса второго400/(х+15) млн. т. По условию задачи сказано, что масса двух веществ составляет 500/х+400/(х+15) или 30 млн. т. Составим уравнением.
500 + 400 =30
х х+15
30х²+450х+7500=0
х(х+15)
30х²+450х+7500=0,
х(х+15)0;
х²15х250=0,
х(х+15)0; х²15х250=0, по теореме, обратной теореме Виета
х1+х2=15, х1=10,
х1х2=250; х2=25;
х=10, х=25,
или
х(х+15)0 верно; х(х+15)0 верно;
х=10 не удовлетворяет условию задачи.
Ответ: первое вещество содержит 25% кислорода.
№2. Заводом выбрасываются загрязняющие вещества, в составе которых 18 кг SO2 и пыль. После того, как усовершенствовали фильтр, пыли в составе вещества стало меньше на 12 кг, после чего содержание пыли уменьшилось на 40%. Сколько загрязняющего вещества выбрасывалось первоначально?
№3. Колорадский жук наносит большой урон сельскому хозяйству, т.к. его плодовитость колоссальна. В среднем одна самка откладывает до 500 яиц. В благоприятный летний сезон количество жуков приближённо можно определить по формуле 500(х25)², а в неблагоприятный 300(х25) (период развития жука из яйца составляет примерно 25 дней). Опишите закон, по которому определяется количество жуков (включая самку) произведённых одной самкой, если в летнем сезоне благоприятных и неблагоприятных дней было примерно поровну. Постройте график. Сделайте практические выводы.
Решение: первоначально выбрасывалось 30 кг загрязняющего вещества.
Литература:
1. Алгебра и начала анализа. 11 класс: Учеб. для общеобразоват. учреждений/[Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачёва, Н.Е. Фёдорова и М.И. Шабунин]. – М.: Мнемозина, 2002.- 240c.: ил. – ISBN 5-346-00059-3..
2. Ершова А.П. Самостоятельные и контрольные работы по алгебре и началам анализа для 10-11 классов.[А.П.Ершова, В.В. Голобородько]. – М.: Илекса, 2005.
3. Изучение сложных тем курса алгебры в средней школе: Учебно-методические материалы по математике/ под ред. Л.Я.Фальке. – М.: Народное образование; Илекса; Ставрополь: Сервисшкола, 2004.
4. Ивлев Б.М. и др. Дидактические материалы по алгебре и началам анализа для 11 класса./ [Б.М. Ивлев, С.М. Саакян, С.И. Шварцбурд]. – М.: Просвещение, 2003. – 192 c.: ил. – ISBN 5-09-011832-9.
5 Лысенко Ф.Ф. Математика. Учебно-тренировочные тесты – 2006, [Текст]. / [Ф.Ф.Лысенко, В.Ю. Калашников, А.Б. Неймарк, О.Е. Кудрявцев и др.]; Ростов-на Дону; Легион, 2005. – 176 с. – ISBN 5-902806-15-1.


 Получите свидетельство
Получите свидетельство Вход
Вход












 Конспект урока по математике по теме "Решение иррациональных уравнений" (0.15 MB)
Конспект урока по математике по теме "Решение иррациональных уравнений" (0.15 MB)
 0
0 579
579 83
83 Нравится
0
Нравится
0


