Конспект и презентация к интегрированному уроку математики и информатики "Системы неравенств с двумя переменными"

Пояснительная записка

Цель урока:

 Научить применять знания и умения составления программ с использованием операторов ветвления, получаемые на уроках информатики, при выполнении заданий алгебры.

Задачи:

Обучающие:

научиться применять и объединять знания из различных общеобразовательных предметов для решения задач по алгебре и информатике;

закрепить понятие системы неравенств с двумя переменными;

закрепить алгоритм решения систем неравенств с двумя переменными;

научиться применять алгоритм решения заданий на определения условия принадлежности точки выделенному множеству;

разработать программу на языке Паскаль с использованием оператора ветвления и логических операций.

Развивающие:

развитие логического и абстрактного мышления;

развивать «критическое» мышление и интерес к предмету у учащихся в процессе решения проблемных ситуаций и заданий творческого характера;

развитие внимания.

Воспитывающие:

умение работать в коллективе;

оказывать взаимопомощь и контроль.

Тип урока: урок формирования умений и навыков.

Место проведения: компьютерный класс.

Оборудование: доска, маркер, компьютеры, проектор.

Необходимые знания и навыки: учитель и обучающиеся 9 класса должны владеть основами программирования. Либо же урок может быть проведён совместно учителями математики и информатики.

Ход урока:

1. Организационный момент.

Вступительное слово учителя. План урока, цель.

 - Сегодня мы продолжим изучение темы «Системы неравенств с двумя переменными». Но сначала повторим, как вы усвоили материал прошлого урока.

2. Устная работа учащихся с использованием проектора.

1) Демонстрируются задания на слайдах (слайды 2 - 6);

 2) Повторение алгоритма решения систем неравенств с двумя переменными (слайд 7).

 - Каков же алгоритм решения систем неравенств?( Выслушать учеников)

Ученики повторяют алгоритм решения систем неравенств:

Если одно из неравенств системы представлено в виде у >f(x), то это неравенство задает на плоскости область, которая лежит не ниже графика.

Если одно из неравенств системы представлено в виде у ?f(x), то это неравенство задает на плоскости область, которая лежит не выше графика.

 - Если линия f(x;у) - замкнутая, например окружность, или замкнутая ломанная?

Учащиеся предлагают следующее правило:

Если f(x;у)=0 - замкнутая линия, то неравенство f(x;у)>0, задает область лежащую вне замкнутой линии, а неравенство f(x;у)<0 - область лежащую внутри.

 3) Повторение правила пробной точки (слайд 8).

И наиболее универсальное, полезное для проверки правило - «Правило пробной точки»:

 Построить F(x;y) = 0 и G(x;y) = 0. Взяв из каждой области пробную точку,

 установить, являются ли ее координаты решением системы. Объединение

 полученных областей - решение системы неравенств.

  3. Применение навыков решения систем неравенств с двумя переменными при решении задания из задачника по информатике.

 Предлагается решить задачу №1 (Слайд 9):

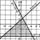
 Точка А задана координатами X, Y. Написать программу, которая выводит слово «Принадлежит», если точка принадлежит заштрихованной области (см. рисунок ) и «Не принадлежит» в противном случае.

Протестировать программу для точек (2. 5, 2), (1, 0), (0, 0), (0, - 2), ( - 1, - 1).

А) Учитель проводит фронтальный опрос - задаёт наводящие вопросы для начала решения задачи:

запись уравнения прямой через две точки;

запись уравнения прямой параллельной оси ОХ;

запись уравнения прямой параллельной оси ОУ.

Учащиеся отвечают.

Б) Один ученик решает у доски – находит уравнения ограничивающих заштрихованную фигуру прямых и записывает систему неравенств.

В) Составляется программа на Паскале (на слайде 10 опорные термины языка Паскаль)

Г) Набор учащимися программы на компьютере и проверка тестированием.

Весь материал – смотрите документ.