Основные цели: формировать понятие центральной симметрии, тренировать способность к построению симметричных точек и фигур.
Оборудование:
- проектор
- папки для наглядной геометрии с набором чертежных принадлежностей
-лист нелинованной бумаги (половинка А4)
- калька
-кнопка для прикалывания кальки
Актуализация.
- Что мы изучали на последних уроках? (Симметрию).
- Какие виды симметрии мы рассмотрели? (Осевую и поворотную).
- Какими свойствами обладают симметричные фигуры? (Равны)
- Сегодня мы рассмотрим еще один вид симметрии. Но сначала немного повторим.
2. Устные упраженения
1. Длина отрезка MО равна 6,5 см. Чему равна длина отрезка M1О1 симметричного отрезку MО относительно прямой b. (6,5см)
- Каким свойством симметричных фигур вы воспользовались? (Симметричные фигуры равны).
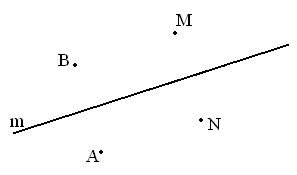
2. Является ли прямая m осью симметрии точек А и В? M и N? А и M? (В первых двух случаях да, а в третьем - нет).
3. Согните произвольно лист бумаги, разверните и проведите карандашом по линии сгиба. Отметьте на прямой точки С и О. Постройте точку С1 симметричную точке С относительно точки О. (30 с. обсуждают варианты решения в парах)
Постановка цели деятельности.
- Каким видом симметрии мы сегодня будем заниматься? (Симметрией относительно точки).
- Такую симметрию называют центральной симметрией.
- Сформулируйте цель урока. (Выяснить, что такое центральная симметрия)
- Сформулируйте тему урока. (Центральная симметрия).
Формирование представления о центральной симметрии.
-Вернемся к построению симметричной точки. Проведите половину дуги окружности с центром в точке О и радиусом СО. Точка пересечения дуги окружности и прямой а и есть искомая симметричная точка С1.
-Рассмотрите внимательно полученную модель. Еще раз мысленно проделайте все действия.
-Центральную симметрию иногда называют поворотной симметрией. Как вы думаете, почему? (обсуждаются варианты ответа)
- На какой угол осуществляется поворот и вокруг какой точки? ( 180о, вокруг точки О).
-Проведите в тетради прямую р, отметьте на ней точки Е и К. Постойте точку К1 симметричную точке К относительно точки Е. Придумайте название для точки Е.
-Расскажите соседу по парте как вы выполняли построение.
-Точка Е называется центром симметрии.
Исследование свойств точек, симметричных относительно точки.
-Вернемся снова к точкам С, О и С1. Что вы можете сказать о длинах отрезков ОС и ОС1? (они равны как радиусы окружности)
-Давайте убедимся в этом, измерив отрезки ОС и ОС1.
Запишите ОС=ОС1. Отметьте равные отрезки.
- Отметьте точку М на прямой а. Постройте ей симметричную точку М1 относительно точки О, не используя циркуль. (Дети обязательно догадаются, что она будет равноудалена от точки О, т.е МО=ОМ1). Сформулируйте правило построения точки симметричной данной.
- Что вы можете сказать о длинах отрезков МО и ММ1? (ММ1 в два раза длиннее МО).
Построение центра симметрии.
- Отметьте на обратной стороне листа точки Т и Т1. Известно, что они симметричны относительно точки А. Постройте точку А. (Дети измеряют расстояние ТТ1, могут соединить точки по линейке и находят его середину. Отмечают точку А).
- Выпишите равные отрезки. (АТ=АТ1)
-Сформулируйте правило построения центра симметрии.
7. Построение фигуры, симметричной относительно точки.
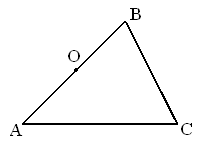
Постройте в тетради произвольный остроугольный треугольник АВС. Постройте треугольник А1В1С1 симметричный треугольнику АВС относительно точки О, где О – середина АВ.
Задание у некоторых или у всех вызовет затруднение.
- Наложите на ваш треугольник кальку и обведите его. Закрепите кальку в точке О кнопкой и поверните кальку на некоторый угол.
- Что произошло?
- При симметрии относительно точки, на какой угол производим поворот? (На 180 градусов). Поверните кальку на 180о.
- В какие точки перешли точки А, В и С? (В, А и С1)
- В какую точку перешла точка О? (О) Как она называется? (Центр симметрии).
- Как назвать фигуры АВС и АВС1? (Симметричные относительно точки).
-Такие фигуры называются центрально-симметричными.
8. Закрепление.
-Проверьте с помощью кальки, обладают ли фигуры симметрией относительно точки О.
9. Рефлексия.
- Что мы сегодня повторили?
- Что нового вы узнали на уроке?
- Проанализируйте свою работу на уроке.

 Получите свидетельство
Получите свидетельство Вход
Вход



















 Конспект факультативного занятия по теме "Центральная симметрия" (46.5 КB)
Конспект факультативного занятия по теме "Центральная симметрия" (46.5 КB)
 0
0 553
553 14
14 Нравится
0
Нравится
0


