|
| МИНИСТЕРСТВО ОБЩЕГО И ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ СВЕРДЛОВСКОЙ ОБЛАСТИ ГАПОУ СО «ОБЛАСТНОЙ ТЕХНИКУМ ДИЗАЙНА И СЕРВИСА» |
|
Утверждаю: Директор ОТД и С _________________/_С.Г. Голыгин/ «__25__»_____сентября___________2018 ____ г. |
КОМПЛЕКТ ОЦЕНОЧНЫХ СРЕДСТВ
ДЛЯ ПРОВЕДЕНИЯ ПРОМЕЖУТОЧНОЙ АТТЕСТАЦИИ
ПО УЧЕБНОЙ ДИСЦИПЛИНЕ
УОД.04 МАТЕМАТИКА
ППРС: 42.02.01 «Реклама»
Екатеринбург, 2018 г
КОС по учебной дисциплине «Математика» разработан на основе требований ФГОС среднего общего образования (Приказ Минобрнауки России от 17 мая 2012 г. № 413), рабочей программы общеобразовательной учебной дисциплины «Математика», составленной на базе программы для профессиональных образовательных организаций, рекомендованной Федеральным государственным автономным учреждением «Федеральный институт развития образования» (ФГАУ «ФИРО») в качестве примерной программы для реализации основной профессиональной образовательной программы СПО на базе основного общего образования с получением среднего общего образования (Протокол № 3 от 21 июля 2015 г. Регистрационный номер рецензии 375 от 23 июля 2015 г. ФГАУ «ФИРО»), в соответствии с ФГОС СПО по специальности 42.02.01 «Реклама» (Приказ Минобрнауки России от 12 мая 2014 г. № 510)
Разработчики:
Антонюк. Елена Владимировна, преподаватель ВКК
Правообладатель программы:
ГАПОУ СО «Областной техникум дизайна и сервиса» г. Екатеринбург
Рабочая программа рассмотрена и рекомендована на заседании методического совета ГАПОУ СО «Областной техникум дизайна и сервиса», г. Екатеринбург
Протокол методического совета № от « 25.09 » 2018 г.
Председатель методического совета Ю.С. Соловьянова
Комплект оценочных средств предназначен для оценки результатов освоения ОУД.04 математика
Таблица 1
| Результаты освоения (объекты оценивания)
| Основные показатели оценки результата и их критерии | Тип задания; № задания
| Форма аттестации (в соответствии с учебным планом) |
| В результате освоения дисциплины обучающийся знает: Значение математической науки для решения задач, возникающих в науке и практике; широту и то же время ограниченность применения математи -ческих методов к анализу и исследованию процессов и явлений в природе и обществе; Формирование и развитие математической науки, историю развития понятия числа, создания математического анализа, возникновения и развития геометрии; Универсальный характер законов логики математи -ческих рассуждений, их применение во всех областях человеческой деятельности; Вероятностный характер различных процессов окружающего мира; умеет: Выполнять вычисления и преобразованиявыполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма; вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, тригонометрические и логарифмы; Умеет решать уравнения и неравенства: -решать рациональные и иррациональные, показательные, логарифмические, тригонометрические уравнения и их системы; - решать уравнения простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений графический метод; - решать рациональные, показательные, логарифмические неравенства; Умеет выполнять действия с функциями: - определять значение функции по значению аргумента при различных способах задания функции; Описывать по графику поведение функции, ее свойства и находить наибольшие и наименьшие значения функции, строить графики изученных функций; - вычислять производные и первообразные элементарных функций; - исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функции; Умеет выполнять действия с геометрическими фигурами, координатами и векторами: - решать планиметрические задачи на нахождение геометрических величин (углов, длин, площадей); - решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); используя планиметрические факты и методы; - определять координаты точки; Умеет строить и исследовать простейшие математические модели: - моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры; - моделировать реальные ситуации на языке геометрии и исследовать построенные модели с использованием геометрических понятий, теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин; - проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения. • Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни: - анализировать реальные числовые данные; осуществлять практические расчеты по формулам, пользоваться оценкой и прикидкой при практических расчетах; - описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках; - решать прикладные задачи, в том числе физического и социально- экономического характера, на наибольшие и наименьшие значения. На нахождение скорости и ускорения. | Знание значения математической науки для решения задач, возникающих в науке и практике; широту и то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе; Знание формирования и развития математической науки, историю развития понятия числа, создания математического анализа, возникновения и развития геометрии; Знание универсального характера законов логики математических рассуждений, их применение во всех областях человеческой деятельности; Знание вероятностного характера различных процессов окружающего мира; Умение выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма; Умение вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, тригонометрические и логарифмы; • Умение решать рациональные и иррациональные, показательные, логарифмические, тригонометрические уравнения и их системы; - решать уравнения простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений графический метод; - решать рациональные, показательные, логарифмические неравенства;
• Умение определять значение функции по значению аргумента при различных способах задания функции; Описывать по графику поведение функции, ее свойства и находить значения функции, строить графики изученных функций; - вычислять производные и первообразные элементарных функций; - исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функции; • Умение решать планиметрические задачи на нахождение геометрических величин (углов, длин, площадей); - решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); используя планиметрические факты и методы; - определять координаты точки;
• Умение моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры; - моделировать реальные ситуации на языке геометрии и исследовать построенные модели с использованием геометрических понятий, теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин; • Умение проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения. • Умение анализировать реальные числовые данные; осуществлять практические расчеты по формулам, пользоваться оценкой и прикидкой при практических расчетах; - описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках; - решать прикладные задачи, в том числе физического и социально- экономического характера, на наибольшие и наименьшие значения. на нахождение скорости и ускорения.
| Письменные дифференциро- ванные задания обязательного и дополнительного уровней | экзамен |
2. Комплект оценочных средств
2.1. Промежуточная аттестация
Формой промежуточной аттестации по учебной дисциплине «Математика» является письменный экзамен. Итогом экзамена является оценка, выраженная в баллах по 5-ти бальной шкале оценки.
I. ПАСПОРТ
Назначение:
Комплект контрольно-оценочных материалов (КОМ) промежуточной аттестации предназначен для контроля и оценки результатов освоения обучающимися учебной дисциплины «Математика» по итогам 1-го курса по специальности СПО
ППРС: 42.02.01 Реклама
II. ЗАДАНИЕ ДЛЯ ОБУЧАЮЩЕГОСЯ
Инструкция
На выполнение письменной экзаменационной работы по математике дается 5 астрономических часов (300 минут). Экзаменационная работа содержит по три задания из шести основных разделов курса, различного уровня сложности. Экзаменационная работа состоит из двух частей: обязательной и дополнительной.
Обязательная часть содержит задания минимального обязательного уровня А и Б. Дополнительная часть содержит более сложные задания под буквой В. При выполнении заданий требуется представить ход решения и указать полученный ответ. Если приводится неверный ответ или решение отсутствует, то ставится 0 баллов.
Баллы, полученные за все выполненные задания, суммируются.
Постарайтесь правильно выполнить как можно больше заданий и набрать наибольшее количество баллов.
Перед началом работы внимательно изучите критерии оценивания работы.
КРИТЕРИИ ОЦЕНИВАНИЯ РАБОТЫ
| Оценка Задание А- 0,5 баллов Задание Б- 1 балл Задание В- 1,5 балла | Число баллов, необходимое для получения оценки |
| «3» (удовлетворительно) | 3 - 5,5 баллов |
| «4» ( хорошо) | 6 – 8,5 баллов |
| «5» (отлично) | 9 и более баллов |
| «2» (неудовлетворительно) | Менее 2,5 баллов |
Начинать выполнение работы следует с решения заданий обязательного уровня - А и Б. Для получения положительной оценки «3» необходимо выполнить не менее 6 заданий обязательного уровня.
Только после того, как Вы наберете необходимое количество для удовлетворительной оценки, можно переходить к решению остальных заданий. Для получения оценки «4» необходимо выполнение не менее 10 заданий. При выполнении всех заданий обязательного уровня и не менее трех заданий дополнительного уровня В выставляется оценка «5».
Желаем успехов!
Билет 1
1.Показательная функция
А) вычислить 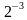 :
: 
 +
+ 
Б) решить неравенство 
В) решить уравнение: 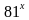 -2 ·
-2 · -3 =0
-3 =0
2. Логарифмическая функция
А) вычислить 
Б) решить уравнение: 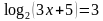
В) решить неравенство: 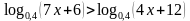
3. Тригонометрические функции
А) решить уравнение: cos2x = -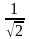
Б) вычислить cosx, если sinx = -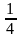 , п
, п
В) упростить выражение tg(П –x) · cos (2П + х)
Sin( 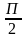 + x ) · ctg (
+ x ) · ctg (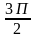 - x)
- x)
4. Производная и ее применение
А) Найти мгновенную скорость движения точки в момент времени t =2 сек., если закон ее движения: s(t) = 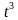 -2,5
-2,5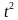 -5
-5
Б) Найти экстремумы функции f(x) = 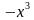 +3
+3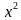 -4
-4
В) Найти наименьшее и наибольшее значения функции у(х) =2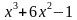 на отрезке
на отрезке 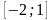
5. Интеграл и его применение
А) найти первообразную функции f(x) = 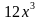 - 9
- 9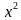 +4x -5cosx
+4x -5cosx
Б) вычислить:  dx
dx
В) найти площадь фигуры, ограниченной линиями: у = +1, у = 0, х = 0, х = 2
6. Геометрия
А) Сторона АС прямоугольного треугольника АВС равна 16 см. Угол при вершине В прямой, . Найдите длину стороны ВС.
Б) Сторона основания правильной треугольной призмы равна 12 см. Диагональ боковой грани равна 15 см. Найдите объем призмы.
В) Площадь основания цилиндра равна 36 , а площадь осевого сечения равна 240
. Найдите площадь боковой поверхности цилиндра.
Билет 2
1.Показательная функция
А) вычислить ·
+
Б) решить неравенство 625
В) решить уравнение: -3 ·
-4 =0
2. Логарифмическая функция
А) вычислить
Б) решить уравнение:
В) решить неравенство:
3. Тригонометрические функции
А) решить уравнение: sin6x = -
Б) вычислить sinx , если cosx = , 0
В) упростить выражение cos(2П –x) · tg (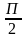 + х)
+ х)
Sin( 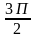 + x ) · ctg (П - x)
+ x ) · ctg (П - x)
4. Производная и ее применение
А) Найти мгновенную скорость движения точки в момент времени t =1 сек., если закон ее движения: s(t) = - 2
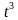 - t
- t
Б) Найти экстремумы функции f(x) = - 4
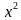 +2
+2
В) найти наименьшее и наибольшее значения функции у(х) =2 на отрезке
5. Интеграл и его применение
А) Найти первообразную функции: f(x) = - 6
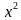 +3
+3 -7sinx
Б) вычислить: dx
В) найти площадь фигуры, ограниченной линиями: у = 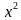 +5, у = 0, х = -1, х = 1
+5, у = 0, х = -1, х = 1
6. . Геометрия
А) Сторона КМ прямоугольного треугольника DKM равна 6 см. Угол К прямой, а при вершине М равен 60 Найдите длину стороны DK.
Б) Высота правильной четырехугольной призмы равна 5 см. Диагональ боковой грани равна 7 см. Найдите объем призмы.
В) Площадь основания конуса равна 25 , а площадь осевого сечения равна 40
. Найдите площадь боковой поверхности конуса.
Билет 3
1.Показательная функция
А) вычислить
+
Б) решить неравенство
В) решить уравнение:  -4 ·
-4 · +3 =0
2. Логарифмическая функция
А) вычислить
Б) решить уравнение:
В) решить неравенство:
3. Тригонометрические функции
А) решить уравнение: ctg 6x = -
Б) вычислить cos х, если sinx = - ,
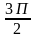
В) упростить выражение ctg (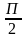 –x) · sin (2П - х)
–x) · sin (2П - х)
Sin( 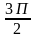 - x ) · ctg (
- x ) · ctg (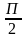 + x)
+ x)
4. Производная и ее применение
А) Найти мгновенную скорость движения точки в момент времени t =4 сек., если закон ее движения: s(t) =4 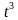 - 5
- 5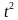 + t
+ t
Б) Найти экстремумы функции f(x) = 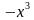 +12x - 1
+12x - 1
В) найти наименьшее и наибольшее значения функции у(х) =2 на отрезке
5. Интеграл и его применение
А) Найти первообразную функции : f(x) = - 6
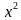 + 2x - 3
+ 2x - 3
Б) вычислить: dx
В) найти площадь фигуры, ограниченной линиями: у = -1, у = 0, х = 1, х = 2
6. Геометрия
А) Сторона ЕР прямоугольного треугольника ЕРТ равна 14 см. Угол Р прямой, а при вершине Е равен 60 Найдите длину стороны ТР.
Б) Стороны основания АВ и АС, прямой треугольной призмы АВСА1В1С1, соответственно равны 3 и 5 см, . Высота призмы равна 10 см. Найдите объем призмы.
В) Площадь основания цилиндра равна 6 , а площадь осевого сечения равна 160
. Найдите площадь боковой поверхности цилиндра.
Билет 4
1.Показательная функция
А) вычислить ·
+
Б) решить неравенство 25
В) решить уравнение +4 ·
-5 =0
2. Логарифмическая функция
А) вычислить
Б) решить уравнение:
В) решить неравенство:
3. Тригонометрические функции
А) решить уравнение sin10x =
Б)вычислить sinx, если cos x = и 0x
В) упростить выражение tg(2П –x) · cos (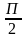 - х)
- х)
cos( 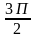 + x ) · ctg (П + x)
+ x ) · ctg (П + x)
4. Производная и ее применение
А) Найти мгновенную скорость движения точки в момент времени t =3 сек., если закон ее движения: s(х) = 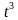 - 3
- 3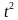 +4
+4
Б) Найти экстремумы функции f(x) = - 2
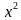 +1
+1
В) найти наименьшее и наибольшее значения функции у(х) =2 на отрезке
5. Интеграл и его применение
А) Найти первообразную функции f(x) = - 27
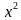 +13
+13 +7sinx
Б) вычислить: dx
В) найти площадь фигуры, ограниченной линиями: у =4- 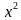 , у = 0, х = 1, х = 2
, у = 0, х = 1, х = 2
6. Геометрия
А) Сторона АК прямоугольного треугольника АВК равна 10 см. Угол при вершине В прямой. Найдите длину стороны ВК, если .
Б) Высота четырехугольной призмы равна 8 см. Диагональ основания равна 10 см, а одна из сторон основания 6 см.. Найдите объем призмы.
В) Площадь основания конуса равна , а площадь осевого сечения равна 32
. Найдите площадь боковой поверхности конуса.
| ПАКЕТ ЭКЗАМЕНАТОРА ФИО студента (заполняется вручную для каждого студента)___________________________________________________________ | |||
| Билет № задания (А, Б, В)________ Выполнение практического задания _________________________________ указывается тип задания (теоретическое, практическое), номер задания и его краткое содержание Каждый критерий оценивается в два балла 0- не проявлен 1- частично проявлен 2- проявлен | |||
| Результаты освоения (объекты оценки) - Знает формулы для преобразования степеней, радикалов, логарифмов - Знает методы решения показательных, логарифмических уравнений - Знает формулы тригонометрии | Критерии оценки результата Рейтинговая система оценивания «5» 44-64 баллов «4» 32-42 баллов «3» 18-30 баллов «2» 17 и менее баллов | Отметка о выполнении
| |
| - Знает приемы преобразования тригонометрических выражений - Знает формулы и правила дифференцирования - Знает прием вычисления значения производной функции в точке - Знает алгоритм нахождения наименьшего и наибольшего значений функции на отрезке - Знает схему исследования функции с помощью производной для построения графика - Знает формулы и правила интегрирования - Знает приемы вычисления площадей фигур с помощью интеграла | |
| |
| -Умеет применять формулы преобразования степеней, радикалов, логарифмов - Применяет методы решения показательных, логарифмических уравнений - Использует формулы тригонометрии - Владеет приемами преобразования тригонометрических выражений - Применяет методы решения тригонометрических уравнений -Применяет формулы и правила дифференцирования - Вычисляет значение производной функции в точке | |||
| - Применяет алгоритм нахождения наименьшего и наибольшего значений функции на отрезке | |||
| - Исследует функции с помощью производной для построения графика | |||
| - Использует формулы и правила интегрирования
| |||
| - Владеет приемами вычисления площадей фигур с помощью интеграла
| |||
| Условия выполнения заданий Оборудование: справочные материалы | |||
ФИО обучающегося и дата проведения
Подписи экзаменаторов: Ведущий преподаватель__________________________(___________________)
Зам. по УР______________________________________(_________________)
2.3 Эталоны ответов
Билет 1
а) 0 б) х-1 в)0,5
а) 1 б) 1 в)х2
а) x = +
б) -
в) -1
а) 2 б) х=2 максимум, х= 0 минимум в)
а) F(x) = 3 +2
б)131
в)6
а) 4 б) 324
в) 240
Билет 2
а) 73 б) х в)2
а) 1 б) 2 в) x 5
а) x = +
б)
в) -1
а) 5 б) х= 1 минимум, х=0 максимум в)
а) F(x) = 4 б) 18 в)10
а) 6
б) 245
в) 5
Билет 3
а) 4 б) х в) x = 0, x = 1
а)1 б)5,8 в) (
а) x = +
б)
а) 9 б) х=2 максимум, х= -2 минимум в)
а) F(x) = 2 б)10 в)2,75 кв.ед.
а) 2
б) 60
в) 160
Билет 4
а) 33 б) х-1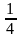 в) 0
в) 0
а) 2 б) 5 в) х
а) x = +
б) -
в) -1
а) 15 б) х= 0 максимум, х = 1 минимум в)
а) F(x) = 6 б) 57 в)1 кв. ед.
а)5
б) 384
в)
ГАПОУ СО «Областной техникум дизайна и сервиса»
Лист оценивания знаний и умений обучающихся
в промежуточной аттестации по учебной дисциплине «МАТЕМАТИКА»
Специальность Группа Преподаватель: Антонюк Е.В.
| 0- не проявлен 1- частично проявлен 2- проявлен «5» 44-64 баллов «4» 32-42 баллов «3» 18-30 баллов «2» 17 и менее баллов | Ф.И.О. обучающихся | ||||||||||||||||||||
| | | | | | | | | | | | | | | | | | | | | | |
| ЗАДАНИЕ А (практическое) | |||||||||||||||||||||
| ЗНАНИЯ: | | | | | | | | | | | | | | | | | | | | | |
| 1.Знает ограниченный набор формул для преобразования степеней, радикалов. логарифмов | | | | | | | | | | | | | | | | | | | | | |
| 2.Знает простейшие методы решения показательных, логарифмических, тригонометрических уравнений | | | | | | | | | | | | | | | | | | | | | |
| 3.Знает ограниченный набор формул и правил дифференцирования | | | | | | | | | | | | | | | | | | | | | |
| 4.Знает прием вычисления значения производной функции в точке | | | | | | | | | | | | | | | | | | | | | |
| 5.Знает ограниченный набор формул и правил интегрирования 6.Знает формулу Ньютона-Лейбница для вычисления интеграла | | | | | | | | | | | | | | | | | | | | | |
| ЗАДАНИЕ Б (практическое) № 2 | |||||||||||||||||||||
| 1. Знает формулы преобразования степеней, радикалов. логарифмов | | | | | | | | | | | | | | | | | | | | | |
| 2. Знает методы решения показательных, логарифмических уравнений | | | | | | | | | | | | | | | | | | | | | |
| 3.Знает формулы тригонометрии 4. Знает приемы преобразования тригонометрических выражений 5. Знает формулы и правила дифференцирования | | | | | | | | | | | | | | | | | | | | | |
| 6.Знает алгоритм нахождения наименьшего и наибольшего значений функции на отрезке 8.Знает приемы вычисления площади криволинейной трапеции с помощью интеграла | | | | | | | | | | | | | | | | | | | | | |
| ЗАДАНИЕ В (практическое) | |||||||||||||||||||||
| 3. Знает формулы тригонометрии 8. Знает формулы и правила интегрирования УМЕНИЯ: | | | | | | | | | | | | | | | | | | | | | |
| ЗАДАНИЕ А (практическое) | |||||||||||||||||||||
| 2. Применяет простейшие методы решения показательных, логарифмических, тригонометрических уравнений 3. Владеет ограниченным набором формул и правил дифференцирования 4. Вычисляет значение производной функции в точке 5. Владеет ограниченным набором формул и правил интегрирования 6.Вычисляет простейший интеграл по формуле Ньютона-Лейбница | | | | | | | | | | | | | | | | | | | | | |
| ЗАДАНИЕ Б практическое) | |||||||||||||||||||||
| 1. Применяет формулы преобразования степеней, радикалов, логарифмов 4. Владеет приемами преобразования тригонометрических выражений 6. Применяет алгоритм нахождения наименьшего и наибольшего значений функции на отрезке 7.Применяет формулы и правила интегрирования
| | | | | | | | | | | | | | | | | | | | | |
| 8.Владеет приемами вычисления площади криволинейной трапеции с помощью интеграла | | | | | | | | | | | | | | | | | | | | | |
| ЗАДАНИЕ В практическое) | |||||||||||||||||||||
| 1. Применяет формулы преобразования степеней, радикалов. логарифмов | | | | | | | | | | | | | | | | | | | | | |
| 2. Владеет приемами решения показательных, логарифмических неравенств 3. Использует формулы тригонометрии 4. Владеет приемами преобразования тригонометрических выражений 5. Применяет методы решения тригонометрических уравнений 6. Использует формулы и правила дифференцирования 7. Исследует функции с помощью производной для построения графика 8. Использует формулы и правила интегрирования 9.Владеет приемами вычисления площадей фигур с помощью интеграла | | | | | | | | | | | | | | | | | | | | | |
| Количественная оценка | | | | | | | | | | | | | | | | | | | | | |
| Дискрептивная оценка | | | | | | | | | | | | | | | | | | | | | |
Дата проведения экзамена___________________________________ Подпись преподавателя _______________________________________
13

 Получите свидетельство
Получите свидетельство Вход
Вход













 Комплект оценочных средств по математике для специальности 42.02.01 Реклама (189.83 KB)
Комплект оценочных средств по математике для специальности 42.02.01 Реклама (189.83 KB)
 0
0 170
170 4
4 Нравится
0
Нравится
0


