Итоговая контрольная работа по алгебре 9 класс в формате ОГЭ
Вариант 1
1. Найдите значение выражения 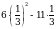
2. О числах a и c известно, что 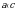 . Какое из следующих неравенств неверно?
. Какое из следующих неравенств неверно?
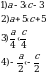
3. Найдите значение выражения 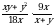 при x = −9,6, y = −0,4.
при x = −9,6, y = −0,4.
4. Найдите корни уравнения 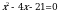
Если корней несколько, запишите их в ответ без пробелов в порядке возрастания.
5. На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 5 с рисом и 21 с повидлом. Андрей наугад выбирает один пирожок. Найдите вероятность того, что он окажется с повидлом.
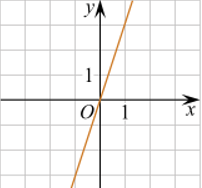
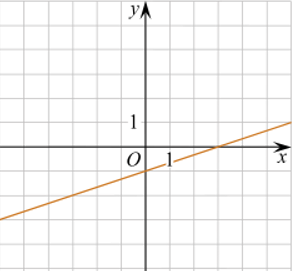
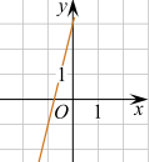
6. Установите соответствие между графиками функций и формулами, которые их задают.
Формулы
| 1) у=х+3 | 2) у=-3х | 3) у=3 | 4) у=3х |
Графики
| А) | Б) | В) |
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
|
7. Перевести значение температуры по шкале Цельсия в шкалу Фаренгейта позволяет формула F = 1,8C + 32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Цельсия соответствует 155° по шкале Фаренгейта? Ответ округлите до десятых.
8. Решите неравенство 
1)
2) нет решений
3)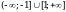
4)[-1;1]
9. В амфитеатре 14 рядов. В первом ряду 20 мест, а в каждом следующем на 3 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?
10. Сократите дробь
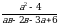
11. Из городов А и В навстречу друг другу одновременно выехали мотоциклист и велосипедист. Мотоциклист приехал в В на 48 минут раньше, чем велосипедист приехал в А, а встретились они через 18 минут после выезда. Сколько часов затратил на путь из В в А велосипедист?
Итоговая контрольная работа по алгебре 9 класс в формате ОГЭ
Вариант 2
1. Найдите значение выражения 
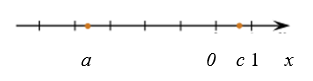
2. На координатной прямой отмечены числа а и с. Какое из следующих утверждений неверно?
В ответе укажите номер выбранного варианта.
1)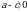
2)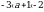
3)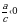
4)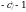
3. Упростите выражение 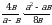 и найдите его значение при а=19, в=8,2. В ответе запишите найденное значение.
и найдите его значение при а=19, в=8,2. В ответе запишите найденное значение.
4. Решите уравнение 
5. На тарелке лежат одинаковые на вид пирожки: 4 с мясом, 8 с капустой и 3 с вишней. Петя наугад выбирает один пирожок. Найдите вероятность того, что он окажется с вишней.
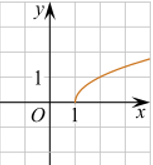
6. Установите соответствие между функциями и их графиками.
| 1) | 2) |
| 3) | 4)
|
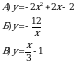
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
| А | Б | В |
|
|
| |
7. Зная длину своего шага, человек может приближенно подсчитать пройденное им расстояние s по формуле s = nl, где n — число шагов, l — длина шага. Какое расстояние прошел человек, если l = 80 см, n = 1600? Ответ выразите в километрах.
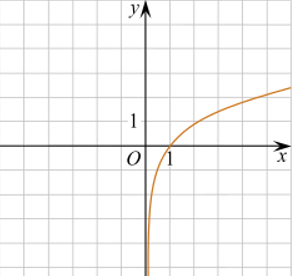
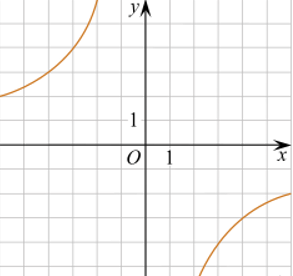
8. На каком рисунке изображено множество решений неравенства  ?
?
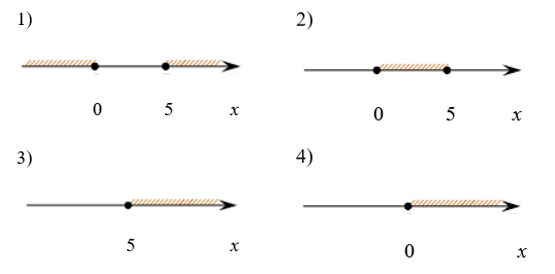
9. Бригада маляров красит забор длиной 150 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 75 метров забора. Определите, сколько дней бригада маляров красила весь забор.
10. Решите уравнение 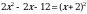
11. Первую половину пути автомобиль проехал со скоростью 42 км/ч, а вторую — со скоростью 48 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.
Итоговая контрольная работа по алгебре 9 класс в формате ОГЭ
Вариант 3
1. Найдите значение выражения 
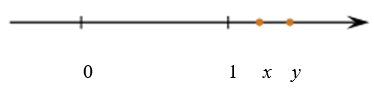
2. Числа x и y отмечены точками на координатной прямой. Расположите в порядке возрастания числа 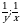 и 1.
и 1.
В ответе укажите номер правильного варианта.
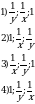
3. Упростите выражение  и найдите его значение при
и найдите его значение при 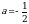 . В ответе запишите полученное число.
. В ответе запишите полученное число.
4. Решите уравнение 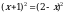
5. В магазине канцтоваров продается 200 ручек, из них 31 красная, 25 зеленых, 38 фиолетовых, еще есть синие и черные, их поровну. Найдите вероятность того, что при случайном выборе одной ручки будет выбрана красная или черная ручка.
6. Укажите соответствие между графиками функций и формулами, которые их задают.
| А) | Б) | В) |
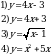
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
| А | Б | В |
|
|
|
|
7. Площадь четырехугольника можно вычислить по формуле  где d1 и d2 — длины диагоналей четырехугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если
где d1 и d2 — длины диагоналей четырехугольника, α — угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d2, если 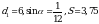
8. Решите неравенство 
В ответе укажите номер правильного варианта.
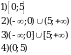
9. Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3700 рублей, а за каждый следующий метр — на 1700 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 8 метров?
10. Решите систему уравнений 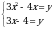
11. Два автомобиля одновременно отправляются в 240-километровый пробег. Первый едет со скоростью на 20 км/ч большей, чем второй, и прибывает к финишу на 1 ч раньше второго. Найдите скорость первого автомобиля.
В-1
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| -3 | 4 | -0,2 | -37 | 0,7 | 134 | 68,3 | 3 | 47 | (а+2)/(в-3) | 1,2 |
В-2
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 1 | 9,5 | -6 | 0,2 | 142 | 1,28 | 2 | 4 | 8; -2 | 44,8км/ч |
В-3
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 7 | 1 | 16 | 0,5 | 0,42 | 243 | 15 | 1 | 77200 | (1; -1) ;(4/3;0) | 80км/ч |
Итоговая контрольная работа по геометрии 9 класс в формате ОГЭ
Вариант 1
1. В треугольнике ABC угол C равен 90°, 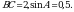 Найдите AB.
Найдите AB.
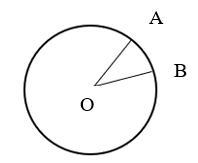
2. На окружности с центром O отмечены точки A и B так, что  .Длина меньшей дуги AB равна 63. Найдите длину большей дуги.
.Длина меньшей дуги AB равна 63. Найдите длину большей дуги.
3. В ромбе сторона равна 10, одна из диагоналей — 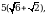 а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.
а угол, из которого выходит эта диагональ, равен 30°. Найдите площадь ромба.
4. На клетчатой бумаге с размером клетки 1х1 изображен прямоугольный треугольник. Найдите длину его большего катета.
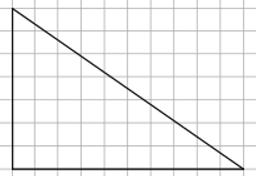
5. Какие из следующих утверждений верны?
1. Треугольника со сторонами 1, 2, 4 не существует.
2. Медиана треугольника делит пополам угол, из вершины которого проведена.
3. Все диаметры окружности равны между собой.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
6. В выпуклом четырехугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырехугольника NPQM можно описать окружность, PQ = 55, SQ = 1.
7. В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC = ED. Докажите, что данный параллелограмм — прямоугольник.
Итоговая контрольная работа по геометрии 9 класс в формате ОГЭ
Вариант 2
1. В треугольнике ABC известно, что АС=30, ВС=16, угол C равен 90°. Найдите радиус описанной окружности этого треугольника.
2. Радиус окружности, вписанной в трапецию, равен 16. Найдите высоту этой трапеции.

3. В трапеции ABCD известно, что AD=8, BC=7, а ее площадь равна 45. Найдите площадь треугольника ABC.

4. На клетчатой бумаге с размером клетки 1x1 изображена фигура. Найдите ее площадь.
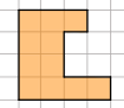
5. Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудаленная от концов отрезка.
2) Центром вписанной в треугольник окружности является точка пересечения его биссектрис.
3) Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и углу другого прямоугольного треугольника, то такие треугольники равны.
6. Основания трапеции равны 16 и 34. Найдите отрезок, соединяющий середины диагоналей трапеции.
7. В остроугольном треугольнике ABC проведены высоты АА1 и ВВ1. Докажите, что углы АА1В1 и АВВ1 равны.
Итоговая контрольная работа по геометрии 9 класс в формате ОГЭ
Вариант 3
1. В прямоугольном треугольнике ABC катет AC = 75, а высота CH, опущенная на гипотенузу, равна 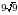 . Найдите
. Найдите 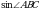
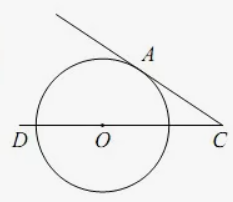
2. В угол C величиной 18° вписана окружность, которая касается сторон угла в точках A и B, точка O - центр окружности. Найдите угол AOB. Ответ дайте в градусах.

3. В трапеции ABCD известно, что AD = 5, BC = 1, а ее площадь равна 51. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.
4. На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите ее площадь.

5. Какое из следующих утверждений верно?
1. Вписанный угол, опирающийся на диаметр окружности, прямой.
2. Если три угла одного треугольника равны соответственно трем углам другого треугольника, то такие треугольники равны.
3. Отношение площадей подобных треугольников равно коэффициенту подобия.
В ответ запишите номер выбранного утверждения.
6. Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключенная внутри этого угла, равна 130°.
7. Биссектрисы углов C и D трапеции ABCD пересекаются в точке P, лежащей на стороне AB. Докажите, что точка P равноудалена от прямых BC, CD и AD.
В-1
| 1 | 2 | 3 | 4 | 5 | 6 |
| 4 | 747 | 50 | 10 | 13 | 3024 |
В-2
| 1 | 2 | 3 | 4 | 5 | 6 |
| 17 | 32 | 21 | 11 | 23 | 9 |
В-3
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0,08 | 162 | 17 | 35 | 1 | 40 |

 Получите свидетельство
Получите свидетельство Вход
Вход















 Итоговая контрольная по алгебре и по геометрии 9 класс в формате ОГЭ (342.22 KB)
Итоговая контрольная по алгебре и по геометрии 9 класс в формате ОГЭ (342.22 KB)
 0
0 1828
1828 75
75 Нравится
0
Нравится
0


