Использование личностно - ориентированных педагогических технологий в формировании ключевых компетенций

Использование личностно - ориентированных педагогических технологий в формировании ключевых компетенций

Мартынюк М. А.

 Наиболее продуктивной формой, способствующей формированию познавательных мотивов и математической компетентности, реализующей основные цели математического образования, я считаю, личностно-ориентированный  урок математики.

На мой взгляд, можно выделить следующие задачи личностно-ориентированного урока математики:

- личностный рост, развитие субъективности, саморазвитие студентов;

- интеллектуальное развитие студентов.  

К принципиальным основам, гарантирующим реализацию целей и задач всего познавательного процесса на личностно-ориентированном уроке математики, я считаю необходимым отнести:

- необходимость создания на уроке условий, способствующих заинтересованности студента в учении, саморазвитии;

- преподаватель – это только организатор и помощник учебно-познавательной деятельности студентов, а не главное действующее лицо на уроке;

   - организация учебного процесса через диалог или полилог;

   - свобода выбора студентом уровня  и темпа обучения.

= Если рассмотреть эту систему на примере урока математики по изучению нового материала, то можно выделить 5 основных этапов урока математики:

= 1 этап. Актуализация опорных знаний. На данном этапе главной задачей является включение каждого студента группы в работу на уроке, проведение дидактической игры «Я знаю, а ты?». Возможный вариант такой игры на одном из уроков геометрии вы можете видеть на экране.

= 2 этап.  Включение студентов в целеполагание. На данном этапе рационально использование заданий, вовлекающих студентов в реальные проблемные ситуации, решение которых определяет учебно-познавательные цели урока (например, при изучении темы «Первообразная функции» студентам предлагается объяснить значение слова первообразная. Значит, что же такое первообразная функции? (первый образ функции) Так чему же сегодня будет посвящён наш урок математики?).

=. 3 этап. Основной. Цель этого этапа – формирование самостоятельных умений, способность принимать решения.

= 4 этап. Этап контроля знаний студентов. На данном этапе вместо традиционной  оценки  знаний можно предлагать не совсем привычные задания, например, составить терминологический словарь урока геометрии на тему «Многогранники».

= 5 этап. Итог урока - рефлексия. Например, я не знал…, а теперь знаю…, у меня получилось… и др.

Личностно-ориентированный урок математики развивает способность размышлять, анализировать, что в будущем поможет самостоятельно принимать решения. В ходе учебных занятий я обращаю внимание на формирование трёх уровней математической компетентности: уровень воспроизведения, уровень установления связей, уровень рассуждений.

= Первый уровень (уровень воспроизведения) — это прямое применение в знакомой ситуации известных фактов, стандартных приемов, распознавание математических объектов и свойств, применение известных алгоритмов и технических навыков, работа со стандартными, знакомыми выражениями и формулами, непосредственное выполнение вычислений. Например, сюда можно отнести уроки по алгебре и началам анализа на темы: «Решение простейших тригонометрических уравнений», «Решение простейших тригонометрических неравенств» и другие.

Второй уровень (уровень установления связей) строится на репродуктивной деятельности по решению задач, которые, хотя и не являются типичными, но все же знакомы студентам или выходят за рамки известного лишь в очень малой степени. Обычно в этих задачах присутствует больше требований к интерпретации решения, они предполагают установление связей между разными представлениями ситуации, описанной в задаче, или установление связей между данными в условии задач. К данному уровню можно отнести практически любой урок по выработке умений и навыков по геометрии в разделе стереометрия.

Третий уровень (уровень рассуждений) строится как развитие предыдущего уровня. Для решения задач этого уровня требуются определенная интуиция, размышления и творчество в выборе математического инструментария, интегрирование знаний из разных разделов курса математики, самостоятельная разработка алгоритма действий. Уроки по стереометрии также очень помогают в формировании уровня рассуждений, так как требуют развития пространственных представлений об изучаемом теле и его основных свойствах.

Так как же при использовании личностно-ориентированных педагогических технологий на уроке математики сформировать ключевые компетенции?

Появление нового результата образования поставило преподавателя перед необходимостью использования различных видов личностно – ориентированных педагогических технологий, методов и приемов работы со студентами на уроке и во внеурочное время. Их вы можете видеть в данный момент на экране. Я остановлюсь более подробно на некоторых из них: =

1. метод направляющих текстов, который предполагает сообщение студентам с помощью словесно-знаковых средств информации сравнительно небольшого объёма для индивидуального восприятия, очень эффективен на уроках математики, так как помогает с помощью очень кратких записей путём символов и условных обозначений изучать разделы по предметам математического цикла, на которые отводится небольшое количество часов. Это в свою очередь позволит сэкономить время на изучении теории, а больше уделить времени формированию практических умений и навыков. Например, алгоритм решения неравенства методом интервалов.

2. проблемное и проектное обучение.

= Типы проблемных ситуаций, используемых мною на уроках математики:

• ситуация конфликта, например, когда при доказательстве теоремы методом от противного мы получаем противоречие;

• ситуация несоответствия, например, при изучении иррациональных уравнений можно предложить студентам проверить, является ли число 5 корнем рационального уравнения √х-6=√4-х (нет). А если бы нам нужно было бы решить это уравнение, то необходимо возведение обеих частей в квадрат, тогда х=5. Единственный способ решения приводит к корню, который является посторонним, что и приводит к внешнему несоответствию между фактами, а значит и проблемной ситуации в целом;

• ситуация предположения, например, на уроке геометрии, когда мы предполагаем, а затем уже доказываем подобие двух треугольников, а значит и отношение соответствующих сторон;

• ситуация выбора, например, при решении квадратного уравнения различными способами (через дискриминант, или по т. Виета) по выбору самого студента.

Примеры таких заданий вы сейчас видите на экране.

= На своих уроках математики я стараюсь формировать следующие компетенции:

• информационная, например,  при изучении новых терминов студенты, пользуясь толковым словарем, дают различные определения математического понятия: в математике модуль – это…, в строительстве модуль – это…,  в космонавтике модуль – это… и т.д.;

• коммуникативная, например, использование на уроках математических софизмов, таких как следующее удивительное «доказательство» равенства 1 = -1:

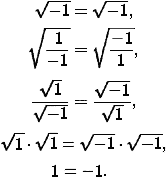
• готовность к самообразованию, саморазвитию, самосовершенствованию, например, студентам предлагается самим составить тест, найдя варианты ошибочных и правильных ответов.

= Как видно из всего выше сказанного, характерными признаками личностно-ориентированных педагогических технологий являются перенос приоритетов на личность обучаемого и его познавательную деятельность, формирование целостной личности студента, способной собирать, отбирать, анализировать и оценивать информацию. Урок математики является одним из важных звеньев, в этом сложном и длительном процессе по формированию ключевых компетенций будущего специалиста.