Интегрированный урок геометрии и истории по теме "Площади четырехугольников"

Цели урока: формирование представлений о межпредметных связях.

Задачи урока:

Закрепить знания, умения и навыки обучающихся по темам «Площадь фигур», «Теорема Пифагора»;

Совершенствовать навыки решения задач по теме «Площадь»;

Расширить знания обучающихся о истории ремесел в Древней Руси;

Воспитывать интерес к истории родного народа;

Показать связь математики с практической деятельностью людей;

Продолжить развитие памяти, внимания, творческого мышления обучающихся, пространственного мышления.

Техническое обеспечение урока: мультимедийная установка, карточки с заданиями.

Ход урока:

1. Организационный момент.

Прочитайте тему урока.

? Как вы думаете, чем мы сегодня будем заниматься на уроке?

? Какие вопросы возникают у вас, прочитав тему урока?

? Что означает по вашему мнению запись в скобках?

Урок у нас сегодня необычный. На нашем уроке мы совершим путешествие во времени. Это позволят нам сделать задачи, которые связаны с ремеслами Древней Руси. Некоторые задачи предложили вы.

 Прежде чем приступать к решению заданий, я предлагаю вам выполнить небольшую тестовую работу по вариантам с дальнейшей взаимопроверкой. Это поможет вспомнить тот теоретический материал, который нам с вами сегодня понадобиться для успешного выполнения заданий.

2. Актуализация знаний.

Тест с взаимопроверкой по вариантам – смотрите документ

3. Решение задач.

«На площади (Красной) и в соседних улицах каждому товару и каждому промыслу положены особые места и лавки … Торговцы шелком, сукном, золотых дел мастера, сапожники, портные, скорняки, шапошники и другие – все имеют свои особые улицы, где они продают свой товар», - удивлялись иностранцы, посетившие Москву в 17 веке.

? Назовите ремесла, которыми славились русские ремесленники.

Многими ремесленниками славилась Русь! Мы поговорим сегодня о нескольких.

1. Горододельцы – военные инженеры.

Основная задача горододельцев – построение таких сооружений, которые бы затрудняли неприятелю подступы к городам Руси, а главным образом к Москве. Но кроме оборонительной функции эти построения были эстетически уникальными.

 Чтобы сооружение было красивым, оно должно было быть соразмерным. С этой целью мастера Древней Руси применяли следующий способ получения соотношений отрезков : при начертании плана построений прямоугольной формы с шириной а, длину прямоугольника b находили как диагональ квадрата со стороной а.

 На слайде план Тульского кремля. (сообщение ученика о Тульском кремле).

 Задача 1: Вычислите площадь, занимаемую Тульским кремлем, если известно, что ширина его 218 м. (фронтальная работа с классом)

?Выразите ширину через длину. (a=0, 7b)

Это соотношение использовали Древние Русичи при построении городов. Древние Греки при строительстве использовали соотношение размеров, которое называли золотым сечением: a=0, 6b. Получается, что независимо друг от друга древние зодчие Греции и Руси определили почти одинаковые величины соразмерности частей сооружений.

 Еще одно сооружение, о котором хотелось поговорить – Семиглавая башня Белого города. (сообщение ученика о Семиглавой башне)

 Задача 2: Семиглавая башня Белого города в плане являлась шестиугольником со сторонами 14 м. Определите угол между соседними стенами башни. Вычислите площадь фундамента. (120⁰, 294√3 м²)

Решение (составить план решения 3 способами, решение оформить дома )

? Как найти площадь шестиугольника? На какие фигуры можно разбить шестиугольник?

Весь материал – смотрите документ.

Интегрированный урок в 8 классе по теме:

«Мастера России»

(нахождение площади фигур)

Цели урока: формирование представлений о межпредметных связях.

Задачи урока:

• Закрепить знания, умения и навыки обучающихся по темам «Площадь фигур», «Теорема Пифагора»;

• Совершенствовать навыки решения задач по теме «Площадь»;

• Расширить знания обучающихся о истории ремесел в Древней Руси;

• Воспитывать интерес к истории родного народа;

• Показать связь математики с практической деятельностью людей;

• Продолжить развитие памяти, внимания, творческого мышления обучающихся, пространственного мышления.

Техническое обеспечение урока: мультимедийная установка, карточки с заданиями.

Ход урока:

1. Организационный момент.

Прочитайте тему урока.

? Как вы думаете, чем мы сегодня будем заниматься на уроке?

? Какие вопросы возникают у вас, прочитав тему урока?

? Что означает по вашему мнению запись в скобках?

Урок у нас сегодня необычный. На нашем уроке мы совершим путешествие во времени. Это позволят нам сделать задачи, которые связаны с ремеслами Древней Руси. Некоторые задачи предложили вы.

Прежде чем приступать к решению заданий, я предлагаю вам выполнить небольшую тестовую работу по вариантам с дальнейшей взаимопроверкой. Это поможет вспомнить тот теоретический материал, который нам с вами сегодня понадобиться для успешного выполнения заданий.

1. Актуализация знаний.

Тест с взаимопроверкой по вариантам

1 вариант.

1. Выберите верные утверждения:

1. площадь прямоугольника равна произведению его сторон;

2. площадь квадрата равна квадрату его стороны;

3. площадь прямоугольника равна удвоенному произведению двух его соседних сторон.

1. Закончите фразу: «Площадь ромба равна половине произведения …»

1. его сторон;

2. его стороны и высоты, проведенной к этой стороне;

3. его диагоналей.

1. По формуле 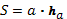 можно вычислить площадь:

1. параллелограмма;

2. треугольника;

3. прямоугольника.

1. Площадь трапеции ABCD с основаниями AB и CD и высотой BH вычисляется по формуле:

1. _;

2. _;

3. _

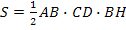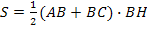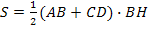1. Выберите верное утверждение.

Площадь прямоугольного треугольника равна:

1. половине произведения стороны на какую-либо высоту;

2. половине произведения его катетов;

3. произведению его стороны на проведенную к ней высоту.

2 вариант.

1. Выберите верные утверждения:

а) площадь квадрата равна произведению его сторон;

б) площадь прямоугольника равна произведению его противолежащих сторон;

в) площадь прямоугольника равна произведению двух его соседних сторон.

2. Закончите фразу: «Площадь параллелограмма равна произведению …»

а) двух его соседних сторон;

б) его стороны на высоту, проведенную к этой стороне;

в) двух его сторон.

3. По формуле 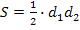_ можно вычислить площадь:

а) параллелограмма;

б) треугольника;

в) ромба.

1. Площадь трапеции ABCD с основаниями BC и AD и высотой СH вычисляется по формуле:

а) _;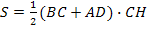

б) _;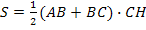

в) _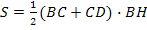

1. Выберите верное утверждение.

Площадь треугольника равна:

а) половине произведения его сторон;

б) половине произведения двух его сторон;

в) половине произведения его стороны на проведенную к ней высоту.

Ответы:

Выпишем формулы, которые нам понадобятся на уроке:

1. S _

2. _

3. _

4. _;

5. _

6. _

7. _

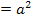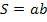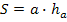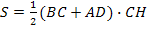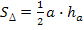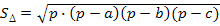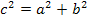1. Решение задач.

«На площади (Красной) и в соседних улицах каждому товару и каждому промыслу положены особые места и лавки … Торговцы шелком, сукном, золотых дел мастера, сапожники, портные, скорняки, шапошники и другие – все имеют свои особые улицы, где они продают свой товар», - удивлялись иностранцы, посетившие Москву в 17 веке.

? Назовите ремесла, которыми славились русские ремесленники.

Многими ремесленниками славилась Русь! Мы поговорим сегодня о нескольких.

1. Горододельцы – военные инженеры.

Основная задача горододельцев – построение таких сооружений, которые бы затрудняли неприятелю подступы к городам Руси, а главным образом к Москве. Но кроме оборонительной функции эти построения были эстетически уникальными.

Чтобы сооружение было красивым, оно должно было быть соразмерным. С этой целью мастера Древней Руси применяли следующий способ получения соотношений отрезков : при начертании плана построений прямоугольной формы с шириной а, длину прямоугольника b находили как диагональ квадрата со стороной а.

На слайде план Тульского кремля.(сообщение ученика о Тульском кремле).

Задача 1: Вычислите площадь, занимаемую Тульским кремлем, если известно, что ширина его 218 м. (фронтальная работа с классом)

218 м

218м

? Как найти длину Тульского кремля?

? Какую теорему будем использовать?

b ² = 218² + 218²

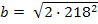_ = 218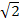_ (м)

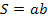
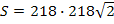_ = 218²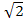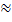_{ } 47524 ∙ 1,4 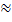_ 47525,4 (м)

? Какую часть от длины составляет ширина?

_ =_ = _ = _{ }

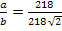?Выразите ширину через длину. (a=0,7b)

Это соотношение использовали Древние Русичи при построении городов. Древние Греки при строительстве использовали соотношение размеров, которое называли золотым сечением: a=0,6b. Получается, что независимо друг от друга древние зодчие Греции и Руси определили почти одинаковые величины соразмерности частей сооружений.

Еще одно сооружение, о котором хотелось поговорить – Семиглавая башня Белого города. (сообщение ученика о Семиглавой башне)

Задача 2: Семиглавая башня Белого города в плане являлась шестиугольником со сторонами 14 м. Определите угол между соседними стенами башни. Вычислите площадь фундамента. (120⁰, 294√3 м²)

Решение (составить план решения 3 способами, решение оформить дома )

? Как найти площадь шестиугольника? На какие фигуры можно разбить шестиугольник?

1 способ: 2 способ: 3 способ:

1 способ:

Найти высоту трапеции.

Основания трапеции 14м и 28м

Найти площадь трапеции.

Площадь шестиугольника равна 2 площадям трапеции.

2 способ:

Треугольники равносторонние.

Найти высоту треугольника.

Найти площадь треугольника.

Площадь трапеции равна 6 площадям треугольника.

3 способ:

Треугольники равносторонние.

Найти площадь треугольника по формуле Герона.

Площадь шестиугольника равна 6 площадям треугольника.

Пожары и войны уничтожили многие города, которые могли бы стоять веками. По всему русскому Северу сохранилось множество удивительных храмов, домов, мельниц, бань выстроенных русскими зодчими. Эти строения помогают представить, какими красивыми были города России в прошлые века.

При строительстве зданий из дерева перед мастерами стояла задача:

Задача 3: Из цилиндрического бревна нужно выпилить брус наибольшего веса. Как это сделать? (задачу решает на доске один ученик самостоятельно, затем объясняет решение классу.)

Задача сводится к тому, чтобы выяснить прямоугольник каких размеров будет иметь наибольшую площадь, если его вписать в квадрат.

Обозначим одну из сторон прямоугольника через х.

Диагональ прямоугольника равна 2R.

По теореме Пифагора выразим другую сторону прямоугольника:

Найдем площадь прямоугольника:

Возведем в квадрат обе части равенства:

Найдем сумму множителей

Т.е. при любых значениях х сумма не изменится и буде равна _.

Значит наибольшим их произведение будет, если

сторона вписанного квадрата.

Получили, что брус будет иметь наибольший объем, а значит и вес, если сечение бруса есть квадрат, вписанный в окружность.

1. Кузнецы

Производство железа – одно из древнейших на Руси. Из железной руды, которой было много по болотам лесостепной части страны, выплавляли крицы – губчатое железо, которое затем под молотом кузнецов уплотнялось. Затем из него выковывали различные изделия. Каждый кузнец занимался ковкой только одного вида изделия. Так кузнецы, изготавливавшие щиты, назывались – щитниками, изготавливавшие кольчуги – бронниками, гвозди – гвоздочниками, иголки для шитья – игольниками … Российские кузнецы славились своим мастерством. Их работу высоко ценили за границей. Недаром крымский хан Менгли-Гирей, союзник Ивана III в борьбе с ханом Ахмедом в 1480 г., не раз просил прислать ему и его вельможам доспехи русской работы.

Задача 4: Определите массу щита, выкованного из стали, если он имеет форму ромба периметром 20 дм, с большей диагональю 8 дм. (Толщина щита 1см). Формула для вычисления массы предмета в сталелитейной промышленности , если k = 8 на 1см² площади изделия при ширине 1см.

1. Гончары

Невозможно себе представить быт человека, жившего в средние века, без предметов, изготовленных гончарами.

Они делала горшки, миски и кувшины. Изготовляли даже погремушки, окрашенные красными полосами и наполненные глиняными шариками.

Изделия из глины были дешевыми, поэтому получили широкое распространение.

В 14 веке в Москве начали изготавливать красную черепицу и покрывать крыши домов. В 1701 – 1702 гг мастера Андрей и Иван Рудаковы изготовили зеленую черепицу для покрытия глав церквей.

Задача 5: Какое количество рядов черепицы размером 41 x 24 см необходимо уложить на части крыши, имеющей форму равнобедренной трапеции. Если известно, что одно из оснований в 3 раза меньше другого, высота составляет 75% от большего основания, а площадь этой части крыши 72 м².

1. Итоги урока.

Мы поговорили с вами не о всех ремеслах, которыми славилась Древняя Русь. Много ремесленников самых разных профессий жили и работали в Москве и других городах России. И чем бы они не занимались – писали иконы или делали ювелирные изделия, отливали свечи или ткали холст, всегда ценилось мастерство – умение делать вещи нужные, добротные и красивые, добрым людям на загляденье.

Выставление оценок за урок.

1. Домашнее задание

Выполнить на отдельных листах.

1. Найти или придумать задачи на нахождение площадей фигур, связанные с ремеслами Руси.

2. Оформить решения для задачи №2 (о Семиглавой башне Белого города) по рядам.

1. Рефлексия.

1. Я сегодня на уроке узнал…

2. Я сегодня на уроке научился…

3. Меня удивило …

4. На уроке мне понравилось …

5. Мне нужно еще поработать над …