ЕГЭ Задание №5 с использованием модуля SCHOOL на языке Pascal.Net

Задание 5

Посимвольное двоичное преобразование

102 N 2 N 10 R 2 =N 2 +’01’ R 10 102 " width="640"

чёт

нечёт

Задание 5 

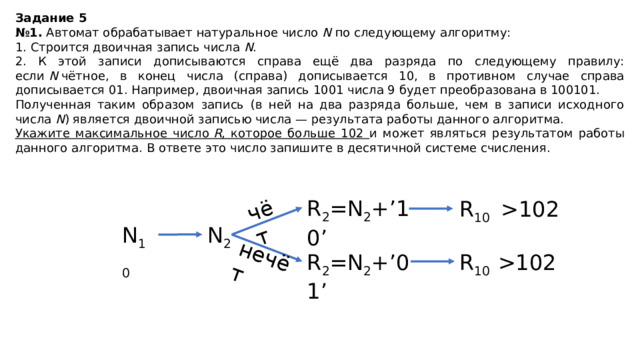
№ 1. Автомат обрабатывает натуральное число  N  по следующему алгоритму:

1. Строится двоичная запись числа  N .

2. К этой записи дописываются справа ещё два разряда по следующему правилу: если  N  чётное, в конец числа (справа) дописывается 10, в противном случае справа дописывается 01. Например, двоичная запись 1001 числа 9 будет преобразована в 100101.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа  N ) является двоичной записью числа — результата работы данного алгоритма.

Укажите максимальное число  R , которое больше 102 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

R 2 =N 2 +’10’

R 10 102

N 2

N 10

R 2 =N 2 +’01’

R 10 102

Что нужно знать :

• сумма двух цифр в десятичной системе счисления находится в диапазоне от 0 до 18 (9+9)
• в некоторых задачах нужно иметь представление о системах счисления (могут использоваться цифры восьмеричной и шестнадцатеричной систем счисления)
• бит чётности – это дополнительный контрольный бит, который добавляется к двоичному коду так, чтобы количество единиц в полученном двоичном коде стало чётным; если в исходном коде уже было чётное количество единиц, дописывается 0, если нечётное – дописывается 1.
• при добавлении к двоичной записи числа нуля справа число увеличивается в 2 раза
• чтобы отбросить последнюю цифру в двоичной записи, нужно разделить число на 2 нацело (остаток отбрасывается)

Модуль School (англ. «школа»)

Модуль School (англ. «школа») содержит реализацию алгоритмов, часто встречающихся в школьных задачах

Перевод из десятичной системы счисления

###

uses School;

var n:=ReadInteger;

var r2:=Bin(n);

var r8:=Oct(n);

var r16:=Hex(n);

Pr(r2,r8,r16)

###

uses School;

var n:=ReadInteger;

var r2:=Bin(n).Pr;

var r8:=Oct(n).Pr;

var r16:=Hex(n).Pr;

//Pr(r2,r8,r16)

###

uses School;

var n:=ReadInteger;

var r2:=bin(n).Pr;

var r8:=Oct(n).Pr;

var r16:=hex(n).Pr;

Pr(Dec(r2,2))

• А09 16 – 2380 10 {ответ дать в 8 сс}
• А09 16 – 2380 10 {ответ дать в 8 сс}

###

uses school;

var r:=dec( 'A09' , 16 )- 2380 ;

pr(oct(r))

b) А09 16 – 2380 10 {ответ дать в 13 сс}

###

uses school;

var r:=dec( 'A09' , 16 )- 2380 ;

pr(tobase(r, 13 ))

c) 1100110100 2 - 1001 8 {ответ дать в 16 сс}

###

uses school;

var d2:=dec( '1100110100' , 2 )-dec( '1001' , 8 );

pr(hex(d2))

###

uses school;

var r:=dec( '1100110100' , 2 )-dec( '1001' , 8 );

pr(tobase(r, 16 ))

###

uses school;

var r:=(dec( '3A5' , 16 )+dec( '73' , 9 ))*dec( '23' , 7 )-dec( '211' , 9 );

pr(tobase(r, 13 ))

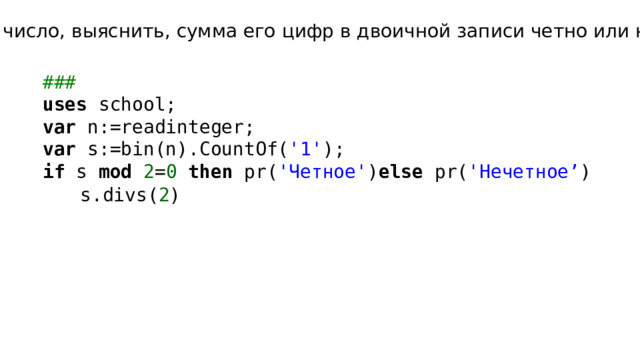
Дано число, выяснить, сумма его цифр в двоичной записи четно или нет

###

uses school;

var n:=readinteger;

var s:=bin(n).CountOf( '1' );

if s mod 2 = 0 then pr( 'Четное' ) else pr( 'Нечетное’ )

s.divs( 2 )

Срезы

Stroka[start:stop:step]

###

var s:=readstring;

//var k:=length(s);

pr(s[^ 2 :])

###

uses school;

var (n1,n2):=readinteger2;

var r1:=bin(n1);

var r2:=bin(n2);

var r:=r1[: 3 ]+r2[^ 2 :];

pr(r)

151 then mn:=min(mn,dec(r, 2 )); end ; pr(mn); " width="640"

###

uses school;

var r:= '' ;

var mn:=maxint;

for var n:= 4 to 151 do

begin

var nb:=bin(n);

if n.Divs( 3 ) then r:=nb+nb[^ 3 :] else

r:=nb+bin((n mod 3 )* 3 );

if dec(r, 2 ) 151 then mn:=min(mn,dec(r, 2 ));

end ;

pr(mn);

102 N 2 N 10 R 2 =N 2 +’01’ R 10 102 " width="640"

чёт

нечёт

Задание 5 

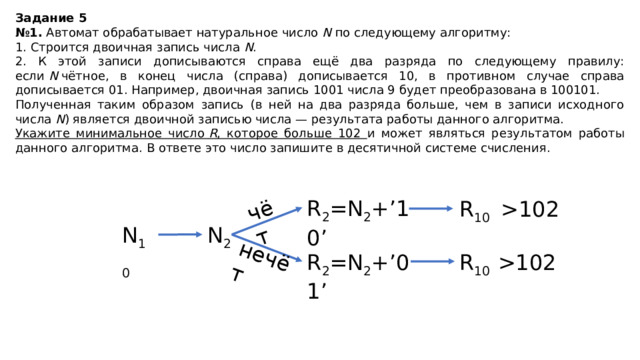
№ 1. Автомат обрабатывает натуральное число  N  по следующему алгоритму:

1. Строится двоичная запись числа  N .

2. К этой записи дописываются справа ещё два разряда по следующему правилу: если  N  чётное, в конец числа (справа) дописывается 10, в противном случае справа дописывается 01. Например, двоичная запись 1001 числа 9 будет преобразована в 100101.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа  N ) является двоичной записью числа — результата работы данного алгоритма.

Укажите минимальное число  R , которое больше 102 и может являться результатом работы данного алгоритма. В ответе это число запишите в десятичной системе счисления.

R 2 =N 2 +’10’

R 10 102

N 2

N 10

R 2 =N 2 +’01’

R 10 102

102 N 10 N 2 R 2 =N 2 +’01’ R 10 102 Переведем число 103 в двоичную систему. R 2 = 11001 11 11001 N 2 +1 + N 2 1 11010 2. Число четное, добавляем 10. Переведем двоичное число 1101010 в десятичную систему счисления. " width="640"

чёт

нечёт

1 способ : Калькулятор (вид – программист)

R 2 =N 2 +’10’

R 10 102

N 10

N 2

R 2 =N 2 +’01’

R 10 102

• Переведем число 103 в двоичную систему.

R 2 = 11001 11

11001

N 2 +1

+

N 2

1

11010

2. Число четное, добавляем 10. Переведем двоичное число 1101010 в десятичную систему счисления.

102 then pr(dec(r, 2 )); end Rn на 2 разряда, поэтому n" width="640"

###

uses school;

for var n:= 2 to 26 do

begin

var r:=bin(n);

if n mod 2 = 0 then r:=r+ '10'

else r:=r+ '01' ;

if dec(r, 2 ) 102 then pr(dec(r, 2 ));

end

Rn на 2 разряда, поэтому n

Демо 2023

40 then Pr(n) end ; " width="640"

###

uses School;

for var n:= 4 to 40 do

begin

var r:=bin(n);

if r.countof( '1' ) mod 2 = 0 then

r:= '10' +r[ 3 :]+ '0'

else

r:= '11' +r[ 3 :]+ '1' ;

if Dec(r, 2 ) 40 then Pr(n)

end ;

102 then Println(dec(r, 2 ),N); end ; end . " width="640"

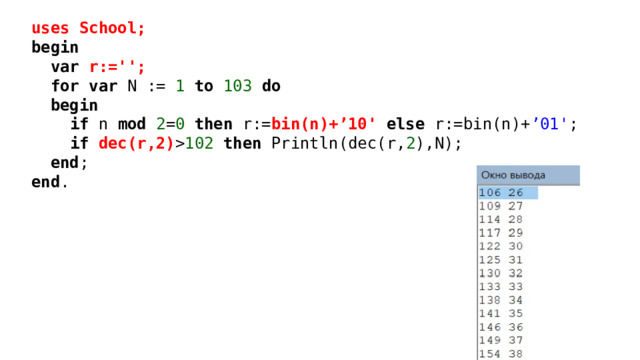
uses School;

begin

var r:='';

for var N := 1 to 103 do

begin

if n mod 2 = 0 then r:= bin(n)+’10' else r:=bin(n)+ ’01' ;

if dec(r,2) 102 then Println(dec(r, 2 ),N);

end ;

end .

(демо-2022) . На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

• Строится двоичная запись числа N.
• К этой записи дописываются справа ещё два разряда по следующему правилу:

а) складываются все цифры двоичной записи числа N, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия – справа дописывается остаток от деления суммы её цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите такое наименьшее число N, для которого результат работы данного алгоритма больше числа 77. В ответе это число запишите в десятичной системе счисления.

77 then pr(n) end " width="640"

###

uses school;

for var n:= 1 to 77 do

begin

var r:=bin(n);

if r.CountOf( '1' ) mod 2 = 0 then r:=r+ '00'

else r:=r+ '10' ;

if dec(r, 2 ) 77 then pr(n)

end

№  8094       

На вход алгоритма подаётся натуральное число  N . Алгоритм строит по нему новое число  R  следующим образом.

1) Строится двоичная запись числа  N .

2) К этой записи дописываются справа ещё два разряда по следующему правилу:

а) складываются все цифры двоичной записи, и остаток от деления суммы на 2 дописывается в конец числа (справа). Например, запись 11100 преобразуется в запись 111001;

б) над этой записью производятся те же действия — справа дописывается остаток от деления суммы цифр на 2.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа  N ) является двоичной записью искомого числа  R .

Укажите минимальное число  R , которое превышает 43 и может являться результатом работы алгоритма. В ответе это число запишите в десятичной системе.

Ответ: 46.

144. ( Досрочный ЕГЭ-2018 ) На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число следующим образом.

1) Строится двоичная запись числа N.

2) К этой записи дописываются справа ещё два разряда по следующему правилу: если N чётное, в конец числа (справа) дописываются два нуля, в противном случае справа дописываются две единицы. Например, двоичная запись 1001 числа 9 будет преобразована в 100111.

Полученная таким образом запись (в ней на два разряда больше, чем в записи исходного числа N) является двоичной записью числа – результата работы данного алгоритма. Укажите минимальное число N, для которого результат работы алгоритма будет больше 115. В ответе это число запишите в десятичной системе счисления.

29

140. На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1) Строится двоичная запись числа N.

2) К этой записи дописывается (дублируется) последняя цифра.

3) Затем справа дописывается бит чётности: 0, если в двоичном коде полученного числа чётное число единиц, и 1, если нечётное.

4) К полученному результату дописывается ещё один бит чётности.

Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, большее 66, которое может быть получено в результате работы этого алгоритма. В ответе это число запишите в десятичной системе.

78

147. На вход алгоритма подаётся натуральное число N. Алгоритм строит по нему новое число R следующим образом.

1) Строится двоичная запись числа N.

2) К этой записи дописывается (дублируется) последняя цифра.

3) Затем справа дописывается 0, если в двоичном коде числа N чётное число единиц, и 1, если нечётное ( Имеется в виду исходное число ) .

4) К полученному результату дописывается ещё один бит чётности так, чтобы количество единиц в двоичной записи полученного числа стало чётным.

Полученная таким образом запись (в ней на три разряда больше, чем в записи исходного числа N) является двоичной записью искомого числа R. Укажите минимальное число R, большее 105, которое могло получиться в результате работы автомата. В ответе это число запишите в десятичной системе.

Ответ 111