ЕГЭ Планиметрия вычисление длин и площадей. Задание №3 Тренажёр

Задание №3 ЕГЭ ПЛАНИМЕТРИЯ: вычисление длин и площадей

Тренажёр

Учитель математики

Лебах Марина Геннадьевна

МБОУ «СОШ №1 г. Строитель»

Чтобы найти площадь фигуры

• площади треугольника;
• площади четырехугольников: прямоугольника, квадрата, ромба, параллелограмма, трапеции;
• площади круга ;
• площади сектора.

• решать простые планиметрические задачи;
• производить вычисления по известным формулам.

Надо знать формулы:

Надо уметь:

Площадь можно вычислить:

• либо по клеточкам,
• либо по координатам,
• либо по формулам.

Количество баллов за правильное решение: 1.

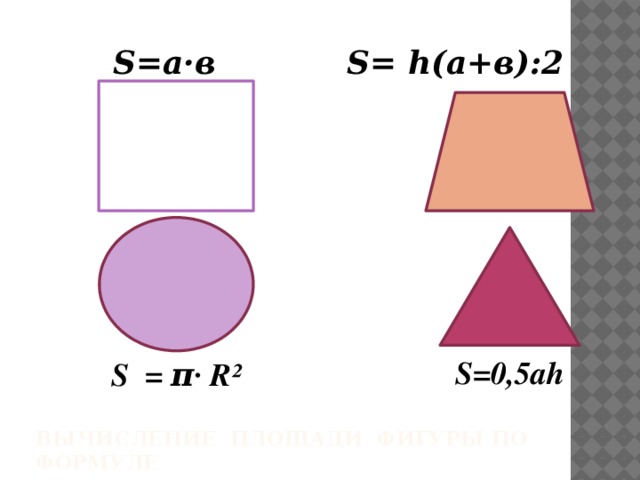
S= h(а+в):2

S=а·в

S=0,5ah

S = π∙ R²

Вычисление площади фигуры по формуле

Задача 1

Найдите площадь заштрихованной фигуры, считая стороны квадратных

клеток равными 1.

4

Ответ: 28

7

Задача 2

Найдите площадь Δ ABC , считая стороны квадратных клеток равными 1.

3

6

Ответ: 9

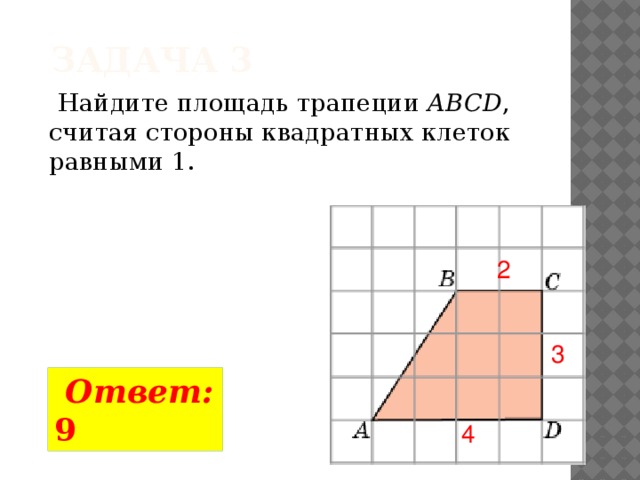
Задача 3

Найдите площадь трапеции ABCD , считая стороны квадратных клеток равными 1.

2

3

Ответ: 9

4

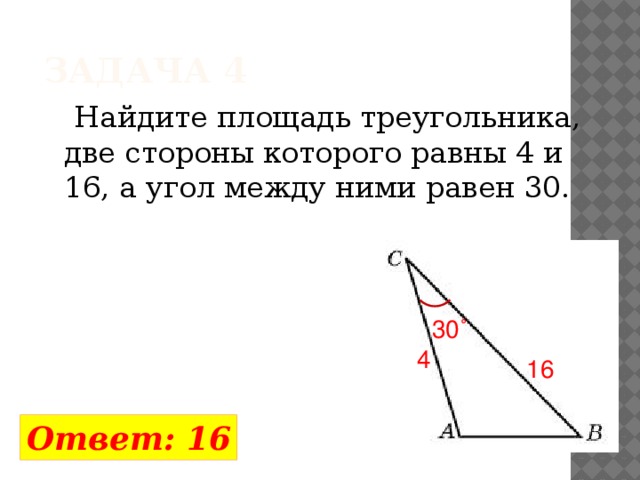
Задача 4

Найдите площадь треугольника, две стороны которого равны 4 и 16, а угол между ними равен 30.

30˚

4

16

Ответ: 16

Задача 5

Боковая сторона равнобедренного треугольника равна 5, а основание равно 8. Найдите площадь этого треугольника.

5

3

5

4

4

Ответ: 12

8

Задача 6

Найдите площадь ромба, если его диагонали равны 6 и 10.

6

10

Ответ: 30

Задача 7

Найдите площадь S сектора, считая стороны квадратных клеток равными 1.

В ответе укажите

S/π .

√ 5

R

1

2

90˚

Ответ: 1,25

R=1

Задача 8

Найдите площадь сектора круга радиуса 1, длина дуги которого

равна 2.

2

Ответ: 1

2

Задача 9

Найдите площадь заштрихованной фигуры, считая стороны квадратных клеток равными 1.

Ответ: 14

Задача 10

Найдите площадь заштрихованной фигуры, считая стороны квадратных клеток равными 1.

Ответ: 15

Задача 11

Периметр треугольника равен 10, а радиус вписанной окружности равен 2. Найдите площадь этого треугольника.

Ответ: 10

Задача 12

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 120. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника. В ответе запишите S/√3.

Ответ: 100

Задача 13

Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите

площадь большего

многоугольника.

Ответ: 50

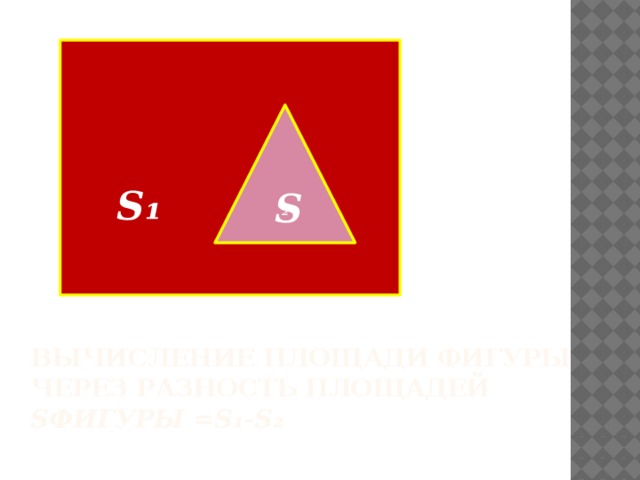
₂

S₁

S

Вычисление площади фигуры через разность площадей Sфигуры =S₁-S₂

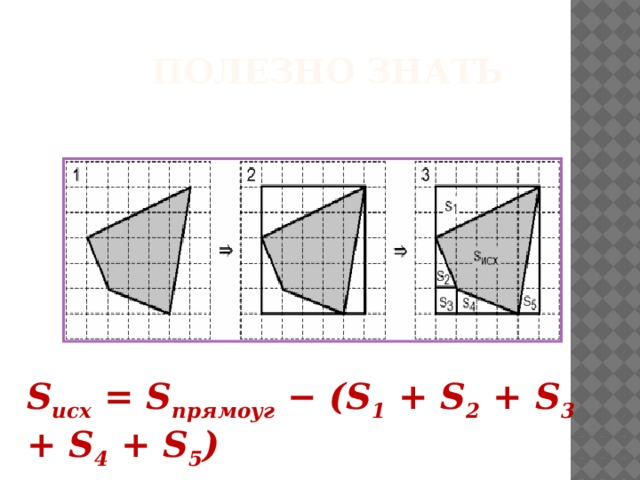
Полезно знать

S исх = S прямоуг − (S 1 + S 2 + S 3 + S 4 + S 5 )

Задача 14

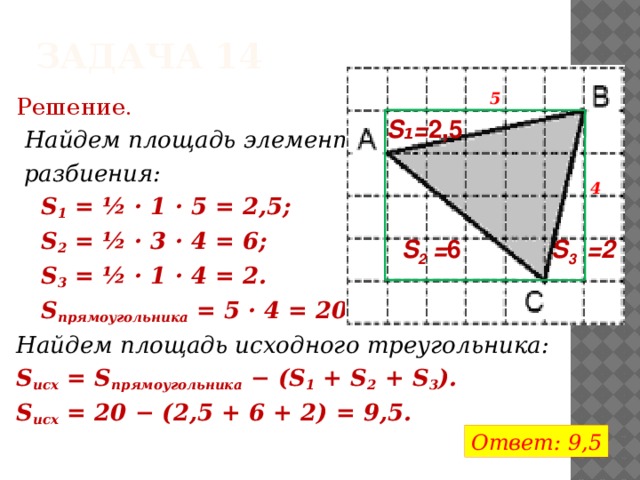
Найти площадь треугольника ABC, изображенного на рисунке, считая стороны квадратных клеток равными 1.

Задача 14

Решение.

Найдем площадь элементов

  разбиения:

S 1 = ½ · 1 · 5 = 2,5;

S 2 = ½ · 3 · 4 = 6;

S 3 = ½ · 1 · 4 = 2.

S прямоугольника = 5 · 4 = 20.

Найдем площадь исходного треугольника:

S исх = S прямоугольника − (S 1 + S 2 + S 3 ).

S исх = 20 − (2,5 + 6 + 2) = 9,5.

5

S₁= 2,5

4

S 2 = 6

S 3 =2

Ответ: 9,5

Задача 15

Найдите площадь Δ ABC , считая стороны квадратных клеток равными 1.

12,5

2

1

2

Ответ: 7,5

Задача 16

Найдите площадь ромба ABCD , считая стороны квадратных клеток равными 1.

1

1,5

1,5

1,5

1

1,5

Ответ: 8

Задача 17

2:√π

4:√π

Найдите площадь кольца, ограниченного концентрическими окружностями,

радиусы которых

равны 2:√π и 4:√π .

Ответ: 12

Задача 18

Найдите площадь S кольца, считая стороны квадратных клеток равными 1.

В ответе укажите S/π.

R

2

√ 8

r= 2

2

Ответ: 4

Задача 19

Найдите площадь трапеции ABCD , считая стороны квадратных клеток равными 1.

Ответ:9.

Задача 20

Найдите площадь четырехугольника ABCD , считая стороны квадратных клеток равными 1.

Ответ:6

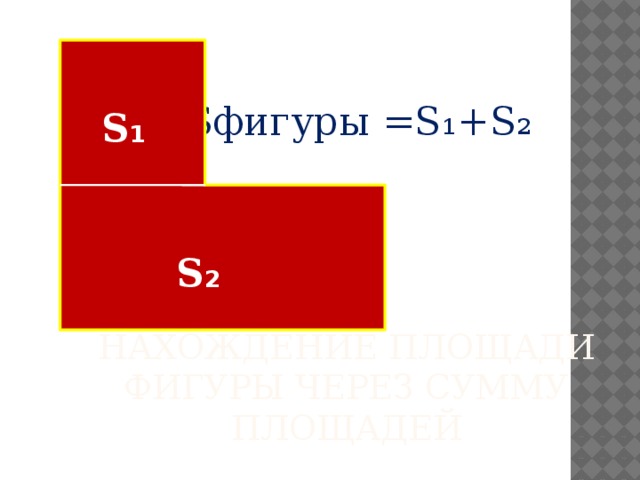
Sфигуры =S₁+S₂

S ₁

S ₂

Нахождение площади фигуры через сумму площадей

Задача 21

Найдите площадь прямоугольника ABCD , считая

стороны квадратных

клеток равными 1.

5

5

Ответ: 10

Задача 22

Найдите площадь четырехугольника ABCD , считая

стороны квадратных

клеток равными 1.

2

4

Ответ:8.

Задача 23

Найдите площадь

пятиугольника, считая

стороны квадратных

клеток равными 1.

2

3

Ответ:16.

4

Задача 24

Найдите площадь

фигуры, считая

стороны квадратных

клеток равными 1.

1

1

3

4

1

Ответ:15

Задача 25

Найдите площадь

фигуры, считая

стороны квадратных

клеток равными 1.

2

2

1

1

3

2

Ответ:13.

4

у

n

с

к

m

х

d

а

в

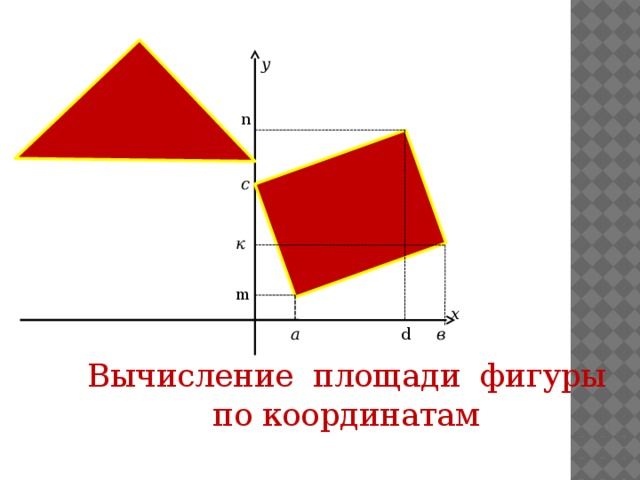
Вычисление площади фигуры по координатам

Задача 26

Найдите площадь треугольника, вершины которого имеют координаты

(1; 1), (4; 4), (5;1).

3

4

Ответ: 6

Задача 27

Найдите площадь четырехугольника, вершины которого имеют

координаты (1; 0),

(0; 2), (4; 4), (5; 2) .

2

5

Ответ: 10

Задача 28

Найдите площадь закрашенной фигуры на координатной плоскости.

Ответ: 24

Вычисление элементов фигуры

• Сторон

• Диагоналей

• Высот

• Углов

Задача 29

Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами

4 и 16.

16

4

S=64

Ответ: 8

Метод координат

у=kx+b

А

(х₁; у₁)

С

(х; у)

α

В

(х₂; у₂)

О

Длина отрезка:

АВ=√(х₁-х₂)²+(у₁-у₂)²

Координаты середины отрезка:

х= (х₁+х₂):2 у= (у₁+у₂):2

Угловой коэффициент k=tg α прямой у=kx+b .

Задача 30

Найдите диагональ квадрата, если его площадь равна 8.

4

√ 8

Ответ: 4

√ 8

Задача 31

Площадь прямоугольного треугольника равна 21. Один из его катетов равен 6. Найдите другой катет.

S=21

Ответ:7.

6

Задача 32

Основания равнобедренной трапеции равны 14 и 26, а ее площадь равна 160. Найдите периметр трапеции.

14

S=160

10

8

10

8

Ответ:60

6

6

26

Задача 33

Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?

Ответ: 2

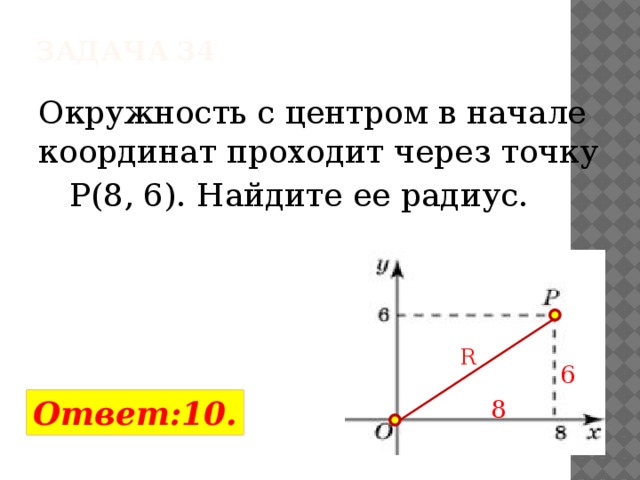
Задача 34

Окружность с центром в начале координат проходит через точку

P(8, 6). Найдите ее радиус.

R

6

Ответ:10.

8

Задача 35

Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6).

R

M

Ответ:5.

Задача 36

Найдите :

• 1)угловой коэффициент прямой, проходящей через точки с координатами(2, 0) и (0, 2);

• 2) угол между

прямой и осью ОХ.

Ответ:-1.

2

α

Ответ:135.

2

Задача 37

Точки O(0, 0), A(6, 8), B(6, 2) и C являются вершинами параллелограмма. Найдите ординату точки C.

Ответ:6.

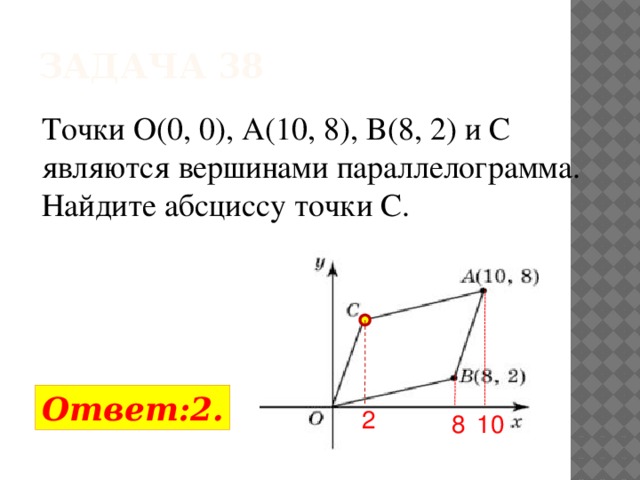
Задача 38

Точки O(0, 0), A(10, 8), B(8, 2) и C являются вершинами параллелограмма. Найдите абсциссу точки C.

Ответ:2.

2

10

8

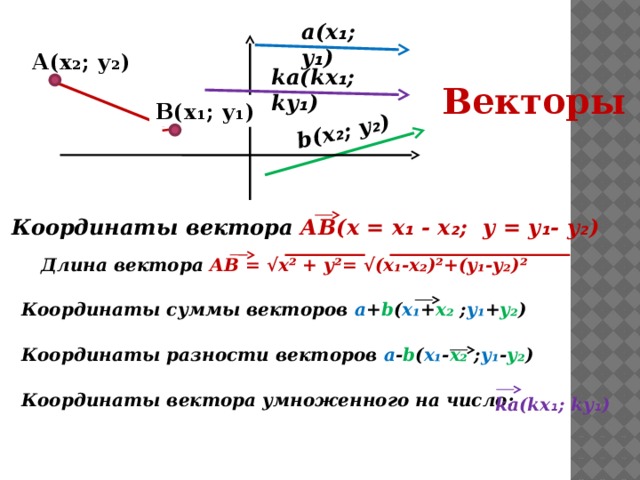
b(х ₂ ; у ₂ )

а(х ₁ ; у ₁ )

А(х₂; у₂)

kа(kх ₁ ; kу ₁ )

Векторы

В(х₁; у₁)

Координаты вектора АВ(х = х ₁ - х ₂ ; у = у ₁ - у ₂ )

Длина вектора АВ = √х² + у²= √(х₁-х₂)²+(у₁-у₂)²

Координаты суммы векторов а + b ( х₁ + х₂ ; у₁ + у₂ )

Координаты разности векторов а - b ( х₁ - х₂ ; у₁ - у₂ )

Координаты вектора умноженного на число:

kа(kх ₁ ; kу ₁ )

Задача 39

Найдите : 1) ординату вектора а; 2)квадрат длины вектора а; 3) квадрат длины вектора а-b ; 4) длину вектора

а+b.

Ответ:6

Ответ:40

Ответ:40

Ответ: 10√2

Задача 40

Вектор с началом в точке A(2,4) имеет координаты (6, 2). Найдите абсциссу точки B.

Ответ:8

8

Задача 41

Две стороны прямоугольника ABCD равны 8 и 6 . Найдите длину суммы векторов АВ и АД.

6

Ответ:10

8

Задача 42

Диагонали ромба ABCD равны 8 и 12. Найдите длину разности векторов:

1)АВ-АД;

2)АД-АВ;

3)АД+АВ. .

Ответ:8

Ответ:8

8

12

Ответ:12

Удачи и успехов !