Гармонические коледания

Урок 10 класс.

Гармонические колебания.

Цели урока:

1. Образовательная

   • Сформировать представление о гармонических колебаниях, их использования, о гармоническом анализе

   • Сформировать умения по построению гармонических колебаний как с помощью преобразований, так и помощью сложения;

2. развивающая

развитие познавательного интереса, основ ориентировочных действий;

1. воспитательная

2. способствовать формированию таких качеств личности учащихся как уважение друг к другу, взаимоподдержки

1. Введение.

Изучая многие школьные предметы, в частности, физику, вы часто встречались с различными видами зависимостей, которые описывают реальные процессы. Эти процессы обычно связаны с большим количеством переменных и зависимостей между ними. В то же время можно отвлечься от каких-то частных деталей, сосредоточив свое внимание лишь на некоторых сторонах процесса, идеализировав условия, в которых оно протекает. Тогда удается построить математическую модель процесса, состоящую в перечислении основных характеристик и тех связей, которые между ними имеются. Так, например, в кинематике равномерного движения изучаются процессы, описываемые линейной функцией, в кинематике криволинейного движения – квадратичная функция, «мощность, энергия» - степенные функции, «идеальные газы» - обратная пропорциональность. Встречались ли процессы, графики которых – синусоиды?

Сегодня мы познакомимся с такими и более сложными процессами и посмотрим, как математический аппарат, в частности, действия с графиками и их преобразования описывают и характеризуют эти процессы.

1. Основная часть.

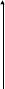
Давайте вспомним, как мы получили график функции y = sin x.

Рассмотрим следующий реальный процесс: шарик, движущейся по данной окружности в положительном направлении, тогда проекция этого шарика на ось ОУ будет колебаться по отрезкам длиной ВС и описываться данной синусоидой. Если наблюдение за этим шариком мы начнем не с начальной точки, т.е. при t = 0 уже будет некоторое значение ординаты, то что будет с графиком? А если увеличить или уменьшить скорость? А если взять нить большей длины? Что будет с графиком? А какой вид примет формула?

y = A sin (ωt + φ).

(про косинус).

Тема урока. Гармонические колебания.

Гармонические колебания – это процесс, который может быть описан функцией вида

y = A sin (ωt + φ), где

А – амплитуда колебаний,

φ – начальная фаза.

ω – циклическая частота (она показывает сколько полных колебаний совершает точка за 2π единиц времени) Т = 2π/ ω

Можно ли график гармонического колебания записать с помощью косинуса?

Примеры.

1) Движение проекции вращающегося шарика на ось.

1. Колебания конца упругой пружины. (как вам кажется, почему называются гармонические колебания)

3) Чистый звуковой тон. (в физике вы об этом будете говорить подробнее)

Музыка, которую мы слышим, представляет собой наложение чистых тонов, поэтому часто колебания приходится складывать.

Попробуем сделать это математически.

П ример. Дано: y₁ = sin 2x; y₂ = cos 2x.. 1)Построить в одной системе координат график функции

y = sin 2x + cos 2x

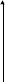
2) Чем является график получившейся функции? Попробуем записать ее уравнение

1. Какие варианты получились – назвать (Наверно, это было сделать не очень удобно)

   • Но раз график – синусоида, давайте попробуем получить формулу с помощью тригонометрических преобразований.

II способ __ _ _ _ _

sin 2x + cos 2x = √2 (1/√2 sin 2x + 1/√2 cos 2x) = √2 (cos π/4 sin 2x + sin π/4 cos 2x) = √2 sin (2x + π/4).

_

Т.о. имеем у = = √2 sin (2x + π/4). Назовите последовательность его построения

1. y = sin x

2. y = sin 2x

3. y = sin 2 (x + π/8)

4. y = √2 sin (2x + π/4). Показать на чертеже.

С равните с получившейся вашей формулой. (указать А, ω, φ.).

Учащиеся выполняют №1 из листа контроля знаний

Всегда ли при сложении простых гармонических колебаний получится гармоническое колебание

Самостоятельная работа. (выполняют №2)

Пример. y = sin 3x; y = cos 2x. У вас есть уже построенные графики в одной системе координат и проведены прямые по которым нужно выполнить сложение.

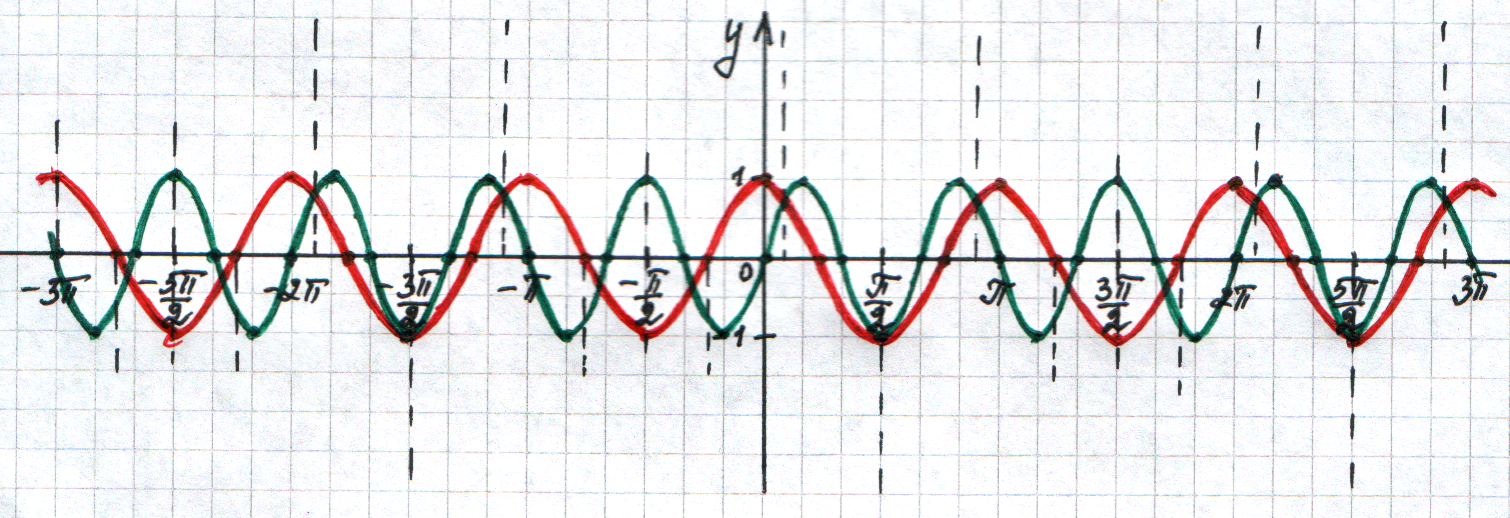
Гармоническое ли колебание получилось? Но периодическая ли функция?

Как вы думаете, почему здесь не получилось гармоническое колебание? (делается вывод о сложении гармонических колебаний с одинаковыми и разными частотами)

Но практически, при исследованиях в области, например, акустики приходится складывать множество колебаний, разных частот, амплитуд и первоначальных смещений, т.е. проводить некоторый анализ, этот анализ делается и, скажем, при изучении приливов и отливов для их предсказания. Анализ это называется гармоническим. Проведем его и мы. Для этого мы будем складывать разные синусоиды(гармоники) с разными частотами и амплитудами без начальных фаз, т.е. имеет следующий ряд

Практическая работа. (выполняют №3 – компьютерное сложение гармоник, используется программа, созданная в школе)

• Садитесь за компьютеры.

1. у =sin 2x + cos 2x

2. у = sin 3х + cos 2x

3) Далее у вас написано, что нужно сделать, выполняйте работу.

И в 1822 году математикой была совершена революция в физике. Ее совершил фран. математик и физик Жан Батист Жозеф Фурье (1768-1830) Теорема Фурье (впервые доказана Фурье, в наше время остается предметом исследований и находит многочисленные применения в науке):

Л юбое (повторяющееся) движение можно рассматривать как результат наложения простых гармонических движений. Любую волну независимо от ее формы можно рассматривать как сумму простых гармонических волн.

III. Заключение

Контрольные листы сдали. Давайте теперь вместе посмотрим на те графики, которые у вас получились.

Построение 1. Результат сложения у = х²

Построение 2. Результат сложения у = |х|

Построение 3. Результат сложения у = х

(Анализ результатов)

В теореме Фурье сказано, что (повторяющееся) движение можно разложить на гармоники, т.е. здесь вы получили на отрезке, на том на котором складывались эти гармоники. Поэтому какой бы периодическое движение не было, его можно разложить на гармонические составляющие (есть, правда некоторые ограничения, например, для функции у = tgx, те кто заинтересовался, можете сами посмотреть к следующему уроку, а подробно вы будете изучать в вузе, хотя в 11 классе мы сделать проектную работу, а пока

III.Выводы:

1. Этот вид движения весьма распространен

2. Поддается простому математическому описанию

3. Согласно теореме Фурье, любое периодическое движение, согласно теореме Фурье можно разложить на простые гармонические составляющие.

IV. Домашнее задание.