Получите свидетельство
Вход
Электронный справочник, 7 класс
Геометрические фигуры.
Свойства геометрических фигур.
Автор: Ющиева М.В.
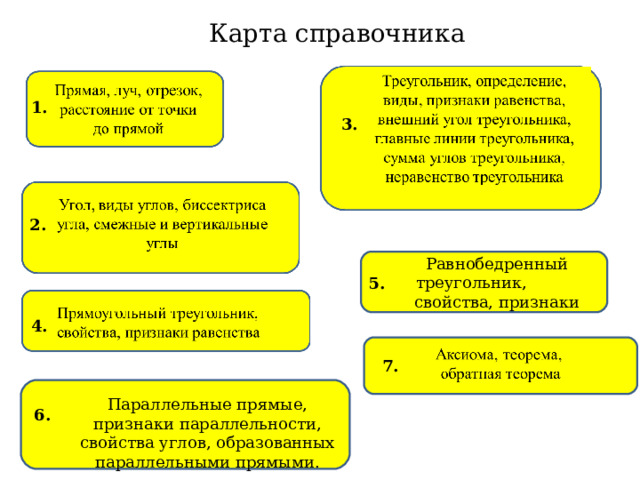
Карта справочника
1.
3.
2.
Равнобедренный треугольник,
свойства, признаки
5.
4.
7.
Параллельные прямые, признаки параллельности, свойства углов, образованных параллельными прямыми.
6.
Тема 1
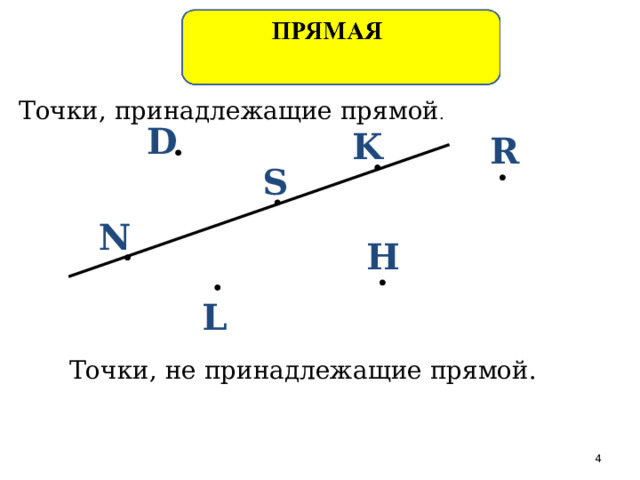
Точки, принадлежащие прямой .
D
K
R
S
N
H
L
Точки, не принадлежащие прямой.
, а
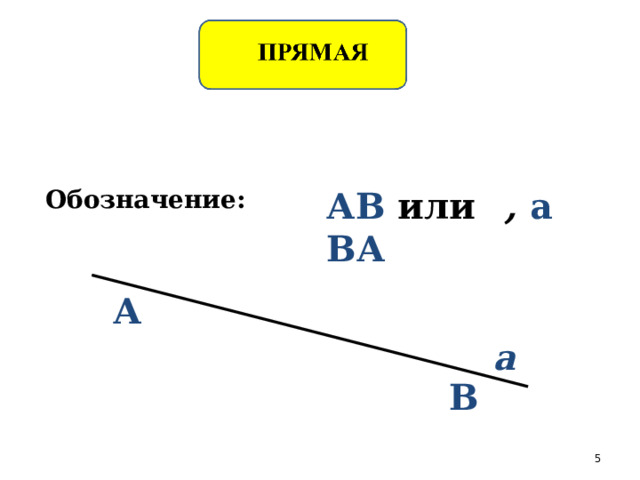
Обозначение:
АВ или ВА
А
а
В
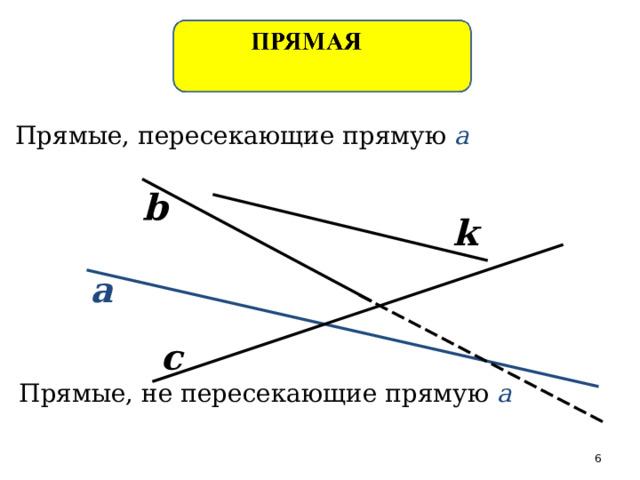
Прямые, пересекающие прямую а
b
k
а
c
Прямые, не пересекающие прямую а
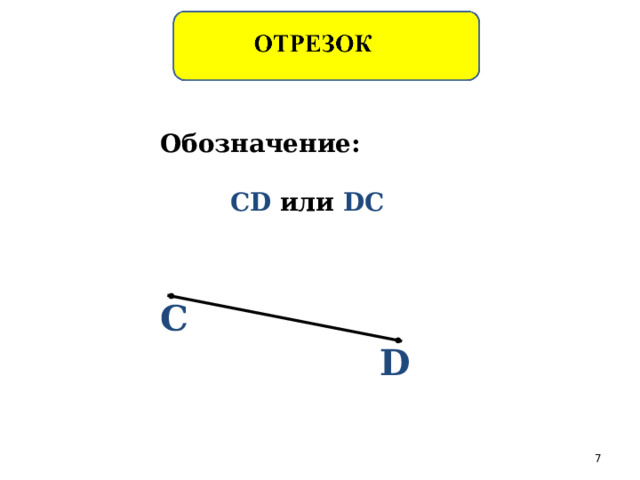
Обозначение:
CD или DC
C
D
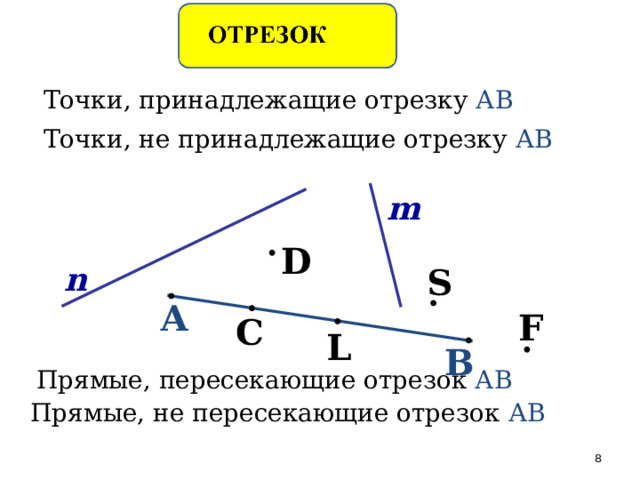
Точки, принадлежащие отрезку АВ
Точки, не принадлежащие отрезку АВ
m
D
n
S
А
F
C
L
В
Прямые, пересекающие отрезок АВ
Прямые, не пересекающие отрезок АВ
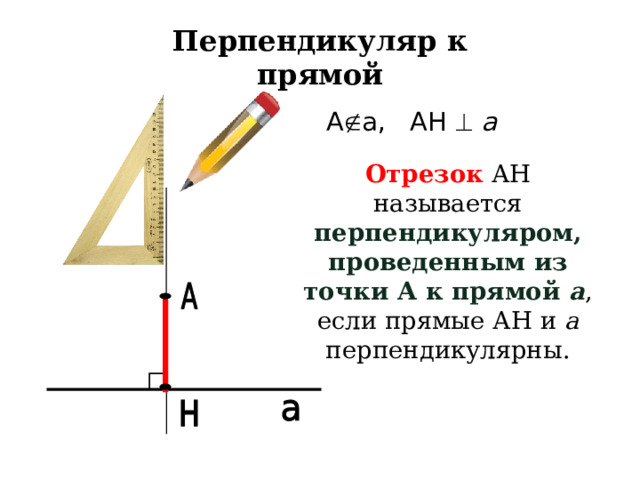
Перпендикуляр к прямой
А а, АН а
Отрезок АН называется перпендикуляром, проведенным из точки А к прямой а , если прямые АН и а перпендикулярны.
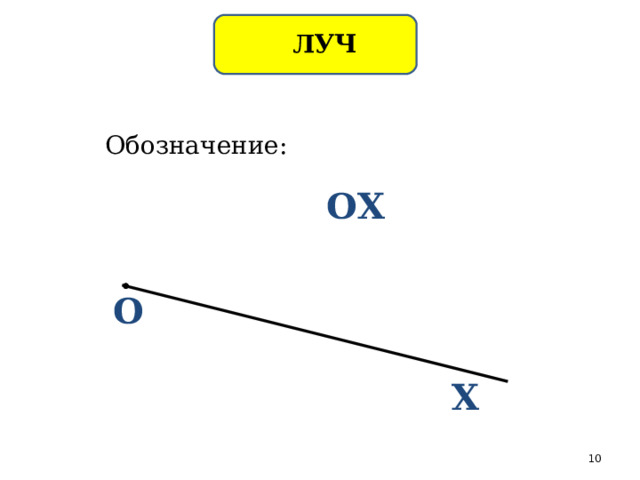
ЛУЧ
Обозначение:
ОХ
О
Х
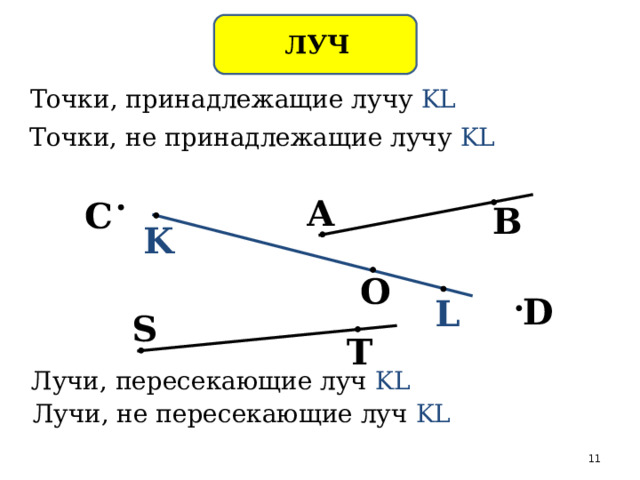
ЛУЧ
Точки, принадлежащие лучу KL
Точки, не принадлежащие лучу KL
A
C
В
K
O
D
L
S
T
Лучи, пересекающие луч KL
Лучи, не пересекающие луч KL
10
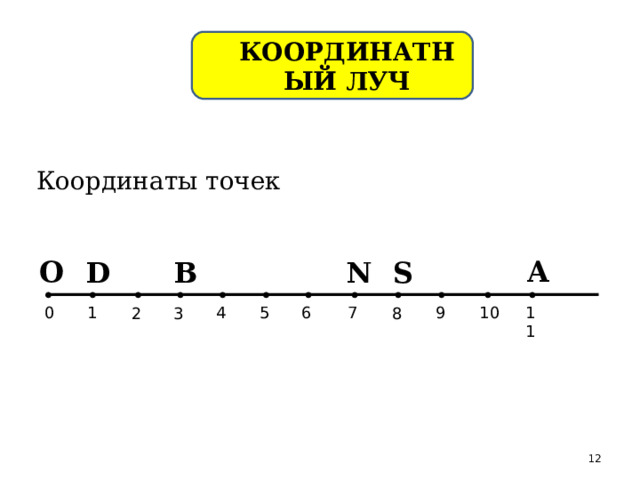
КООРДИНАТНЫЙ ЛУЧ
Координаты точек
A
O
B
N
S
D
5
10
7
6
11
9
1
0
4
8
3
2
11
Тема 2
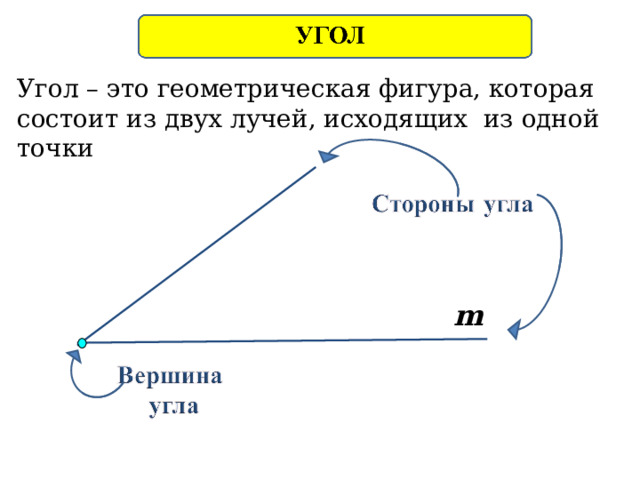
Угол – это геометрическая фигура, которая состоит из двух лучей, исходящих из одной точки
m
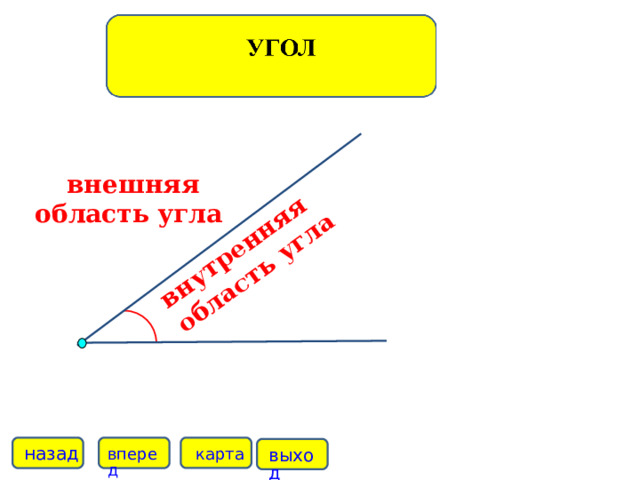
внутренняя
область угла
внешняя
область угла
назад
карта
вперед
выход
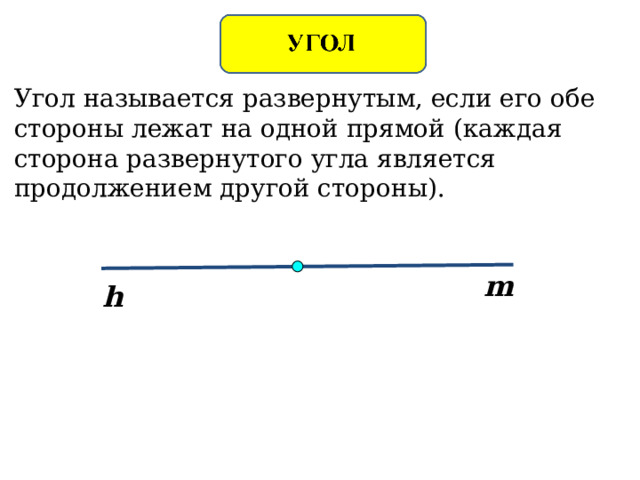
Угол называется развернутым, если его обе стороны лежат на одной прямой ( каждая сторона развернутого угла является продолжением другой стороны).
m
h
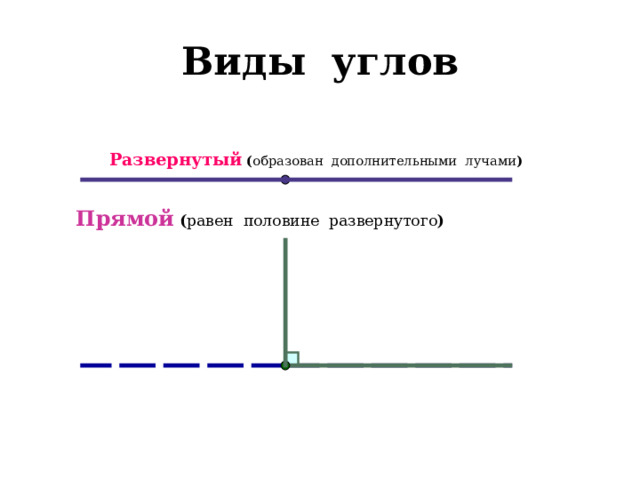
Виды углов
Развернутый ( образован дополнительными лучами )
Прямой ( равен половине развернутого )
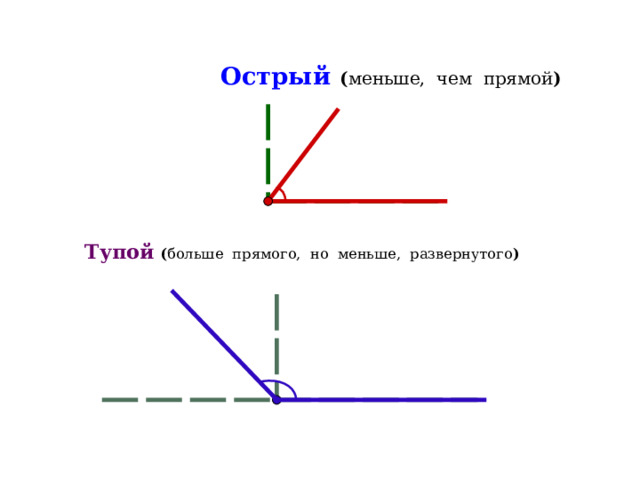
Острый ( меньше, чем прямой )
Тупой ( больше прямого, но меньше, развернутого )
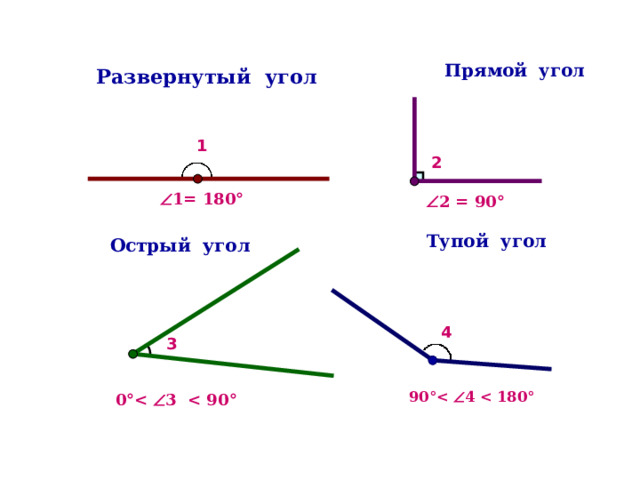
Прямой угол
Развернутый угол
1
2
1= 180 °
2 = 90 °
Тупой угол
Острый угол
4
3
90 ° 4 180 °
0 ° 3 90 °
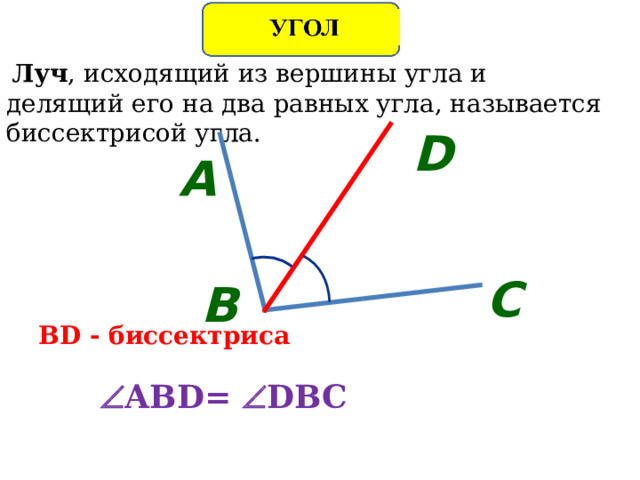
Луч , исходящий из вершины угла и делящий его на два равных угла, называется биссектрисой угла.
D
A
С
B
BD - биссектриса
ABD= DBC
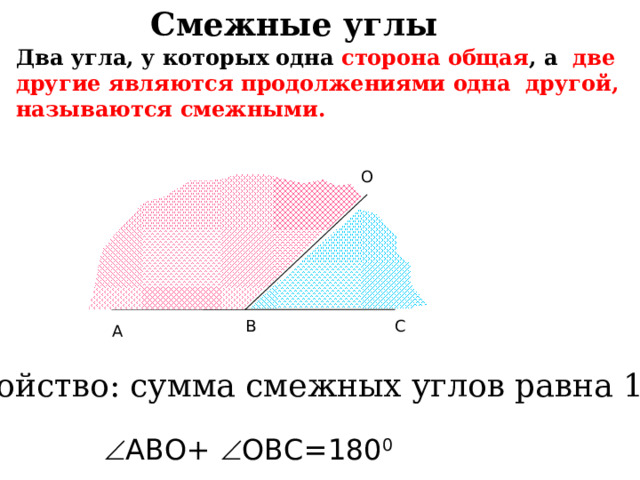
Смежные углы
Два угла, у которых одна сторона общая , а две другие являются продолжениями одна другой, называются смежными.
О
В
С
А
Свойство: сумма смежных углов равна 180 0
АВО+ ОВС=180 0
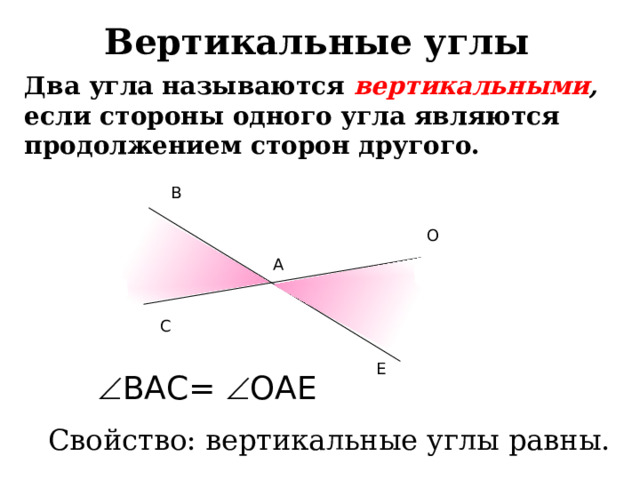
Вертикальные углы
Два угла называются вертикальными , если стороны одного угла являются продолжением сторон другого.
В
О
А
С
Е
ВАС= ОАЕ
Свойство: вертикальные углы равны.
Тема 3
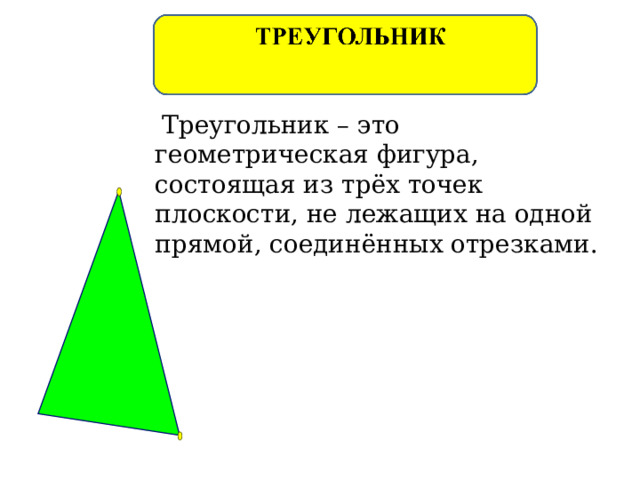
Треугольник – это геометрическая фигура, состоящая из трёх точек плоскости, не лежащих на одной прямой, соединённых отрезками.
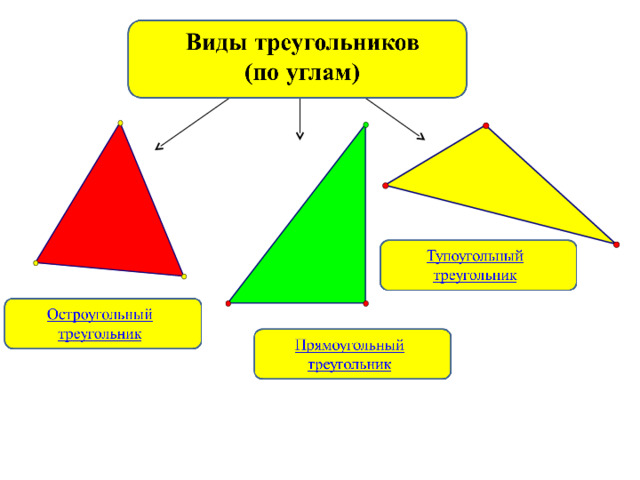
Треугольник, у которого есть прямой угол, называется прямоугольным.
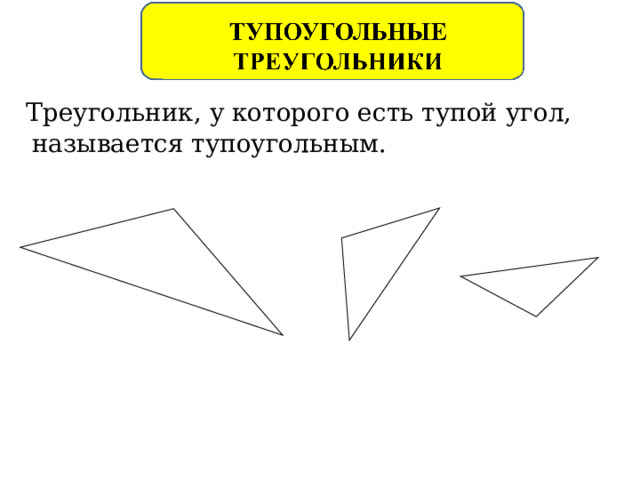
Треугольник, у которого есть тупой угол, называется тупоугольным.
`
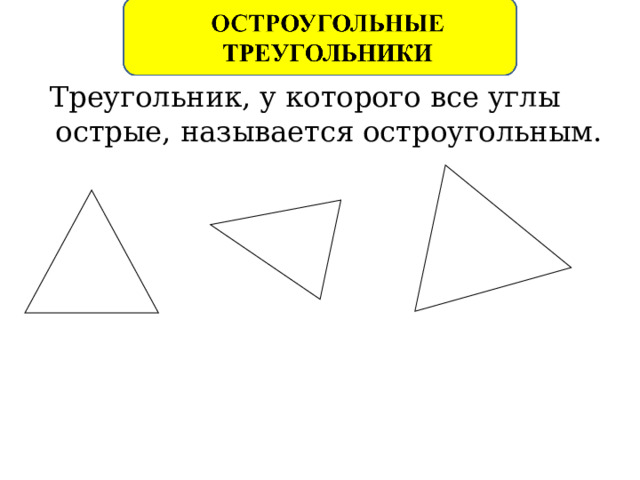
Треугольник, у которого все углы острые, называется остроугольным.
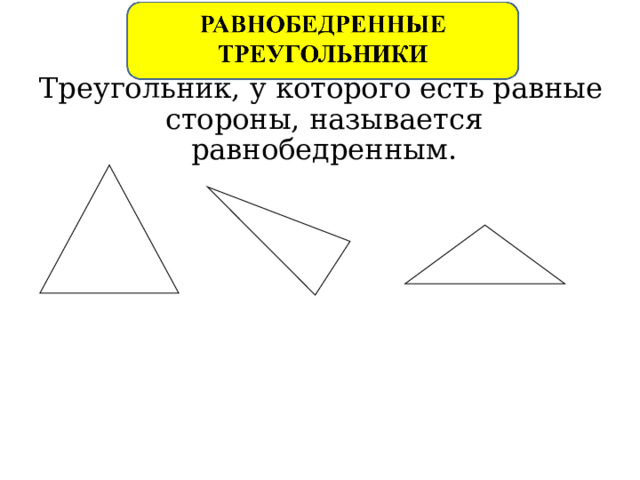
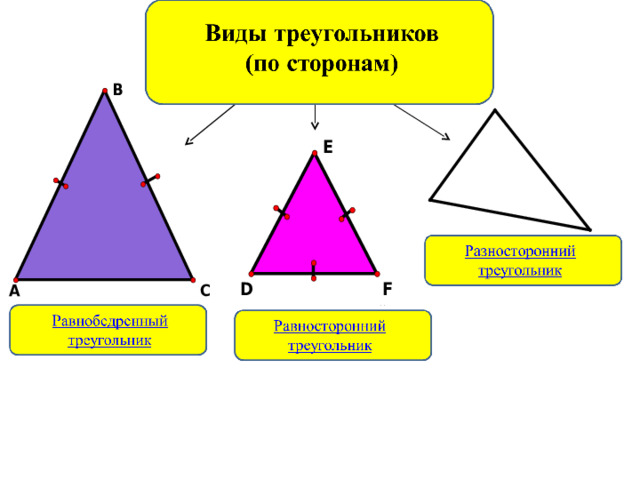
Треугольник, у которого есть равные стороны, называется равнобедренным.
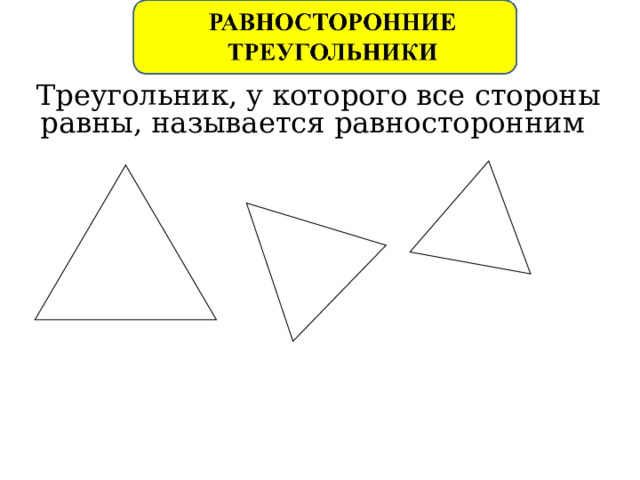
Треугольник, у которого все стороны равны, называется равносторонним
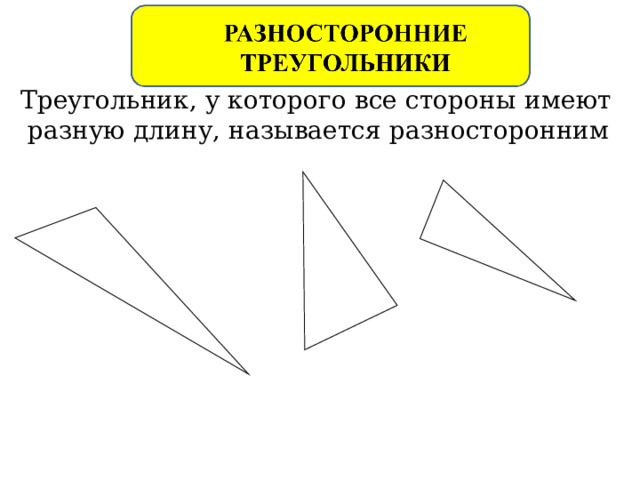
Треугольник, у которого все стороны имеют разную длину, называется разносторонним
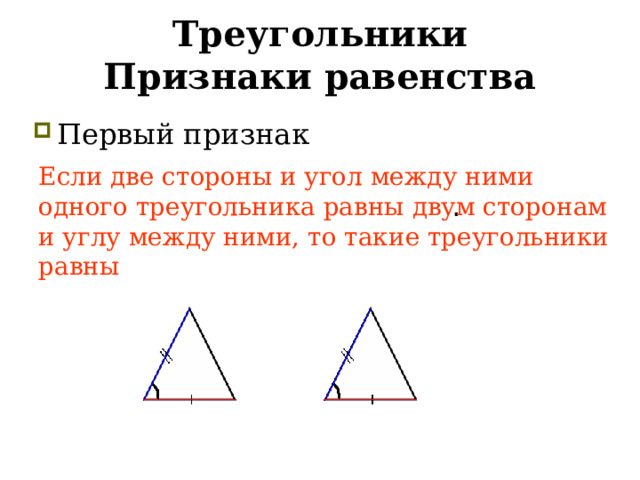
Треугольники Признаки равенства
- Первый признак
две стороны и угол между ними
двум сторонам и углу между ними .
Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними, то такие треугольники равны
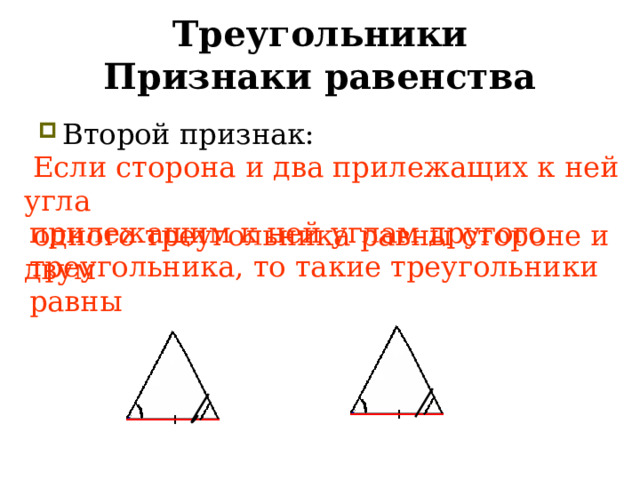
Треугольники Признаки равенства
- Второй признак: торона и два прилежащих к ней угла
Если сторона и два прилежащих к ней угла
одного треугольника равны стороне и двум
прилежащим к ней углам другого треугольника, то такие треугольники равны
Если три стороны одного треугольника равны трем сторонам другого треугольника соответственно, то такие треугольники равны
Треугольники Признаки равенства
- Третий признак
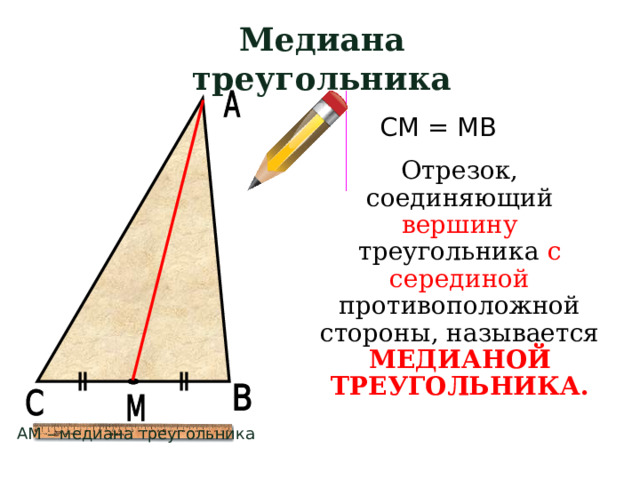
Медиана треугольника
СМ = МВ
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется МЕДИАНОЙ ТРЕУГОЛЬНИКА.
АМ – медиана треугольника
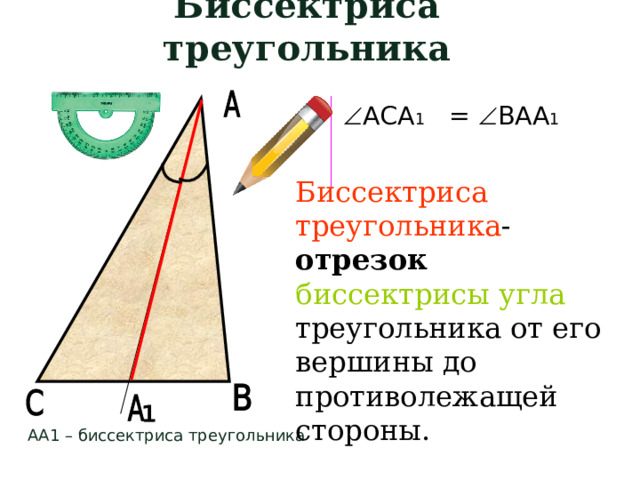
Биссектриса треугольника
АСА 1 = ВАА 1
Биссектриса треугольника - отрезок биссектрисы угла треугольника от его вершины до противолежащей стороны.
АА1 – биссектриса треугольника
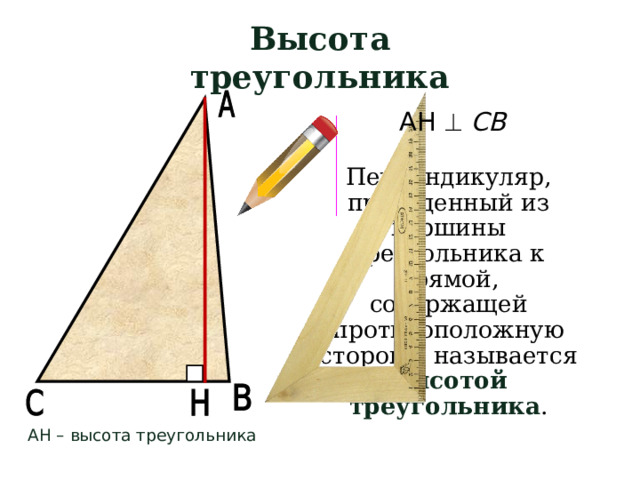
Высота треугольника
АН СВ
Перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника .
АН – высота треугольника
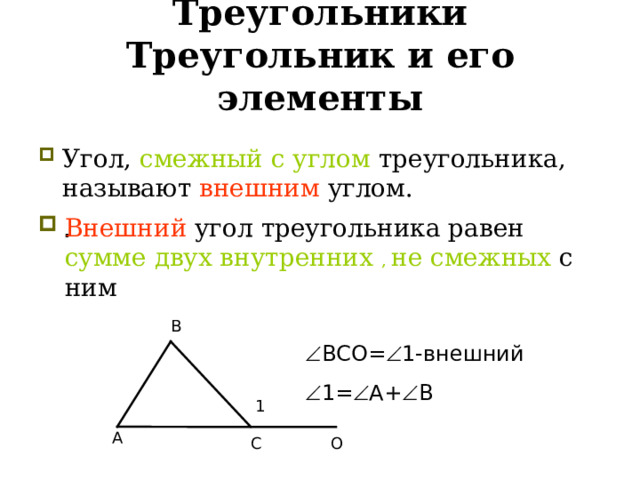
Треугольники Треугольник и его элементы
- Угол, смежный с углом треугольника, называют внешним углом.
- .
Внешний угол треугольника равен сумме двух внутренних , не смежных с ним
В
ВСО= 1-внешний
1= А+ В
1
А
С
О
Неравенство
треугольника
Б о л ь ш а я с т о р о н а
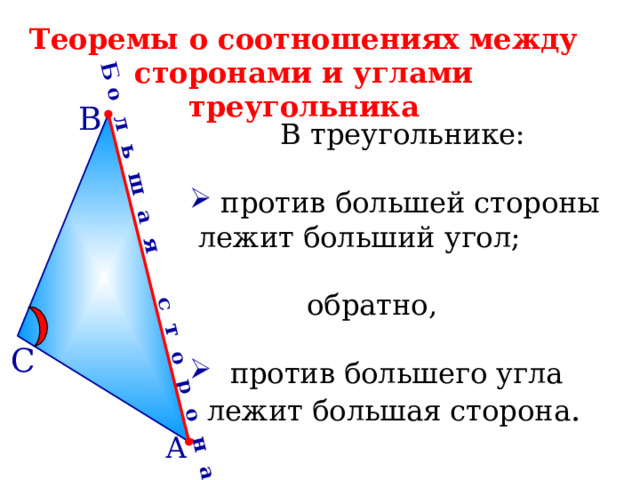
Теоремы о соотношениях между сторонами и углами треугольника
В
В треугольнике:
- против большей стороны
лежит больший угол;
обратно,
- против большего угла
лежит большая сторона .
С
А
AB АВ + А C B С АВ + C В A С А С " width="640"
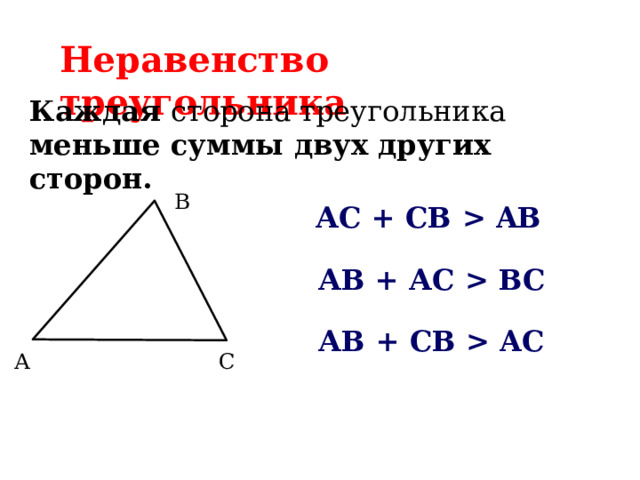
Неравенство треугольника
Каждая сторона треугольника меньше суммы двух других сторон.
В
А C + C В AB
АВ + А C B С
АВ + C В A С
А
С
Тема 4
Прямоугольный треугольник Определение
- Треугольник называется прямоугольным , если один из его углов прямой.
С=90 0
катеты
АС, ВС-
АВ-
гипотенуза
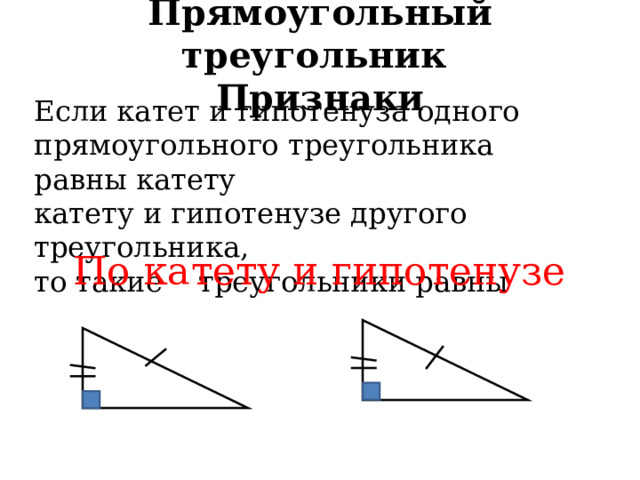
Прямоугольный треугольник Признаки
Если катет и гипотенуза одного прямоугольного треугольника равны катету
катету и гипотенузе другого треугольника,
то такие треугольники равны
По катету и гипотенузе
Прямоугольный треугольник Признаки
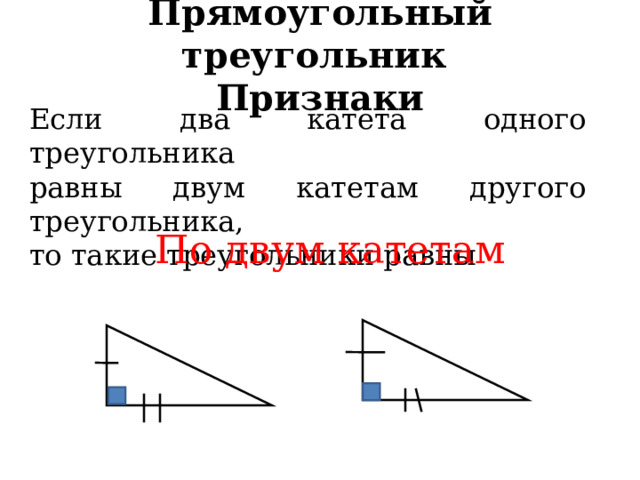
Если два катета одного треугольника
равны двум катетам другого треугольника,
то такие треугольники равны
По двум катетам
Прямоугольный треугольник Признаки
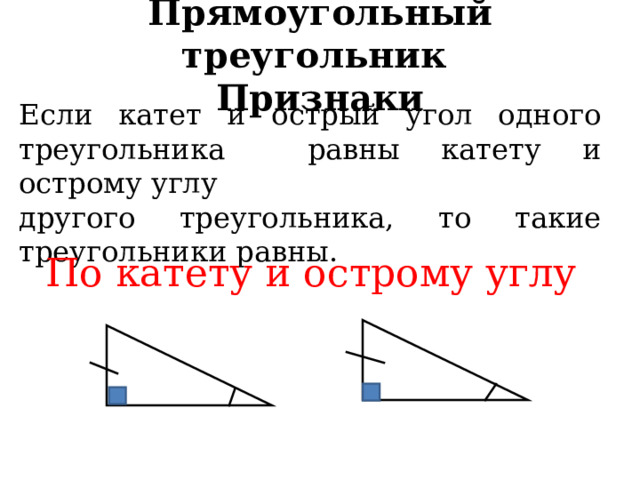
Если катет и острый угол одного треугольника равны катету и острому углу
другого треугольника, то такие треугольники равны.
По катету и острому углу
Прямоугольный треугольник Признаки
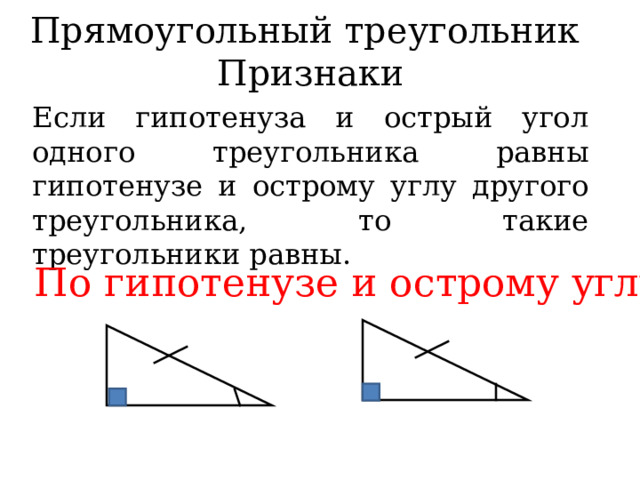
Если гипотенуза и острый угол одного треугольника равны гипотенузе и острому углу другого треугольника, то такие треугольники равны.
По гипотенузе и острому углу
Прямоугольный треугольник Свойства
- Катет прямоугольного треугольника, лежащий против угла 30 0 , равен половине гипотенузы.
А=90 0
С
В=30 0
АС=0,5ВС
А
В
Прямоугольный треугольник Свойства
В прямоугольном треугольнике сумма острых углов равна 90 0 .
С
А=90 0 , В+ С=90 0
В
А
Тема 5
Равнобедренный треугольник Определение
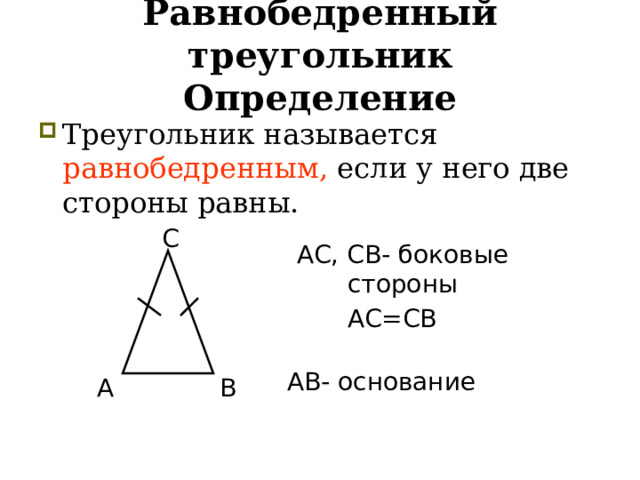
- Треугольник называется равнобедренным, если у него две стороны равны.
С
АС, СВ- боковые стороны
АС=СВ
АВ- основание
А
В
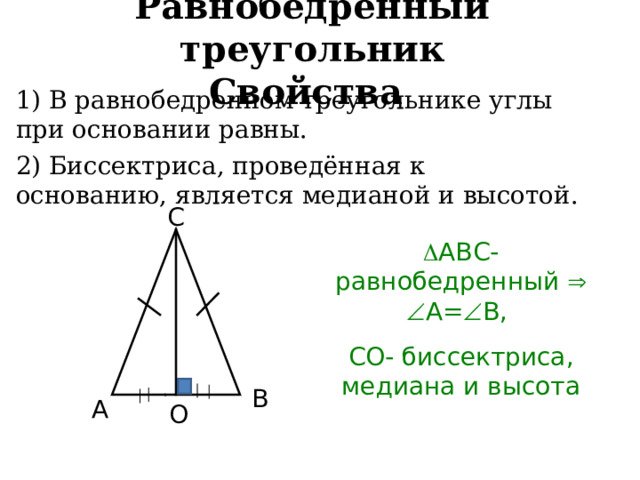
Равнобедренный треугольник Свойства
1) В равнобедренном треугольнике углы при основании равны.
2) Биссектриса, проведённая к основанию, является медианой и высотой.
С
АВС- равнобедренный А= В,
СО- биссектриса, медиана и высота
В
А
О
Равнобедренный треугольник Признаки
- Если в треугольнике два угла равны , то он равнобедренный.
- Если в треугольнике медиана является высотой , то он равнобедренный.
- Если в треугольнике медиана является биссектрисой , то он равнобедренный.
- Если в треугольнике высота является биссектрисой , то он равнобедренный
Тема 6
Параллельные прямые определение
- Прямые называются параллельными, если
-они лежат в одной плоскости
-они не пересекаются
а
b
а b
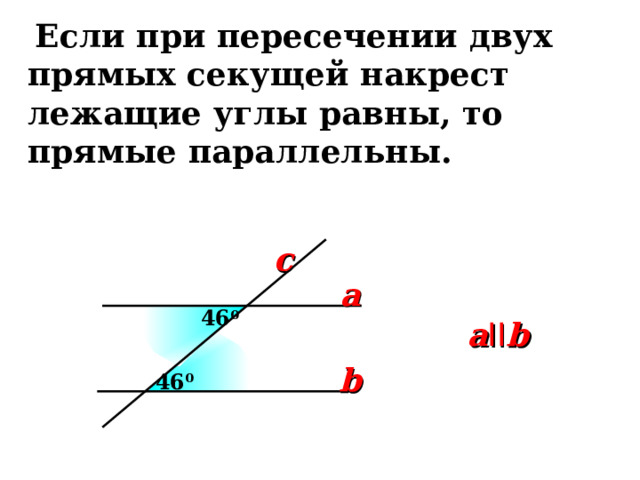
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
c
a
46 0
a II b
b
46 0
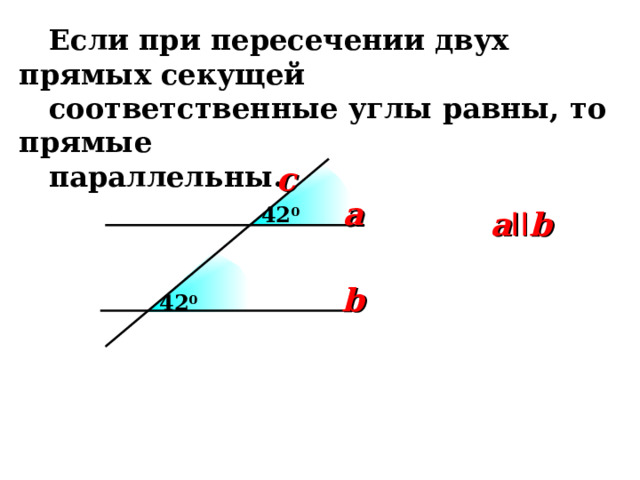
Если при пересечении двух прямых секущей
соответственные углы равны, то прямые
параллельны.
c
a
4 2 0
a II b
b
4 2 0
Если при пересечении двух прямых секущей сумма односторонних углов равна 180 0 , то прямые параллельны.
c
a
a II b
138 0
b
4 2 0
ЕСЛИ
Условие
Заключение
ПРИ ПЕРЕСЕЧЕНИИ ДВУХ ПРЯМЫХ СЕКУЩЕЙ НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ,
ТО
ПРЯМЫЕ ПАРАЛЛЕЛЬНЫ
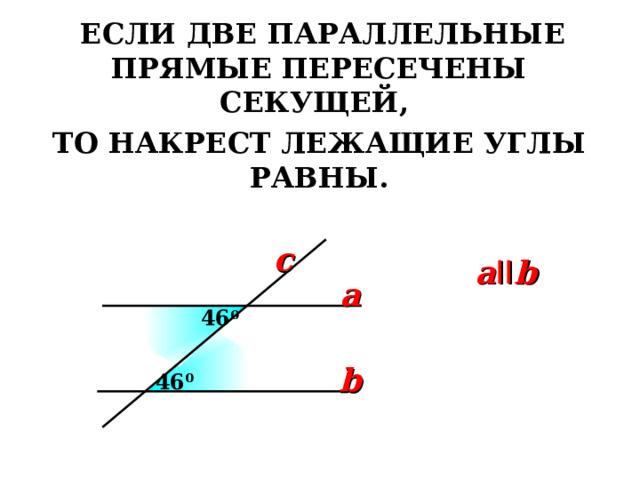
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ,
ТО НАКРЕСТ ЛЕЖАЩИЕ УГЛЫ РАВНЫ.
c
a II b
a
46 0
b
46 0
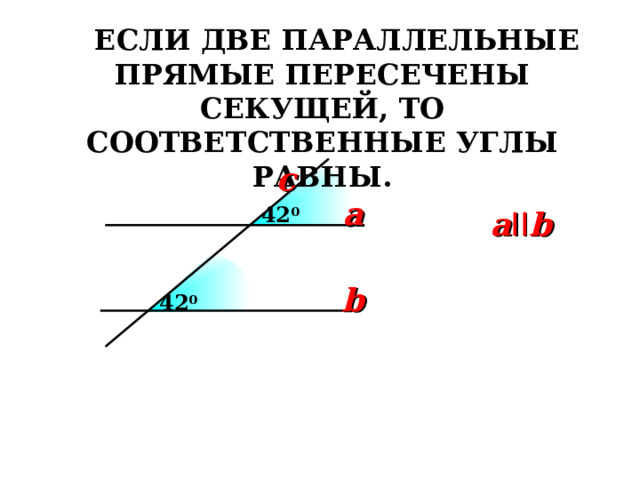
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ, ТО СООТВЕТСТВЕННЫЕ УГЛЫ РАВНЫ.
c
a
4 2 0
a II b
b
4 2 0
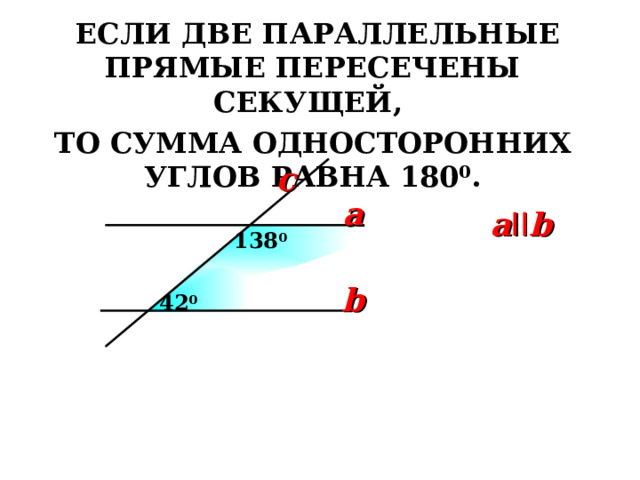
ЕСЛИ ДВЕ ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ ПЕРЕСЕЧЕНЫ СЕКУЩЕЙ,
ТО СУММА ОДНОСТОРОННИХ УГЛОВ РАВНА 180⁰.
c
a
a II b
138 0
b
4 2 0
Тема 7
Аксиома – это
утверждение , принимаемое без доказательства
Теорема – это
утверждение , справедливость которого устанавливается путем рассуждений, т.е. доказательством.
Теорема
У словие З аключение
Обратная теорема
Теоремой, обратной данной называется такая теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы.
Теорема:
Если треугольник равнобедренный, то углы при основании равны.
Теорема, обратная данной:
Если углы треугольника при основании равны, то этот треугольник равнобедренный.
Электронный справочник по геометрии для 7 класса (3.31 MB)
0
735
50
Нравится
0
