Электронный образовательный ресурс "Арифметическая и геометрическая прогрессии"

Арифметическая и геометрическая прогрессии

Урок подготовил :

Зоря Александр Васильевич

учитель математики

http://a-v-zorya.ru

e-mail: [email protected]

Муниципальное бюджетное общеобразовательное учреждение «Октябрьскоготнянская средняя общеобразовательная школа»

станция Кулиновка, Борисовский район, Белгородская область.

http:// октябрьскоготнянская-школа.рф

e-mail: [email protected]

Урок подготовил:

Зоря Александр Васильевич, учитель математики

http://a-v-zorya.ru

e-mail: [email protected]

Муниципальное бюджетное общеобразовательное учреждение «Октябрьскоготнянская средняя общеобразовательная школа»

станция Кулиновка, Борисовский район, Белгородская область.

http://октябрьскоготнянская-школа.рф

e-mail: [email protected]

Цели и задачи урока

Цели урока:

• Образовательные : обобщение и систематизация теоретических знаний учащихся по изученной теме; подготовка к ГИА;
• Развивающие : развитие математического мышления учащихся и вычислительных навыков.
• Воспитательные : содействовать воспитанию интереса к математике и её приложениям.

Тип урока : урок повторения, обобщения и систематизации знаний.

Оборудование : компьютер, мультимедийный проектор, экран, карточки.

Цели урока:

Образовательные: обобщение и систематизация теоретических знаний учащихся по изученной теме; подготовка к ГИА;

Развивающие: развитие математического мышления учащихся и вычислительных навыков.

Воспитательные: содействовать воспитанию интереса к математике и её приложениям.

Тип урока: урок повторения, обобщения и систематизации знаний.

Оборудование: компьютер, мультимедийный проектор, экран, карточки

Арифметическая и геометрическая прогрессии

Сегодня пред последний урок по главе “Арифметическая и геометрическая прогрессии”. Перед вами задача - показать, как вы знаете формулы прогрессии и умеете их применять при решении различных задач.

На столах лежат задания к уроку, ваша цель внимательно работать на уроке и по ходу урока заполнить таблицу:

Алгебра 9 класс

Арифметическая и геометрическая прогрессии

Лист самооценки

Этап

Оценка

Проверка знаний формул

Устная работа

Работа по карточкам

Самостоятельная работа

Помощь с места

ИТОГО:

Лист самооценки. За каждый правильный ответ при опросе и за участие на различных этапах урока ставьте один плюс. «5» - более 9 плюсов

«4» - от 5 до 8 плюсов

менее 5 плюсов – оценку не заработал. (шкала может варьироваться)

За каждый правильный ответ при опросе и за участие на различных этапах урока ставьте один плюс.

«5» - более 9 плюсов

«4» - от 5 до 8 плюсов

менее 5 плюсов – оценку не заработал

Арифметическая и геометрическая прогрессии

Эпиграф урока

«Д о роги не те знания, которые откладываются в мозгу, как жир, д о роги те, которые превращаются в умственные мышцы».

(Герберт Спенсер, английский философ)

Эпиграф урока

«Д о роги не те знания, которые откладываются в мозгу, как жир, д о роги те, которые превращаются в умственные мышцы».

(Герберт Спенсер, английский философ)

Арифметическая и геометрическая прогрессии

Тестирование

Тест по формулам

Вспомните формулы по теме «Арифметическая и геометрическая прогрессия» и в тесте соотнесите формулу с её описанием.

Нажать на прямоугольник для запуска теста. После завершения тестирования закройте окно теста.

За каждый верный ответ в Лист самооценки ставится «+».

Завершить работу с тестом

Кнопка завершения работы с тестом появится через 20 секунд

Если тест не запустится, то на левой области экрана нажмите правую кнопку мыши и в меню Adobe Flash Player выберите пункт «Воспроизвести»

Арифметическая и геометрическая прогрессии

Устная работа

Определите вид числовой последовательности

1) 2; 5; 8; 11; 14; 17;…

2) 3; 9; 27; 81; 243;…

3) 1; 6; 11; 20; 25;…

4) - 4; - 8; -16; - 32; …

5) 5; 25; 35; 45; 55;…

6) - 2; - 4; - 6; - 8; …

Начать тест

Задача

Определите какая последовательность является арифметической или геометрической прогрессией, найдите, соответственно, разность и знаменатель, при проверке повторить определение прогрессий.

• Дайте определение арифметической прогрессии.
• Какой буквой обозначают разность арифметической прогрессии?
• Что означает разность арифметической прогрессии?
• Дайте определение геометрической прогрессии.
• Какой буквой обозначают знаменатель геометрической прогрессии?
• Что означает разность геометрической прогрессии?
• Какая прогрессия называется возрастающей?
• Какая прогрессия называется убывающей?

Проверка ответа происходит при нажатии на прямоугольник со стрелкой. Нажатие на пустое место экрана выводит «вопросительный знак» подсказка в соответствии с заданием со страниц учебника.

За каждый верный ответ в Лист самооценки ставится «+».

1) 2; 5; 8; 11; 14; 17;…

2) 3; 9; 27; 81; 243;…

3) 1; 6; 11; 20; 25;…

4) - 4; - 8; -16; - 32; …

5) 5; 25; 35; 45; 55;…

6) - 2; - 4; - 6; - 8; …

Задача

Если тест не запустится, то на левой области экрана нажмите правую кнопку мыши и в меню Adobe Flash Player выберите пункт «Воспроизвести»

Нажатие на вопросительный знак перенаправляет на правило из учебника

Определите какая последовательность является арифметической или геометрической прогрессией, найдите, соответственно, разность и знаменатель, при проверке повторить определение прогрессий.

• Дайте определение арифметической прогрессии.
• Какой буквой обозначают разность арифметической прогрессии?
• Что означает разность арифметической прогрессии?
• Дайте определение геометрической прогрессии.
• Какой буквой обозначают знаменатель геометрической прогрессии?
• Что означает разность геометрической прогрессии?
• Какая прогрессия называется возрастающей?
• Какая прогрессия называется убывающей?

Проверка ответа происходит при нажатии на прямоугольник со стрелкой. Нажатие на пустое место экрана выводит «вопросительный знак» подсказка в соответствии с заданием со страниц учебника.

За каждый верный ответ в Лист самооценки ставится «+».

Арифметическая и геометрическая прогрессии

Назад, в историю!

На связь между прогрессиями первым обратил внимание великий АРХИМЕД (ок. 287–212 гг. до н.э.)

Термин «прогрессия» был введён римским автором Боэцием (в 6 веке) и понимался в более широком смысле, как бесконечная числовая последовательность. В переводе с латинского, слово progressio означает «движение вперёд». Названия «арифметическая» и «геометрическая» были перенесены из теории непрерывных пропорций, которыми занимались древние греки.

Формула суммы членов арифметической прогрессии была доказана древнегреческим учёным Диофантом (в 3 веке). Формула суммы членов геометрической прогрессии дана в книге Евклида «Начала» (3 век до н.э.).

Правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в сочинении «Книги абака» в 1202г. (Леонардо Пизанский)

А общее правило для суммирования любой конечной геометрической прогрессии встречается в книге Никола Шюке «Наука о числах», увидевшей свет в 1484 году.

Назад в историю.

На связь между прогрессиями первым обратил внимание великий АРХИМЕД (ок. 287–212 гг. до н.э.)

Термин «прогрессия» был введён римским автором Боэцием (в 6 веке) и понимался в более широком смысле, как бесконечная числовая последовательность. В переводе с латинского, слово progressio означает «движение вперёд». Названия «арифметическая» и «геометрическая» были перенесены из теории непрерывных пропорций, которыми занимались древние греки.

Формула суммы членов арифметической прогрессии была доказана древнегреческим учёным Диофантом (в 3 веке). Формула суммы членов геометрической прогрессии дана в книге Евклида «Начала» (3 век до н.э.).

Правило для нахождения суммы членов произвольной арифметической прогрессии впервые встречается в сочинении «Книги абака» в 1202г. (Леонардо Пизанский)

А общее правило для суммирования любой конечной геометрической прогрессии встречается в книге Никола Шюке «Наука о числах», увидевшей свет в 1484 году.

Арифметическая и геометрическая прогрессии

Работа у доски

2) Дано: ( b n ) геометрическая прогрессия

1) Дано: ( а n ) арифметическая прогрессия

а 1 = 5, d = 3

b 1 = 5, q = 3

Найти: а 6 ; а 10 ?

Найти: b 3 ; b 5 ?

3) Дано: ( а n ) арифметическая прогрессия

4) Дано: ( b n ) геометрическая прогрессия

а 4 = 11, d = 2

b 4 = 40, q = 2

Найти: а 1 ?

Найти: b 1 ?

Работа у доски.

В тетрадях запишите сегодняшнее число, тема урока «Арифметическая и геометрическая прогрессия», «Классная работа».

Четыре ученика выходят к доске и решают по одному заданию на свой выбор. Остальные решают на местах. Карточки с заданиями прилагаются.

При нажатии на каждое из заданий откроется слайд с решением задания (слайды 25-28), возврат из которого происходит при нажатии на соответствующую кнопку.

За каждое верное решение и комментарий решения в Лист самооценки ставится «+».

1)Дано: ( а n ) арифметическая прогрессия

а 1 = 5, d = 3

Найти: а 6 ; а 10 ?

2)Дано: ( b n ) геометрическая прогрессия

b 1 = 5, q = 3

Найти: b 3 ; b 5 ?

3)Дано: ( а n ) арифметическая прогрессия

а 4 = 11, d = 2

Найти: а 1 ?

4)Дано: ( b n ) геометрическая прогрессия

b 4 = 40, q = 2

Найти: b 1 ?

Арифметическая и геометрическая прогрессии

Физкультминутка

Физкультминутка.

Нажать на смайлик для начала физкультминутки.

Продолжение - слайд 33

Арифметическая и геометрическая прогрессии

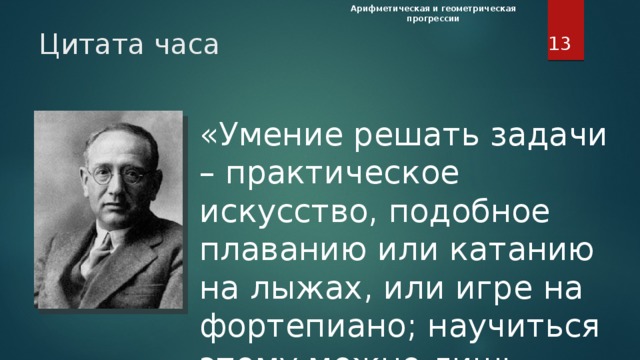
Цитата часа

«Умение решать задачи – практическое искусство, подобное плаванию или катанию на лыжах, или игре на фортепиано; научиться этому можно лишь подражая избранным образцам и постоянно тренируясь».

(Дьёрдь Пойа, швейцарский математик)

Цитата часа.

«Умение решать задачи – практическое искусство, подобное плаванию или катанию на лыжах, или игре на фортепиано; научиться этому можно лишь подражая избранным образцам и постоянно тренируясь».

(Дьёрдь Пойа, швейцарский математик)

Только самостоятельно решая задачи вы научитесь их решать

Арифметическая и геометрическая прогрессии

Характерное свойство арифметической прогрессии

Дано: ( а n ) арифметическая прогрессия

а 4 =12,5 ; а 6 =17,5

Найти: а 5 ?

используя свойство

Решение

арифметической прогрессии имеем:

Характерное свойство арифметической прогрессии. При нажатии на «вопросительный знак» выводится правило из учебника. Ученики должны записать образец решения себе в тетрадь.

Дано: ( а n ) арифметическая прогрессия

а 4 =12,5 ; а 6 =17,5

Найти: а 5 ?

Ответ: 15

0 b 4 =6; b 6 =24 Найти: b 5 ?   используя свойство Решение геометрической прогрессии имеем: Характерное свойство геометрической прогрессии. При нажатии на «вопросительный знак» выводится правило из учебника. Ученики должны записать образец решения себе в тетрадь. Дано: ( b n ) геометрическая прогрессия , b n 0 b 4 =6; b 6 =24 Найти: b 5 ?   Ответ: 12" width="640"

Арифметическая и геометрическая прогрессии

Характерное свойство геометрической прогрессии

Дано: ( b n ) геометрическая прогрессия , b n 0

b 4 =6; b 6 =24

Найти: b 5 ?

используя свойство

Решение

геометрической прогрессии имеем:

Характерное свойство геометрической прогрессии. При нажатии на «вопросительный знак» выводится правило из учебника. Ученики должны записать образец решения себе в тетрадь.

Дано: ( b n ) геометрическая прогрессия , b n 0

b 4 =6; b 6 =24

Найти: b 5 ?

Ответ: 12

Арифметическая и геометрическая прогрессии

5 3 1 3

02 МАТЕМАТ

204310 9

0 7 2 1

ЗОРЯ

АЛЕКСАНДР

ВАСИЛЬЕВИЧ

При решении самостоятельной работы следует ответы на задания перенести в бланк ответов №1 ГИА. Рекомендуется в начале объяснить и повторить правила заполнения бланка.

0, b 2 = 4, b 4 = 9. Найти: b 3 – ? 5) Дано: ( а n ), а 1 = 28, а 21 = 4. Найти: d – ? 6) Дано: ( b n ), b 1 =1/2, q = 2 . Найти: b 5 – ? 7) Дано: ( а n ), а 7 = 16, а 9 = 30. Найти: а 8 – ? Самостоятельная работа. Задания на печатных карточках у учащихся. 1) Дано: ( а n ), а 1 = - 3, а 2 = 4. Найти: а 16 – ? 2) Дано: ( b n ), b 12 = - 32, b 13 = - 16. Найти: q – ? 3) Дано: ( а n ), а 21 = - 44, а 22 = - 42. Найти: d – ? 4) Дано: ( b n ), b п 0, b 2 = 4, b 4 = 9. Найти: b 3 – ? 5) Дано: ( а n ), а 1 = 28, а 21 = 4. Найти: d – ? 6) Дано: ( b n ), b 1 =1/2, q = 2 . Найти: b 5 – ? 7) Дано: ( а n ), а 7 = 16, а 9 = 30. Найти: а 8 – ?" width="640"

Арифметическая и геометрическая прогрессии

Самостоятельная работа

1) Дано: ( а n ), а 1 = - 3, а 2 = 4. Найти: а 16 – ?

2) Дано: ( b n ), b 12 = - 32, b 13 = - 16. Найти: q – ?

3) Дано: ( а n ), а 21 = - 44, а 22 = - 42. Найти: d – ?

4) Дано: ( b n ), b п 0, b 2 = 4, b 4 = 9. Найти: b 3 – ?

5) Дано: ( а n ), а 1 = 28, а 21 = 4. Найти: d – ?

6) Дано: ( b n ), b 1 =1/2, q = 2 . Найти: b 5 – ?

7) Дано: ( а n ), а 7 = 16, а 9 = 30. Найти: а 8 – ?

Самостоятельная работа.

Задания на печатных карточках у учащихся.

1) Дано: ( а n ), а 1 = - 3, а 2 = 4. Найти: а 16 – ?

2) Дано: ( b n ), b 12 = - 32, b 13 = - 16. Найти: q – ?

3) Дано: ( а n ), а 21 = - 44, а 22 = - 42. Найти: d – ?

4) Дано: ( b n ), b п 0, b 2 = 4, b 4 = 9. Найти: b 3 – ?

5) Дано: ( а n ), а 1 = 28, а 21 = 4. Найти: d – ?

6) Дано: ( b n ), b 1 =1/2, q = 2 . Найти: b 5 – ?

7) Дано: ( а n ), а 7 = 16, а 9 = 30. Найти: а 8 – ?

Арифметическая и геометрическая прогрессии

5 3 1 3

02 МАТЕМАТ

204310 9

0 7 2 1

ЗОРЯ

АЛЕКСАНДР

ВАСИЛЬЕВИЧ

1 0 2

0 , 5

Самостоятельная работа.

По истечении отведённого на работу времени учащиеся обмениваются бланками ответов и проводят поверку в соответствии с образцом на слайде. Каждое верное решение – «+» в Лист самооценки.

2

6

- 1 , 2

8

2 3

Арифметическая и геометрическая прогрессии

Интересные факты

1) Химия. При повышении температуры по арифметической прогрессии скорость химических реакций растёт по геометрической прогрессии.

2) Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию.

3) Физика. И в физических процессах встречается эта закономерность. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их ещё на 4 части и т.д. – это геометрическая прогрессия.

4) Биология. Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, через одинаковый промежуток времени их число удваивается.

5) Экономика. Вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии, сложные проценты – увеличение в геометрической прогрессии.

Интересные факты из практического применения арифметической и геометрической прогрессии.

Учащиеся с места читают по одному факту.

1) Химия. При повышении температуры по арифметической прогрессии скорость химических реакций растёт по геометрической прогрессии.

2) Геометрия. Вписанные друг в друга правильные треугольники образуют геометрическую прогрессию.

3) Физика. И в физических процессах встречается эта закономерность. Нейтрон, ударяя по ядру урана, раскалывает его на две части. Получаются два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывает их ещё на 4 части и т.д. – это геометрическая прогрессия.

4) Биология. Микроорганизмы размножаются делением пополам, поэтому при благоприятных условиях, через одинаковый промежуток времени их число удваивается.

5) Экономика. Вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии, сложные проценты – увеличение в геометрической прогрессии.

Арифметическая и геометрическая прогрессии

Домашнее задание из сборника ГИА

6.1. 1) Пятый член арифметической прогрессии равен 8,4 , а её десятый член равен 14,4. Найдите пятнадцатый член этой прогрессии.

6.2. 1) Число -3,8 является восьмым членом арифметической прогрессии ( а п ) , а число -11 является её двенадцатым членом. Является ли членом этой прогрессии число -30,8 ?

6.5. 1) Между числами 6 и 17 вставьте четыре числа так, чтобы вместе с данными числами они образовали арифметическую прогрессию.

6.8. 1) В геометрической прогрессии b 12 = З 15 и b 14 = З 17 . Найдите b 1 .

Домашнее задание. Из сборника ГИА 6.1, 6.2, 6.5, 6.8.

Используя оценочные листы, подводятся итоги работы на уроке. Объявляются оценки.

Арифметическая и геометрическая прогрессии

Рефлексивный экран

Выберите любое начало фразы и закончите её

сегодня я узнал…

было интересно…

я приобрёл…

я научился…

было трудно…

я выполнял задания…

у меня получилось …

я смог…

я понял, что…

теперь я могу…

я попробую…

меня удивило…

я почувствовал, что…

урок дал мне для жизни…

мне захотелось…

Рефлексивный экран.

Обычно в конце урока подводятся его итоги,  обсуждение того, что узнали, и того, как работали – т.е. каждый оценивает свой вклад в достижение поставленных в начале урока целей, свою активность. Ребята по кругу высказываются одним предложением, выбирая начало фразы из рефлексивного экрана на доске

сегодня я узнал…

было интересно…

было трудно…

я выполнял задания…

я понял, что…

теперь я могу…

я почувствовал, что…

я приобрёл…

я научился…

у меня получилось …

я смог…

я попробую…

меня удивило…

урок дал мне для жизни…

мне захотелось…

Арифметическая и геометрическая прогрессии

Урок сегодня завершён,

Но каждый должен знать:

Познание, упорство, труд

К прогрессу в жизни приведут!

Завершение урока.

Урок сегодня завершён,

Но каждый должен знать:

Познание, упорство, труд

К прогрессу в жизни приведут!

Арифметическая и геометрическая прогрессии

Спасибо за урок!

Урок окончен. Спасибо за урок!

Смена данного и последующих слайдов происходит автоматически.

Используемые источники и ПО

• Алгебра. 9 класс : учеб. Для общеобразоват. учреждений / [Макарычев Ю.Н., Миндюк Г.Н., Нешков К.И., Суворова С.Б.] ; под ред. Теляковского С.А. – 16-е изд. – М. : Просвещение, 2009. – 271 с. : ил.
• Канина Г. В., учитель математики. Урок-презентация «Арифметическая и геометрическая прогрессия» [Электронный ресурс] – URL: http://festival.1september.ru/articles/534291/ (27.02.2013).
• Мелом пишут по доске [Звук] – URL: http://zvuki-tut.narod.ru/melom_pishut_po_doske/Melom_pishut_po_doske.mp3 (28.02.2012).
• Пойа Д. [Картинка] – URL: http://www.apm.pt/pic/_polya_5252dffc9e0eb.jpg (28.02.2013).
• Спенсер Г. [Картинка] – URL: http://upload.wikimedia.org/wikipedia/commons/thumb/9/96/Herbert_Spencer.jpg/389px-Herbert_Spencer.jpg (28.02.2013).
• Шалкина С. В., учитель математики. Здоровьесберегающие технологии на уроках математики [Электронный ресурс] – URL: http://festival.1september.ru/articles/311946/ (01.03.2013).
• iSpring Presenter 7 - разработка тестов и преобразование во flash.
• MS PowerPoint 2010 - разработка презентации.

Используемые источники и программное обеспечение

Алгебра. 9 класс : учеб. Для общеобразоват. учреждений / [Макарычев Ю.Н., Миндюк Г.Н., Нешков К.И., Суворова С.Б.] ; под ред. Теляковского С.А. – 16-е изд. – М. : Просвещение, 2009. – 271 с. : ил.

Канина Г. В., учитель математики. Урок-презентация «Арифметическая и геометрическая прогрессия» [Электронный ресурс] – URL: http://festival.1september.ru/articles/534291/ (27.02.2013).

Мелом пишут по доске [Звук] – URL: http://zvuki-tut.narod2.ru/melom_pishut_po_doske/Melom_pishut_po_doske.mp3 (28.02.2012).

Пойа Д. [Картинка] – URL: http://trvscience.ru/uploads/32N_19.jpg (28.02.2013).

Спенсер Г. [Картинка] – URL: http://upload.wikimedia.org/wikipedia/commons/thumb/9/96/Herbert_Spencer.jpg/389px-Herbert_Spencer.jpg (28.02.2013).

Шалкина С. В., учитель математики. Здоровьесберегающие технологии на уроках математики [Электронный ресурс] – URL: http://festival.1september.ru/articles/311946/ (01.03.2013).

iSpring Suite 6.2.0 - разработка тестов и преобразование во flash.

MS PowerPoint 2013 - разработка презентации.

Арифметическая и геометрическая прогрессии

Работа у доски. Задание 1

1) Дано: ( а n ) арифметическая прогрессия

а 1 = 5, d = 3.

Найти: а 6 ; а 10 ?

используя формулу а n = а 1 + d . (n 1)

Решение

а 6 = а 1 + d . (6 1) = а 1 + 5d = 5 + 5 . 3 = 20;

Работа у доски. Задание 1

1) Дано: ( а n ) арифметическая прогрессия

а 1 = 5, d = 3.

Найти: а 6 ; а 10 ?

Решение: используя формулу а n = а 1 + d . (n -1)

а 6 = а 1 + d . (6-1) = а 1 + 5d = 5 + 5 . 3 = 20

а 10 = а 1 + d . (10-1) = а 1 + 9d = 5 + 9 . 3 = 32

Ответ: 20; 32.

Ответ: 20; 32.

Арифметическая и геометрическая прогрессии

Работа у доски. Задание 2

2) Дано: ( b n ) геометрическая прогрессия

b 1 = 5, q = 3.

Найти: b 3 ; b 5 ?

используя формулу b n = b 1 q n-1

Решение

b 3 = b 1 . q 2 = 5 . 3 2 = 5 . 9 = 4 5;

Работа у доски. Задание 2

2) Дано: ( b n ) геометрическая прогрессия

b 1 = 5, q = 3.

Найти: b 3 ; b 5 ?

Решение: используя формулу b n = b 1 q n-1

b 3 = b 1 . q 2 = 5 . 3 2 = 5 . 9 = 4 5

b 5 = b 1 . q 4 = 5 . 3 4 = 5 . 81 = 405

Ответ: 45; 405.

Ответ: 45; 405.

Арифметическая и геометрическая прогрессии

Работа у доски. Задание 3

3) Дано: ( а n ) арифметическая прогрессия

а 4 = 11, d = 2.

Найти: а 1 ?

используя формулу а n = а 1 + d . (n 1)

Решение

а 4 = а 1 + d . (4 1); а 4 = а 1 + 3d;

Работа у доски. Задание 3

3) Дано: ( а n ) арифметическая прогрессия

а 4 = 11, d = 2.

Найти: а 1 ?

Решение: используя формулу а n = а 1 + d . (n - 1)

а 4 = а 1 + d . (4 - 1); а 4 = а 1 + 3d;

а 1 = а 4 - 3d = 11 - 3 . 2 = 5

Ответ: 5.

Ответ: 5.

Арифметическая и геометрическая прогрессии

Работа у доски. Задание 4

4) Дано: ( b n ) геометрическая прогрессия

b 4 = 40, q = 2.

Найти: b 1 ?

используя формулу b n = b 1 q n-1

Решение

b 4 =b 1 q 4-1 ; b 4 =b 1 q 3 ;

Работа у доски. Задание 4

4) Дано: ( b n ) геометрическая прогрессия

b 4 = 40, q = 2.

Найти: b 1 ?

Решение: используя формулу b n = b 1 q n-1

b 4 =b 1 q 4-1 ; b 4 =b 1 q 3

b 1 = b 4 : q 3 = 40 : 2 3 = 40 : 8 = 5

Ответ: 5.

Ответ: 5.

Арифметическая и геометрическая прогрессии

Определение арифм. прогр.

«Кликните» на слайд для возврата на предыдущий слайд.

Определение арифметической прогрессии

Арифметическая и геометрическая прогрессии

Свойство арифм. прогр.

«Кликните» на слайд для возврата на предыдущий слайд.

Свойство арифметической прогрессии

Арифметическая и геометрическая прогрессии

Определение геометр. прогр.

«Кликните» на слайд для возврата на предыдущий слайд.

Определение геометрической прогрессии

Арифметическая и геометрическая прогрессии

Свойство геометр. прогр.

«Кликните» на слайд для возврата на предыдущий слайд.

Свойство геометрической прогрессии

Арифметическая и геометрическая прогрессии

Гимнастика для глаз, вверх-вниз

Гимнастика для глаз.

Голову держите прямо, не запрокидывайте.

Мягко переводите глаза вверх и вниз 4 раза. Глаза должны двигаться медленно и с равными интервалами. Не прилагайте никаких усилий, используйте минимум силы.

Арифметическая и геометрическая прогрессии

Гимнастика для глаз, влево-вправо

Двигайте глазами из стороны в сторону с максимальной амплитудой, не прилагая усилий 4 раза.

Арифметическая и геометрическая прогрессии

Гимнастика для глаз, диагональ

Взгляните в левый верхний угол, а затем переведите взгляд в правый нижний. Повторите 4 раза. Затем сделайте 4 раза движение глазами из правого верхнего угла в левый нижний

Арифметическая и геометрическая прогрессии

Гимнастика для глаз, овал

Двигайте глазами медленно и мягко по овалу в одну сторону, затем в другую, по 4 круга в каждом направлении.

Арифметическая и геометрическая прогрессии

Гимнастика для глаз, восьмёрка

А сейчас глазами плавно опишите горизонтальную восьмёрку, или же символ бесконечности, максимального размера в пределах лица. В одну сторону 4 раза, а после чего в другую 4 раза. 

Арифметическая и геометрическая прогрессии

Гимнастика для глаз, моргание

Поморгайте часто-часто, легко-легко 4 секунды.

Кликнуть на слайде «белок», чтобы поморгало

Арифметическая и геометрическая прогрессии

Гимнастика для тела

(Одна прямая рука вверх, другая вниз, рывком менять руки).

Вверх рука и вниз рука.

Потянули их слегка.

Быстро поменяли руки!

Нам сегодня не до скуки.

(Вращение головой вправо и влево).

Крутим-вертим головой,

Разминаем шею. Стой! 

(Ходьба на месте, высоко поднимая колени).

И на месте мы шагаем,

Ноги выше поднимаем. 

(Потягивания – руки вверх, в стороны, вперёд).

Потянулись, растянулись

Вверх и в стороны, вперёд. 

(Садимся за парты).

И за парты все вернулись –

Вновь урок у нас идёт. 

Гимнастика для тела.

Нажмите на смайлик для возвращения к уроку

Вверх рука и вниз рука. Потянули их слегка. Быстро поменяли руки! Нам сегодня не до скуки. (Одна прямая рука вверх, другая вниз, рывком менять руки). Крутим-вертим головой, Разминаем шею. Стой!  (Вращение головой вправо и влево). И на месте мы шагаем, Ноги выше поднимаем.  (Ходьба на месте, высоко поднимая колени). Потянулись, растянулись Вверх и в стороны, вперёд.  (Потягивания – руки вверх, в стороны, вперёд). И за парты все вернулись – Вновь урок у нас идёт.  (Садимся за парты).

Нажмите на смайлик для возвращения к уроку

Возвращение на слайд 13