Быстрый счет МБОУ СОШ с. Тунгор

Быстрый счет

МБОУ СОШ с. Тунгор

Учащиеся:

Стожко Алексей, 6 класс

Сбытова Ирина, 5 класс

Учитель: Филонов Л.Н.

Девиз: незнающие пусть научатся, а знающие -

вспомнят ещё раз .

Цель: освоить способы быстрого счета натуральных чисел

Главная задача нашей работы – это создание базы данных, включающей :

• Правила быстрого счета

• Набор практических заданий

• Использование презентаций как учебное пособие

Приемы быстрого счёта

• Умножение на 4, деление на 4
• Умножение 25 на 25, 35 на 35 и т.д.
• Умножение на 11
• Умножение на число 111, 1111 и т.д,
• Умножение на 5; 50; 500; …
• Распределительное свойство умножения относительно сложения
• Умножение на число вида аа
• Умножение на 25,250,2500…
• Возведение в квадрат двухзначных чисел

Чтобы число умножить на 4, его дважды удваивают. Например:

:

135 ∙ 4= (135 ∙ 2) ∙ 2=270 ∙ 2=540

Чтобы число разделить на 4, его дважды делят на 2.

• Например:

124 : 4 = (124 : 2) : 2 = 62 : 2 = 31

Умножение 25 на 25, 35 на 35 и т.д.

При умножении количество десятков первого множителя умножаем на увеличенное на 1 количество десятков второго множителя, а после ставим число 25.

Например:

25*25= 2*(2+1) и 25 т.е.=2*3и 25 =625

65*65= 6*7 и 25 =4225

Умножение на 11

• 1. Умножение на 11 числа, сумма цифр которого не превышает 10.

Чтобы умножить на 11 число, сумма цифр которого 10 или меньше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

• 72 х 11 = 7 (7+2) 2 = 792;
• 35 х 11 = 3 (3+5) 5 = 385;

2. Умножение на 11 числа, сумма цифр которого больше 10.

Чтобы умножить на 11 число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю (третью) цифру оставить без изменения.

78 х 11 = 7 (7+8) 8 = 7(15)8 = 858.

94 х 11 = 9 (9+4) 4 = 9 (13) 4 = 1034;

Умножение на 11

При умножении на одиннадцать, число нужно умножить на 10 и прибавить само себя, то есть то число, которое мы умножаем.

Пример : 110 * 11 = 110 * (10 + 1) = 110 * 10 + 110 * 1 = 1100 + 110 =1210 Ответ: 1210.

Пример: 123 * 11 = 123 * (10 +1) = 123 * 10 + 123 * 1 = 1230 + 123 =1353 Ответ: 1353

Умножение на число 111, 1111 и т.д, зная правила умножения двузначного числа на число 11

Если сумма цифр первого множителя меньше 10, надо мысленно раздвинуть цифры этого числа на 2, 3 и т.д. шага, сложить цифры и записать соответствующее количество раз их сумму между раздвинутыми цифрами. Количество шагов всегда меньше количества единиц на 1.

Пример:

24 х 111 = 2 (2 + 4) (2+4) 4 = 2664

(количество шагов – 2)

24 х 1111 = 2 (2 +4) (2 +4) (2+4) 4 = 26664 (количество шагов – 3)

Умножение двузначного числа на 111, 1111, 1111 и т.д., сумма цифр которого равна 10 или больше 10

Немного сложнее выполнить устное умножение, если сумма цифр первого множителя равна 10 или

более 10.

Примеры:

48 х 111 = 4 (4+8) (4+8) 8 = 4 (12) (12) 8 = (4 +1) (2+1) 28 = 5328.

В этом случае к первой цифре надо прибавить 1. Получим 5.

Далее 2 + 1 = 3. А последние цифры 2 и 8 оставляем без изменения.

• 56 х 11111 = 5(5+6)(5+6)(5+6)(5+6)6 = =5(11)(11)(11)(11)6 = 622216
• 67 х 1111 = 6(6+7)…7 = 6(13)…7 = 74437

0, ax + b     решение данных неравенств можно просмотреть как этап при решении квадратных неравенств        " width="640"

Линейные неравенства

Линейными

называются неравенства вида:

ax + b 0, ax + b

решение данных неравенств можно просмотреть как этап при решении

квадратных неравенств     

КВАДРАТНЫЕ НЕРАВЕНСТВА

• Квадратными (строгими и нестрогими) называются неравенства вида

a( x – x1)( x – x2) в соответствии со знаком произведения (– или + )

выбирается ответ

Пример 1.   Решите неравенство  

Пример 1.   Решите неравенство  

Решение:

Решение:

Найдем корни квадратного трехчлена  

Найдем корни квадратного трехчлена  

. 

Далее имеем рисунок № 4

. 

Далее имеем рисунок № 4

Ответ:  

Ответ:  

стоят знаки " width="640"

Сформулируем правило расстановки знаков при решении неравенств вида

На координатную ось наносят числа x 1 ,x 2 ,...,x n , которые разбивают её на интервалы знакопостоянства функции, стоящей в левой части неравенства. В промежутке справа от x n ставят знак “+”, затем, двигаясь справа налево, при переходе через точку x i меняют знак, т.е. левее x n ставят знак ”–”, затем “+” и т.д.

Множество решений неравенства будет

объединение интервалов,

в каждом из которых поставлен знак “+”.

Аналогично может быть описано решение неравенств, в которых вместо знака стоят знаки

Иррациональные неравенства

Пример №2.

Начнём с того, что определим Область Допустимых Значений (ОДЗ) переменной   x .  Ясно, что наличие квадратного корня в неравенстве даст условие:

9x-20 ≥ 0 ,

x ≥ 20/9

Теперь, решим уравнение:

Корни, которого, равны: 4 и 5. Оба корня попадают в ОДЗ нашего неравенства

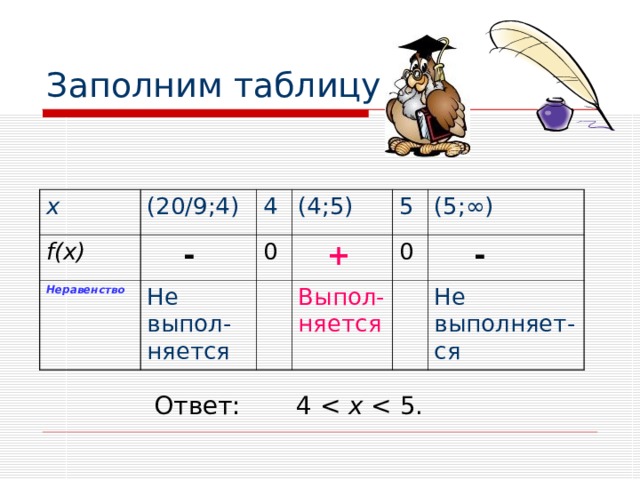
Заполним таблицу

x

(20/9;4)

f(x)

-

4

Неравенство

Не выпол-няется

0

(4;5)

+

5

(5;∞)

Выпол-няется

0

-

Не выполняет-ся

Ответ:       4 x

Простейшие показательные неравенства

.

Пример 3

Решение

Пусть

Тогда после простейших преобразований получаем

Откуда, возвращаясь к переменной x и логарифмируя , имеем:

Ответ:

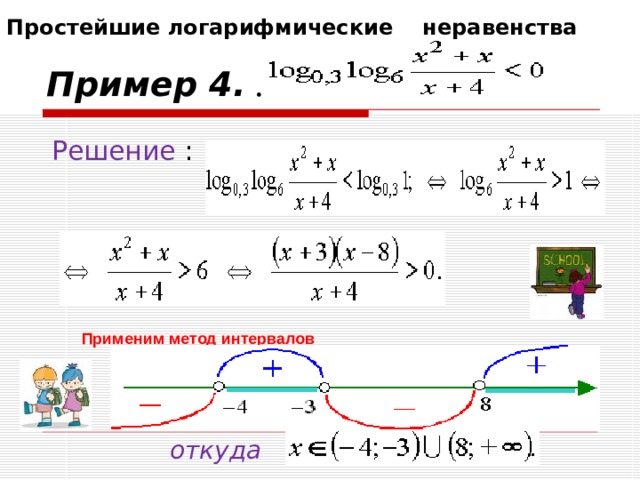
Простейшие логарифмические неравенства

Пример 4. .

.

Решение :

Применим метод интервалов

откуда

Простейшие неравенства с модулем Пример 5

.

Отметим на вещественной оси точки, в которых выраженияпод знаком модуля обращаются в нуль . Таким образом, выделяются интервалы знакопостоянства этих выражений.

Тогда исходное неравенство равносильно совокупности систем:

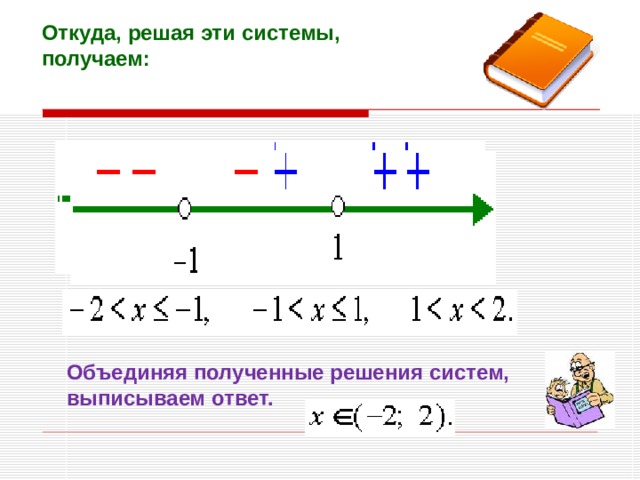
Откуда, решая эти системы, получаем:

Объединяя полученные решения систем, выписываем ответ.

Выводы и предложения:

• Данная модель исследования способна решать обучающие задачи по теме «Метод интервалов»
• Данная тема настолько обширна, что возникает необходимость продолжать работу( например при изучении исследования функций на монотонность и экстремумы)

Выводы и предложения:

• Использовать систематизированный материал как учбное пособие при подготовке к ЕГЭ.
• Предлагаемые домашние задания по пройденным разделам:

Задачи для самостоятельного решения

Решить неравенства

Ответы

ЖЕЛАЕМ УСПЕХА!

Литература

• Агафонов Б.Г.Повторим математику. Издательство «Высшая школа» М.1968 г.
• Агалаков С.А. Математика Е.Г.Э.(часть «С».Омск-2004.
• Дорофеев Г.В. , М.К.Потапов. Пособие по математике «Нестандартные задачи». Издательство «Наука» М.1976 г.
• Далингер В.А. Нестандартные уравнения , неравенства и методы их решения.Омск-1995 г.
• Моденов В. П. Пособие для поступающих в вузы. Издательство «Наука» 1984 г.
• Шарыгин И.Ф. Факультативный курс по математике

М. «Просвещение» 1991 г.