
Samarqand viloyati Kattaqo’rg’on shahar XTB ga qarashli 13-umumiy o’rta ta’lim maktabi matematika fani o’qituvchisi Xudayqulova Naziraning matematika fanidan 3-maktabda
PISA uchun tayyorlagan
TAYANCH DARS ISHLANMASI
„Burchak turlari: to’g’ri, o’tki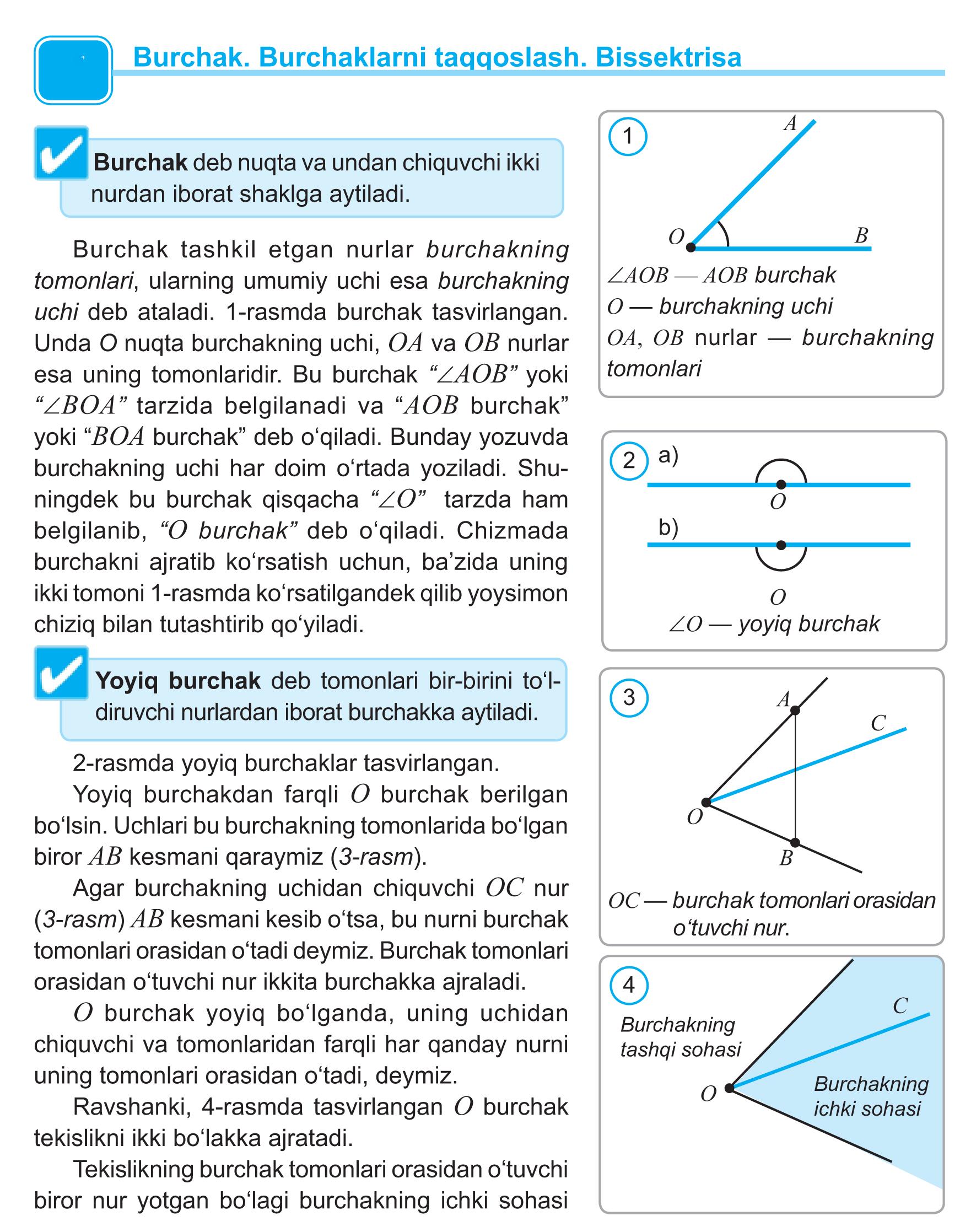
Burchak — bir nuqtadan chiqqan ikki nur (yarim toʻgʻri chiziq)dan tashkil topgan shakl. Nurlar B. tomonlari, ular chiqadigan nuqta B. uchi deb ataladi. Uchidagi harf yordamida B. /LA shaklida, uchi va tomonlarida yotgan nuqtalar yordamida .VAS shaklida belgilanadi. B. tomonlari orqali tekislik oʻtkazilsa, u tekislikni ikki qismga ajratadi. Agar B. tomonlaridan nurlarni B. uchidan qarshi tomonga davom ettirganda u tekislikning qaysi qismini kesmasa, shu qism B.ning ichki tomoni deb ataladi. Tomonlari bir toʻgʻri chiziqni tashkil qilgan B. yoyiq, uning yarmi esa toʻgʻri B. deb ataladi. Toʻgʻri B.dan kichik B.lar oʻtkir. kattalari oʻtmas B. deyiladi. Bir tomoni umumiy, qolgan ikki tomoni bir toʻgʻri chiziqni tashkil qiluvchi B. qoʻshni B.lar, ikki toʻgʻri chiziqning kesishishidan hosil boʻlgan B.lar vertikal B.lar deb ataladi. Tekislikdagi B.ning ichki qismi gradus yoki radian (=57°)larda oʻlchanadi. Maye, yoyiq B. 180° yoki p, toʻgʻri B. 90° yoki p/2 ga teng boʻladi.
B.ni teng ikkiga boʻluvchi nur uning bissektris a s i deyiladi. Ikki toʻgʻri chiziqni uchinchi toʻgʻri chiziq kesib oʻtganda hosil boʻlgan B.lar quyidagicha ataladi (rasm): / bilan 5; 2 bilan b; J6H 7; 4 bilan 8 B.lar moye B.lar; 3 bilan 6; 4 bilan 5 B.lar ichki almashinuvchi; / bilan 8; 2 bilan 7 B.lar tashki almashinuvchi B.lar; 3 bilan 5; 4 bilan 6 B.lar ichki bir tomonli; 1 bilan 7; 2 bilan 8 tashqi bir tomonli B.lar.[1]
Shuningdek tekislikning ushbu nurlar orasidagi barcha nuqtalaridan hosil boʻlgan shaklga ham burchak deyiladi. Umuman aytganda, bu ikki nur ikkita burchak hosil qiladi, chunki ular tekislikni ikkiga boʻladi. Shu burchaklardan biri ichki, boshqasi esa tashqi deyiladi.
Burchak {\displaystyle \angle } belgisi bilan ifodalanadi, bu belgini 1634-yili fransuz matematigi Pierre Hérigone taklif qilgan.
M atematik ifodalarda α, β, γ, θ, φ va hk yunon harflari bilan belgilanadi. Pi bilan adashtirmaslik uchun π belgisi bilan burchak belgilanmaydi.
atematik ifodalarda α, β, γ, θ, φ va hk yunon harflari bilan belgilanadi. Pi bilan adashtirmaslik uchun π belgisi bilan burchak belgilanmaydi.

1. Berilgan qaysi rasmda burchak -1800 ga burilgan?
1)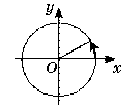 2)
2)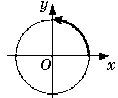 3)
3) 4)
4)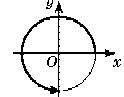 5)
5)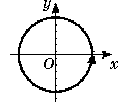 6)
6)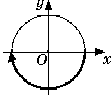
A) 6. B) 2. C) 4 D) 3
2.Berilgan qaysi rasmda burchak 1800 ga burilgan?
1) 2)
2) 3)
3) 4)
4) 5)
5) 6)
6)
A) 3 . B) 2. C) 4 D) 6
3.Berilgan qaysi rasmda burchak 3600 ga burilgan?
1) 2)
2) 3)
3) 4)
4) 5)
5) 6)
6)
A) 4. B) 2. C) 5 D) 3
4.Berilgan qaysi rasmda P(1;0) nuqta (0;-1) ga kelgan ga burilgan?
1) 2)
2) 3)
3) 4)
4) 5)
5) 6)
6)
A) 4 B) 2. C) 3 D) 5
5.Berilgan qaysi rasmda P(1;0) nuqta 300 ga burilgan?
1) 2)
2) 3)
3) 4)
4) 5)
5) 6)
6)
A) 1. B) 2. C) 4 D) 3
TO’G’RI BURCHAK O’TKIR BURCHAK O’TMAS BURCHAK
BURCHAK BISSEKTRISASI O’TMAS BURCHAK

 Получите свидетельство
Получите свидетельство Вход
Вход











 Burchak va uning turlari (3.08 MB)
Burchak va uning turlari (3.08 MB)
 0
0 3715
3715 12
12 Нравится
0
Нравится
0



