Бегущая волна и ее уравнение. Стоячая волна и ее уравнение

Пашикова Т.Д.

Преподователь кафедры общей физики

Туркменский государственный университет им. Махтумкули

(г. Ашхабад, Туркменистан)

Бегущая волна и ее уравнение. Стоячая волна и ее уравнение

Бегущая волна – волна, которая переносит энергию в пространстве.

Рассмотрим плоскую гармоническую волну, распространяющуюся по направлению 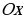. Поверхности волны перпендикулярны 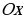, все точки волновой поверхности совершают колебания одинаково, смещение 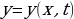. Уравнение колебаний частиц, находящихся на плоскости Х, примет вид:

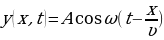(31.1)

Уравнение (31.1) называют уравнением бегущей волны (рис.31.1). Если плоская волна задается при помощи уравнения (31.1), то ее перемещение идет по 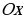. При обратном ее направлении по 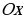уравнение запишется:

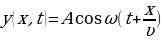(31.2)

Рассмотрим некоторую частицу , находящуюся на расстоянии 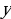от источника колебаний(частицы ). Тогда уравнение колебания частицы следует написать так:

(31.3)

где – время распространения колебаний от до , т.е. время, за которое волна переместилась на 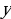. Тогда

(31.4)

Соотношение (31.4), позволяющее определить смещение любой точки волны в любой момент времени, называется уравнением бегущей волны. Подставляя в уравнение (31.4) 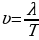и , получим другие формы уравнения волны:

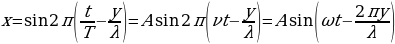(31.5)

Так как прохождение волны сопровождается колебанием частиц среды, то вместе с волной перемещается в пространстве и энергия колебаний.

Важным случаем интерференции волн является сложение двух когерентных волн, движущихся навстречу друг другу вдоль одной прямой. Две бегущие волны, имеющие одинаковые амплитуды, частоты и длины волн и распространяющиеся одновременно в одной и той же среде в противоположных направлениях, при сложении образуют стоячую волну.

Такие волны возникают при сложении падающей волны с волной, отраженной от менее или более плотной среды. Если уравнение первой волны записать в виде

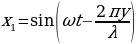
то уравнение второй волны имеет вид

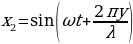
Тогда уравнение результирующей волны представится согласно (29.2) выражением

(31.6)

Уравнение (31.6) показывает, что в точках среды совершаются колебания с частотой 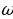и амплитудой , зависящей от координаты 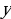этих точек. Причем во всех точках, для которых 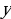удовлетворяет условию

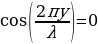, или

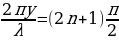(31.7)

амплитуда колебаний равна нулю. Из формулы (31.7) следует, что

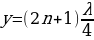
т.е. в точках с координатой 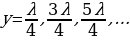колебания всегда отсутствуют. Эти точки называют узлами волны. Точки, расположенные в середине между узлами, колеблются с наибольшей амплитудой, равной 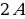. Эти точки называются пучностями волны. Результат наложения двух встречных волн с одинаковыми амплитудами и периодами называется стоячей волной (узлы и пучности все время находятся на одном месте).

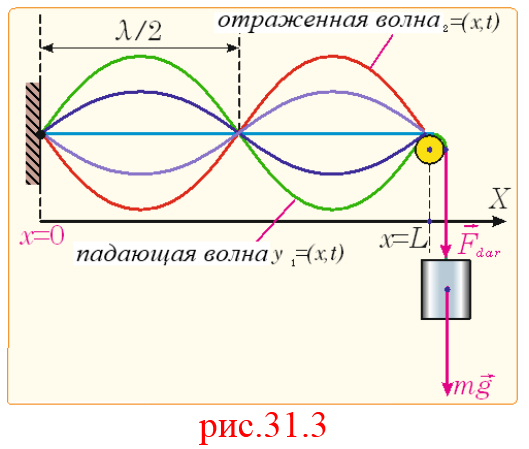На рис.31.3, где изображена часть стоячей волны в моменты времени отчетливо видно,что точки среды,находящиеся в узлах, колебаний не совершают. Точки, расположенные справа и слева от каждого узла, колеблются в противоположных фазах. Расстояние между соседними узлами или пучностями равно половине длины бегущих волн, образующих стоячую волну. Стоячая волна может образовываться только в том случае, если – длина струны кратно целому числу полуволн 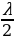(рис.31.3). Этим колебательным модам соответствуют частоты

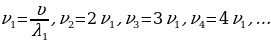(31.8)

Частоты и т.д.являются гармониками основной частоты 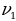рис.31.4.

Будучи неподвижной, стоячая волна не переносит энергии (происходит как бы компенсация переносов энергии двух бегущих в противоположных направлениях волн).

Стоячие волны обычно возникают в ограниченной среде при интерференции бегущей волны и ее отражения от границ среды. Например, волны натянутой струны, воздушного столба в трубе ограниченной длины, водяные волны вблизи вертикальных преград (плотин) и т.п.