Получите свидетельство
Вход
Ф-9 Движение тела под действием нескольких сил
Характерная особенность решения задач механики о движении материальной точки, требующих применения законов Ньютона, состоит в следующем:
Сделать схематический чертёж и указать все силы, действующие на данное тело в текущий момент времени.
Составить основное уравнение динамики в векторной форме F=F1+F2+…+Fn=mа
Найти проекции Fx и Fy составляющих сил по этим осям и затем составить основное уравнение динамики точки в проекции. Положительное направление осей удобно выбирать так, чтобы оно совпадало с направлением ускорения тела.
После того как получена полная система уравнений, можно приступать к ее решению относительно искомого неизвестного.
Выписав числовые значения заданных величин в единицах одной системы, принятой для расчета, и подставив их в окончательную формулу, прежде чем делать арифметический подсчет, нужно проверить правильность решения методом сокращения наименований. В задачах динамики, особенно там, где ответ получается в виде сложной формулы, этого правила в начальной стадии обучения желательно придерживаться всегда, поскольку в этих задачах делают много ошибок.
Чтобы научиться решать задачи по динамике, нужно научиться задавать вопросы и искать на них ответы на всех этапах решения задач.
С каких вопросов начать?
| 1. Где должны располагаться точки, являющиеся началом вектора каждой из сил? | Если тело движется поступательно, то все точки совершают одинаковые перемещения. Размеры тела в этом случае не имеют значения. Поэтому для удобства все силы прикладываем к одной точке, находящейся в центре тяжести. |
| 2. Как учесть все, действительно приложенные, силы и не изобразить лишнюю? | Сила – характеристика действия реального тела. Если не можешь ответить на следующий вопрос: со стороны какого тела приложена сила? – Следовательно силы нет. |
Рассмотрим несколько примерв, в которых необходимо изобразить все приложенные силы.
1. Санки тянут по рыхлому снегу с силой F под углом ά к горизонту. Изобразите все силы, действующие на санки.
| 1. С чего начнём? | В центре прямоугольника ставим точку – это начало всех векторов сил. |
| 2. Как правильно изобразить все силы? | Для каждой силы выясним: со стороны какого объекта приложена сила. |
| Сила | Что(кто) действует? |
|
|
|
|
|
| Fт | Тот кто тянет санки |
|
А теперь самостоятельно изобразите, какие силы действуют:
3. Эти же санки катятся с горы.
4. На нити поднимают тело вертикально вверх.
5. Тело крепится к нити и опускается в жидкость.
Проекция сил в двухмерной системе координат.
| Как спроектировать вектор силы на оси координат? | Из начала и конца вектора опускаем перпендикуляры до пересечения с осью координат |
|
| Как удобнее расположить систему координат? | Поместить начало координат в начало вектора | |
| Как выразить проекцию через модуль вектора силы? | Вектор, его проекция на одну из осей и перпендикуляр образуют прямоугольный треугольник. Для угла ά: Fx=Fcosά Fy=Fsinά |
Найдём проекцию на оси Х и У всех сил, приложенных к телу.
F1x=Fcosά F1y=Fsinά; F2x=-F2 F2у=0; F3х=0 F3у=-F3; F4х=0 F4у=F4
Найдите самостоятельно проекции на оси Х и У всех сил, приложенных к телу.
| 1. Тело соскальзывает с наклонной плоскости. |
| 2. Тело на верёвке. |
|
|
|
|
Решение задач по динамике основано на применении 2-го закона Ньютона.
Задача. Найдите величину ускорения тела, соскальзывающего по наклонной плоскости с нулевой начальной скоростью. Угол наклона плоскости с горизонту 30. Коэффициент трения скольжения тела по плоскости 0,3.
| Дано: |
|
|
Задача. Тележка массой 5 кг движется по горизонтальной поверхности под действием гири массой 2 кг, прикрепленной к концу нерастяжимой нити, перекинутой через неподвижный блок. Определить натяжение нити и ускорение движения тележки, если коэффициент трения тележки о плоскость 0,1. Массами блока и нити, а также трением в блоке пренебречь.
| Дано: | Решение: |
|
| 1. На тележку действуют силы: сила тяжести mg, сила реакции плоскости Т, сила трения Fтр, выберем прямоугольную систему координат хОу, направим ось х по направлению движения тележки, а ось у – вертикально вверх. Запишем второй закон Ньютона в векторной форме. |
| |
| 2. На гирю m2 действуют две силы: сила тяжести m2g и сила натяжения нити Т2. Запишем второй закон Ньютона для второго тела. |
| |
| 3. Сила натяжения и ускорения системы тел равны, следовательно находим силу натяжения и ускорение. |
|
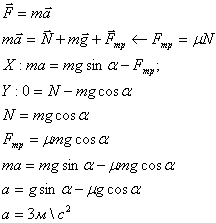
Алгоритм решения задач механики о движении материальной точки, требующих применения законов Ньютона. (41.78 KB)
0
56
1
Нравится
0
