3D построения в Scilab

3D построения

в Scilab

Выполнила

Студентка гр.МДМ-113

Губина Лидия

Scilab – это система компьютерной математики, которая предназначена для выполнения инженерных и научных вычислений, таких как:

• решение нелинейных уравнений и систем;

• решение задач линейной алгебры;

• решение задач оптимизации;

• дифференцирование и интегрирование;

• задачи обработка экспериментальных данных (интерполяция и аппроксимация, метод наименьших квадратов);

• решение обыкновенных дифференциальных уравнений и систем.

Построение трехмерных графиков в Scilab

Процесс построения графика функции вида Z(x, y) можно разделить на три этапа:

1. Создание в области построения графика прямоугольной сетки. Для этого формируются прямые линии, параллельные координатным осям x i и y j .

2. Вычисление значений функции z ij = f(x i , y j ) во всех узлах сетки.

3. Обращение к функции построения трехмерных графиков.

Как изобразить 3D поверхность?

Способ 1. С помощью команды plot3d . Команда создает 3D график по точкам, заданным матрицами x, y и z.

Способ 2. С помощью команды plot3d1 . Команда создает 3D график по точкам, заданным матрицами x, y и z с помощью уровней цвета. Вещь в общем избыточная: величина координаты z дополнительно еще и покрашена, в зависимости от принимаемого значения z.

Способ 3. С помощью команды fplot3d . Это аналог команды fplot3d, но изображаемая поверхность задана с помощью внешней функции.

Способ 4. С помощью команды fplot3d1 . Это аналог команды plot3d1, но изображаемая поверхность задана с помощью внешней функции.

Синтаксис этих команд можно узнать с помощью help.

Обращение к функциям следующее:

plot3d(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen]),

plot3d1(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen]),

здесь x – вектор-столбец значений абсцисс; y – вектор-столбец значений ординат; z – матрица значений функции;

theta, alpha – действительные числа, которые определяют в градусах сферические координаты угла зрения на график или это угол, под которым наблюдатель видит отображаемую поверхность;

leg – подписи координатных осей графика – символы, отделяемые знаком @. Например, ’X@Y@Z’.

flag – массив, состоящий из трех целочисленных параметров: [mode,type,box].

Задача 1. Построить график функции Z = t^2 · tan(t).

Листинг программы:

t=[0:0.3:2*%pi]';

z=t^2*tan(t');

plot3d(t,t,z)

Задача 2. Построить график функции Z = 5y 2 – x 2 .  

Листинг программы:

x=[-2:0.1:2];

y=[-3:0.1:3];

for i=1:length(x)

for j=1:length(y)

z(i,j)=5*y(j)^2-x(i)^2;

end

end

plot3d1(x,y,z,-125,51);

colorbar(-2,2)

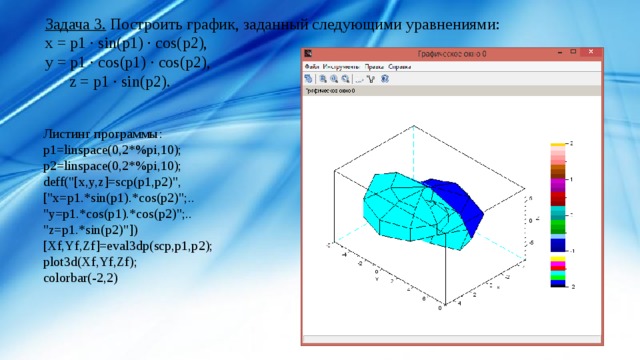
Задача 3. Построить график, заданный следующими уравнениями:

x = p1 · sin(p1) · cos(p2),

y = p1 · cos(p1) · cos(p2),

z = p1 · sin(p2).

Листинг программы:

p1=linspace(0,2*%pi,10);

p2=linspace(0,2*%pi,10);

deff("[x,y,z]=scp(p1,p2)",["x=p1.*sin(p1).*cos(p2)";..

"y=p1.*cos(p1).*cos(p2)";..

"z=p1.*sin(p2)"])

[Xf,Yf,Zf]=eval3dp(scp,p1,p2);

plot3d(Xf,Yf,Zf);

colorbar(-2,2)

Функции plot3d2 и plot3d3 являются аналогами функции plot3d, поэтому имеют такой же синтаксис:

plot3d2(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen]),

plot3d3(x,y,z,[theta,alpha,leg,flag,ebox][keyn=valuen])

Задача 4. Построить сферу при помощи функции plot3d2.

Листинг программы:

u = linspace(-%pi/2,%pi/2,40);

v = linspace(0,2*%pi,20);

X = cos(u) '*cos(v);

Y = cos(u) '*sin(v);

Z = sin(u) '*ones(v);

plot3d2(X,Y,Z);

e=gce();

e.color_mode=3

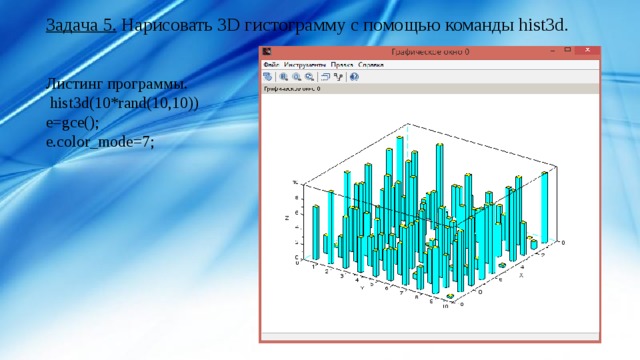
Задача 5. Нарисовать 3D гистограмму c помощью команды hist3d.

Листинг программы.

hist3d(10*rand(10,10))

e=gce();

e.color_mode=7;

Спасибо за внимание