Получите свидетельство
ВходПеревод чисел из десятичной системы счисления в восьмеричную и наоборот.
В этом уроке информатики мы рассмотрим как перевести любое число из десятичной системы счисления в восьмеричную, а затем переведем произвольное число из восьмиричной системы счисления в десятичную, то есть сделаем обратное действие.
Итак в десятичной системе счисления мы пользуемся 10 цифрами с помощью которых можем составить любое число. Это цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В восьмеричной системе счисления у нас только восемь цифр 0, 1, 2, 3, 4, 5, 6, 7, с помощью которых мы можем составлять любые числа.
В восьмеричной системе счисления после семерки идет цифра 10 т.к. цифры 8 в ней нет. Почему? А потому что когда мы работаем в десятичной системе счисления то когда доходим до 9 то при прибавлении к ней единицы 9+1 получаем, что 9 заменяется на ноль, слева от которого добавляется 1 (к старшему разряду).
Таким образом мы можем попробовать составить небольшую таблицу соответствия чисел десятичной и восьмиричной системы счисления.
|
Десятичная |
Восьмеричная |
|
1 |
1 |
|
2 |
2 |
|
3 |
3 |
|
4 |
4 |
|
5 |
5 |
|
6 |
6 |
|
7 |
7 |
|
8 |
10 |
|
9 |
11 |
|
10 |
12 |
|
11 |
13 |
|
12 |
14 |
|
13 |
15 |
|
14 |
16 |
|
15 |
17 |
|
16 |
20 |
|
17 |
21 |
|
18 |
22 |
|
19 |
23 |
|
20 |
24 |
|
21 |
25 |
|
22 |
26 |
|
23 |
27 |
|
24 |
30 |
|
25 |
31 |
|
26 |
32 |
|
27 |
33 |
|
28 |
34 |
|
29 |
35 |
|
30 |
36 |
|
31 |
37 |
То есть, смотрите, когда мы выписывали правый столбец (числа в восьмеричной системе счисления) мы руководствовались тем правилом, которое описали выше таблицы. Как только у нас заканчиваются цифры системы счисления мы пишем ноль и добавляем единицу к старшему разряду.
А теперь рассмотрим как перевети число из десятичной системы счисления в восьмеричную. Давайте возьмем число 259 в десятичной системе счисления.
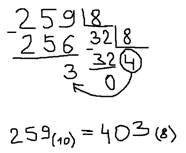
Число в десятичной системе счисления делим на основание степени (восьмерку). Получаем какую то целую часть и остаток. Если целая часть больше либо равна 8, то опять делим на основание степени и получаем целую часть и остаток. Как только целая часть становится меньше восьми, начинаем выписывать, сначала последнюю целую часть, а затем все остатки в обратном порядке. Это и будет число в новой системе счисления, в нашем случае в восьмиричной.
И сделаем обратное преобразование переведем число 403 в восьмеричной системе счисления в десмятичную.
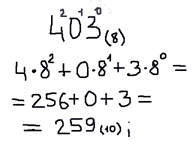
То есть вначале мы нумеруем числа справа налево для того, чтобы затем каждое из чисел в восьмиричной системе счисления умножить на восьмерку в соответствующей степени. Сложив все, мы получим результат в десятичной системе счисления.
Получите комплекты видеоуроков + онлайн версии
Похожие записи
433987
Нравится
0
Заранее спасибо за помощь! :)
как представлено число 75(в десятичной) в восьмеричной системе счисления.
У меня получилось-93, а в ответе должно быть 113.Почему так?((
Извините , просто не досчитала до конца, все получилось))
Да, просто 9 еще нужно было расписать по разрядам восьмеричной системы счисления
как представлено число 75(в десятичной) в восьмеричной системе счисления.
У меня получилось-93, а в ответе должно быть 113.Почему так?((
б)123,4(8) перевести в (16)
В первом примере разбиваете числа на триады и переводите их в 8-ричную сс.
Важно! Целая часть разбивается с права-налево, дробная слева-направо, т.е. все от разелительной точки. Если не хватит цифр для полных троек дописываем незначащие нули.
Второй пример. Переводим в двоичную каждую цифру, разбиваем на тетрады, пописывая при необходимости незначащие нули, как в предыдущем примере и переводим их в 16-тиричную СС.
Решите пожалуйста
1) 356(8-в восмерич.сист.счисл) х 17(8-в восмерич.сист.счисл)
2) 646(8-в восмерич.сист.счисл) х 27(8-в восмерич.сист.счисл)
3) 705(8-в восмерич.сист.счисл) х 13(8-в восмерич.сист.счисл)
4) 1011(2 - в двоичной сист.счисл) / 1100(2-в двоичной сист.счисл)
Ну да тут нужно посидеть посчитать... Числа не маленькие для подобных заданий...
Переведите все в десятичную систему счисления и посчитайте, а потом ответ переведите обратно в нужную вам систему счисления.