Множество действительных чисел

Вопросы занятия:

·  повторить все изученные ранее множества чисел;

·  вспомнить, что множество действительных чисел является объединением множеств рациональных и иррациональных чисел;

·  вспомнить, что множество рациональных чисел включает множество целых чисел и все дроби, кроме бесконечных непериодических.

Материал урока

Сначала вспомним, что понимают под словом множество в математике.

Определение

Множество — это совокупность некоторых объектов, объединённых по какому-либо признаку.

Приведём примеры множеств:

Множество принято обозначать заглавной латинской буквой.

Вы же помните, что множество чисел, которые используются для счёта, называют множеством натуральных чисел и обозначают буквой N.

Самое время, говоря о множестве натуральных чисел, вспомнить понятие числового множества.

Определение.

Числовое множество – множество, элементами которого являются числа.

Элементы множества записывают в фигурных скобках. Так элементами множества натуральных чисел, являются числа 1, 2, 3 и так далее.

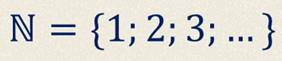
Определение.

Множество А называют подмножеством множества B, если каждый элемент множества А является элементом множества B. Записываю это так.

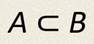
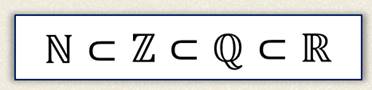
Мы с вами ранее говорили о множестве целых чисел. Оно состоит из натуральных чисел, чисел противоположных натуральным и нуля.

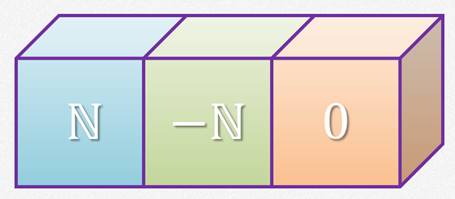
Хорошо видно, что каждый элемент множества натуральных чисел принадлежит множеству целых чисел. То есть множество N является подмножеством множества Z.

Сейчас вернёмся к одному из рассмотренных ранее способов представления обыкновенной дроби в виде десятичной.

Мы с свами при повторении этого вопроса рассматривали 3 примера, в которых получили конечную десятичную дробь и бесконечные периодические десятичные дроби.

Но вам известно ещё и о существовании бесконечных непериодических десятичных дробей.

Это бесконечная десятичная дробь, в которой нет периода. В качестве примера такой дроби можно привести хорошо известное вам число π.

Так множество бесконечных непериодических дробей составляет множество иррациональных чисел.

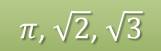
В свою очередь множество рациональных чисел содержит в себе множество целых чисел, конечных десятичных дробей и бесконечных периодических дробей.

Понятно, что любое целое число можно представить в виде обыкновенной дроби со знаменателем 1. Также вы знаете, как любую конечную десятичную дробь и любую бесконечную периодическую десятичную дроби можно представить в виде обыкновенной.

Тогда можно дать такое определение рациональному числу.

Определение.

Рациональное число – число, которое можно представить в виде дроби, где числитель является целым числом, а знаменатель — натуральным.

Рациональные и иррациональные числа в совокупности составляют множество действительных чисел.

Из этих иллюстраций видно, что множество Z целых чисел является подмножеством множества рациональных чисел. А множество рациональных чисел является подмножеством множества действительных чисел.

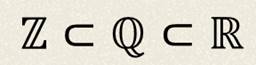
И ранее мы говорили, что множество натуральных чисел является подмножеством множества целых чисел.

Мы говорили, что любую конечную десятичную дробь и любую бесконечную периодическую десятичную дроби всегда можно представить в виде обыкновенной.

С конечной десятичной дробью сложностей не должно возникать, мы на предыдущих уроках рассматривали такие случаи.

А вот правило обращения периодической десятичной дроби в обыкновенную стоит напомним. Рассмотрим его подробнее.

Выполним несколько заданий, где и применим знания о множествах чисел.

Пример

Пример

Пример

Пример

Теперь вернёмся к понятию множества и подробнее поговорим о пересечении и объединении множеств.

Определение.

Объединением (или суммой) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит хотя бы одному из этих множеств.

Определение.

Пересечением (или произведением) множеств А и В называется множество, состоящее из элементов, каждый из которых принадлежит и множеству А, и множеству В одновременно.

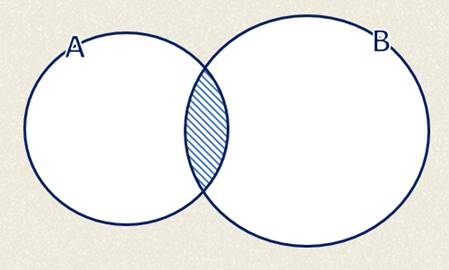
Пользуясь этими определениями найдём объединение и пересечение множеств натуральных и целых чисел.

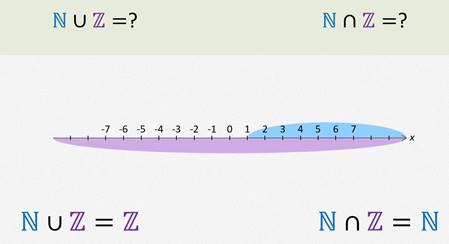
Итак, пересечением данных множеств является множество натуральных чисел, а объединением — множество целых чисел.

Итоги урока

Мы с вами повторили все изученные ранее множества чисел. Множество действительных чисел является объединением множеств рациональных и иррациональных чисел.

Множество рациональных чисел в свою очередь включает множество целых чисел и все дроби, кроме бесконечных непериодических, которые и составляют множество иррациональных чисел.

Ну, а в множество целых чисел входят натуральные, противоположные натуральным и 0.

И справедлива такая запись, которая демонстрирует связь всех известных нам числовых множеств.