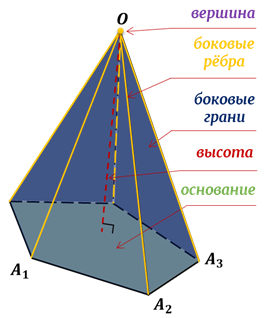
Напомним,
что пирамида – это многогранник, в основании которого лежит 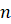 –угольник,
а остальные
–угольник,
а остальные 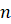 граней
– треугольники с общей вершиной.
граней
– треугольники с общей вершиной.
Многоугольник
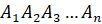 называется
основанием пирамиды.
называется
основанием пирамиды.
Треугольники
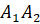 ,
,
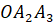 ,
…,
,
…, 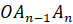 называются
боковыми гранями пирамиды.
называются
боковыми гранями пирамиды.
Точка
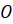 –
вершиной пирамиды, а отрезки
–
вершиной пирамиды, а отрезки 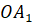 ,
,
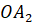 ,
…,
,
…, 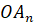 –
её боковыми рёбрами.
–
её боковыми рёбрами.
Отрезок, соединяющий вершину пирамиды с плоскостью её основания и перпендикулярный к этой плоскости, называется высотой пирамиды.
Пирамиду
с вершиной 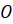 и
основанием
и
основанием 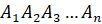 называют
называют
 -угольной
пирамидой и обозначают так:
-угольной
пирамидой и обозначают так:  .
.
Диагональное сечение – это сечение пирамиды плоскостью, которая проходит через два боковых ребра, не принадлежащих одной грани.

Объединение боковых граней называется боковой поверхностью пирамиды, а объединение всех граней называется полной поверхностью пирамиды.
Тогда площадью боковой поверхности пирамиды называется сумма площадей её боковых граней.
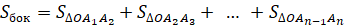
А площадью полной поверхности пирамиды называется сумма площадей всех её граней.
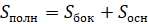
Объём пирамиды равен:
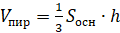 .
.
Пирамида, в зависимости от того, какой многоугольник лежит в основании, имеет своё название.
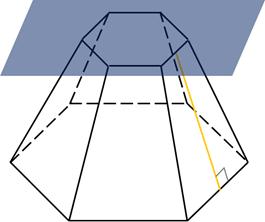
Пирамида называется правильной, если её основанием является правильный многоугольник, а все боковые рёбра равны.
Отрезок, соединяющий вершину пирамиды с центром основания, является её высотой.
Высота боковой грани правильной пирамиды, проведённая из её вершины к ребру основания, называется апофемой.
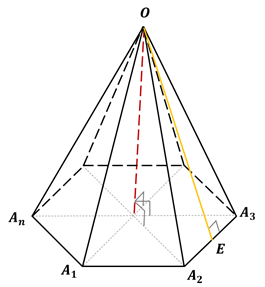
Выше
изображена правильная пирамида. 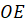 –
одна из её апофем. Все апофемы правильной пирамиды равны друг другу.
–
одна из её апофем. Все апофемы правильной пирамиды равны друг другу.
Отметим
некоторые свойства правильной 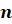 -угольной
пирамиды.
-угольной
пирамиды.
1.
В правильной 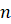 -угольной
пирамиде все боковые рёбра равны между собой.
-угольной
пирамиде все боковые рёбра равны между собой.
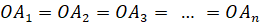
2. Боковые рёбра равно наклонены к основанию.
3. Из равенства боковых рёбер пирамиды следует и равенство её боковых граней.
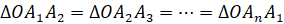
4. Боковые грани равно наклонены к основанию.
5. Вершина проектируется в центр основания (основание высоты совпадает с центром основания).
6. Площадь боковой поверхности правильной пирамиды равна:
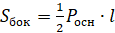 .
.
7.
Объём правильной четырёхугольной пирамиды со стороной основания 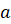 и
высотой
и
высотой 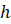 равен:
равен:
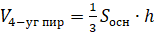 .
.
Параллельное сечение пирамиды – сечение пирамиды плоскостью, параллельной основанию.
Параллельное сечение пирамиды обладает следующими свойствами:
1. сечение, параллельное основанию пирамиды, отсекает на высоте пирамиды и боковых рёбрах пропорциональные отрезки;
2. в сечении получается многоугольник, подобный основанию;
3. площади сечения и основания относятся как квадраты их расстояний до вершины.

Усечённая пирамида – это часть пирамиды, заключённая между основанием и параллельным сечением пирамиды.
Основания усечённой пирамиды – подобные многоугольники, лежащие в параллельных плоскостях.
Боковые грани усечённой пирамиды – трапеции.
Высота усечённой пирамиды – это перпендикуляр, опущенный из любой точки верхнего основания на плоскость нижнего.
Площадь полной поверхности усечённой пирамиды равна сумме площади боковой поверхности и площадей двух оснований.
Объём усечённой пирамиды равен разности объёмов полной и отсечённой пирамиды, или его ещё можно вычислить по следующей формуле:
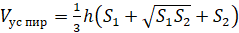 .
.
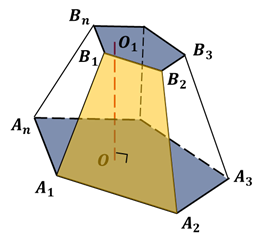
Правильная усечённая пирамида получается из правильной пирамиды.
Апофема – высота боковой грани правильной усечённой пирамиды.
Площадь боковой поверхности правильной усечённой пирамиды равна:
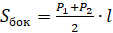 .
.
Основные моменты мы с вами повторили, а теперь давайте перейдём к практической части занятия.
Задача
первая. Дана треугольная пирамида, боковые рёбра которой
взаимно перпендикулярны и равны 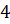 см,
см,
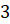 см
и
см
и 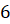 см.
Найдите площадь боковой поверхности пирамиды.
см.
Найдите площадь боковой поверхности пирамиды.
Решение.

Задача
вторая. Дана правильная четырёхугольная пирамида со стороной
основания 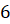 см
и высотой
см
и высотой 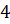 см.
Найдите площадь полной поверхности пирамиды.
см.
Найдите площадь полной поверхности пирамиды.
Решение.


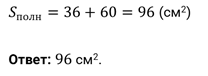
Задача
третья. Найдите высоту правильной усечённой треугольной
пирамиды 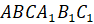 ,
если стороны её оснований равны
,
если стороны её оснований равны 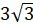 см
и
см
и 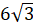 см,
а боковое ребро равно
см,
а боковое ребро равно 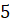 см.
см.
Решение.


Задача
четвёртая. В пирамиде 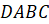 боковое
ребро
боковое
ребро 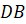 перпендикулярно
основанию и равно ребру
перпендикулярно
основанию и равно ребру 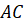 .
Треугольник
.
Треугольник 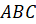 –
прямоугольный с катетами
–
прямоугольный с катетами 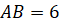 см
и
см
и 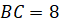 см.
Найдите объём пирамиды.
см.
Найдите объём пирамиды.
Решение.
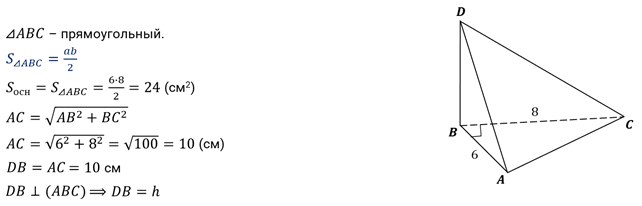
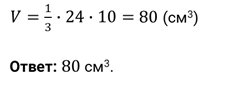
Задача
пятая. Найдите объём правильной треугольной пирамиды с
ребром основания, равным 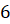 см,
и боковым ребром, равным
см,
и боковым ребром, равным 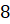 см.
см.
Решение.





 Получите свидетельство
Получите свидетельство Вход
Вход





 12038
12038

