События

Сегодня на уроке мы напомним, чем занимается раздел математики, называемый теорией вероятностей. Назовём важнейшие понятия теории вероятностей. Узнаем, какие события называют случайными, достоверными и невозможными. Выясним, какие события называют элементарными. Поговорим о равновозможных событиях.

Из предыдущих классов вы уже имеете представление о теории вероятностей, теперь мы немного расширим и углубим их.

Итак, в первую очередь отметим, что важнейшими понятиями теории вероятностей являются вероятностный эксперимент (испытание, наблюдение), событие (следствие испытания) и вероятность события.

Вообще, событиями или явлениями называют всё, что происходит или не происходит в реальной действительности. Практикой установлено, что в часто происходящих случайных событиях существуют определённые закономерности. Раздел математики, который занимается исследованием этих закономерностей, называется теорией вероятностей.

Задача теории вероятностей – установление и математическое исследование закономерностей массовых случайных явлений.

Далее поговорим о событиях. Сформулируем определение. Событие называют случайным по отношению к некоторому испытанию (опыту), если в ходе этого испытания оно может произойти, а может и не произойти.

Например, при одном бросании игрального кубика испытание состоит в наблюдении выпавших очков. При проведении испытания возможны следующие события (исходы испытания): на верхней грани кубика может оказаться одно из чисел: 1, 2, 3, 4, 5, 6. Каждое из этих событий является случайным, так как оно может произойти, а может и не произойти.

Следующий пример. Пусть в урне находятся шары белого, красного и чёрного цвета, а испытание заключается в извлечении шара из урны. В результате однократного извлечения шара возможный три события (исхода испытания): «извлечён белый шар», «извлечён красный шар», «извлечён чёрный шар». Каждое из этих трёх событий является случайным, так как оно может произойти, а может и не произойти.

И ещё один пример. При однократном подбрасывании монеты возможны два исхода: выпадение орла и выпадение решки. Каждое из этих событий является случайным, так как оно может произойти, а может и не произойти.

Случайные события обычно обозначаются большими латинскими буквами 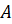, , 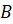 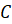и т. д.

Событие 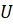 называют достоверным по отношению к некоторому испытанию, если в ходе этого испытания событие 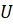 обязательно произойдёт.

Так, например, при одном бросании игрального кубика появление одного из шести чисел 1, 2, 3, 4, 5, 6 будет достоверным событием, так как при бросании кубика оно обязательно произойдёт.

Если испытание заключается в извлечении одного шара из коробки, в которой лежат только красные шары, то извлечение красного шара будет достоверным событием.

Событи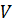е  называют невозможным по отношению к некоторому испытанию, если в ходе этого испытания событие 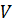 заведомо невозможно.

Пусть, например, в коробке находятся только красные шары, а испытание заключается в извлечении шара из коробки. Тогда событие «извлечён черный шар» является невозможным.

При бросании обычного игрального кубика выпадение числа 7 является невозможным событием.

Предположим, что в результате некоторого испытания обязательно происходит одно из событий и никакие два события не могут произойти одновременно, причём каждое из них не разделяется на более простые. Такие события называют элементарными событиями (или элементарными исходными испытаниями).

Приведём примеры элементарных событий. В испытании с бросанием игрального кубика существует 6 элементарных исходов: выпадение числа 1, выпадение числа 2, выпадение числа 3, выпадение числа 4, выпадение числа 5, выпадение числа 6.

При бросании монеты существует 2 элементарных события: выпадение орла и выпадение решки.

При извлечении одного шара из коробки, в которой находятся один белый шар, один красный шар и один чёрный шар, существует 3 элементарных исхода: извлечение белого шара, извлечение красного шара и извлечение чёрного шара.

Отметим, что рассмотренные в каждом из примеров события несовместны, то есть появление одного из событий исключает появление другого, и единственно возможны, то есть обязательно произойдёт одно из событий. Также в каждом из рассмотренных трёх примеров элементарные события являются равновозможными, то есть у каждого из событий шансы появиться одинаковы.

Кроме элементарных событий, в теории вероятностей рассматриваются и более сложные события. Например, при бросании игрального кубика может быть рассмотрено событие А – появление нечётного числа. Это событие «распадается» на три элементарных события: появление числа 1, появление числа 3 и появление числа 5.

А теперь давайте выполним несколько заданий.

Задание первое. Каким событием (достоверным, невозможным или случайным) является каждое из событий:

1) при комнатной температуре и нормальном атмосферном давлении сталь находится в жидком состоянии;

2) наугад вынутая из кошелька монета оказалась пятирублёвой;

3) наугад названное натуральное число больше нуля;

4) вынутый наугад цветок из букета ромашек оказался розой;

5) в результате броска игрального кубика появилось число ?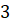

Решение.

Задание второе. Перечислите все элементарные события, которые могут произойти в результате следующих испытаний:

1) на поверхность стола бросается игральный тетраэдр, грани которого пронумерованы числами 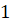, , 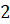, , 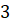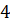и определяется число на той грани, которая лежит на поверхности стола;

2) из коробки, в которой лежат семь шаров семи различных цветов, извлекается один шар и называется его цвет.

Решение.

Задание третье. Выяснить, являются ли события 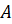 и 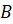 несовместными:

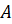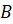1)  – появление туза,  – появление дамы при взятии одной карты из колоды карт;

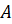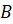2)  – появление туза,  – появление карты пиковой масти при взятии одной карты из колоды карт;

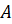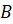3)  – выпадение четырёх очков,  – выпадение чётного числа очков при одном бросании игральной кости;

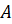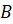4)  – выпадение четырёх очков,  – выпадение нечётного числа очков при одном подбрасывании игральной кости.

Решение.