Логические величины, операции и выражения

На этом уроке мы с вами вспомним, что такое логические величины, проанализируем такие логические операции, как конъюнкция, дизъюнкция и инверсия. Также поработаем с логическими выражениями.

В курсе информатики вы уже проходили логические величины, выражения и операции. Давайте вспомним, что такое высказывание. Высказывание – это повествовательное предложение на любом языке, в котором что-либо утверждается или отрицается. То есть любое высказывание можно определить, как истинное или ложное.

Рассмотрим следующие предложения:

·        Клавиатура предназначена для ввода текстовой информации и команд управления компьютером.

·        При приёме информации происходит процесс переноса информации от источника к приёмнику.

Эти предложения будут относится к высказываниям, так как можно точно сказать истины они или ложны. Первое высказывание является истинным, а второе – ложным.

А вот следующие предложения:

·        Который час?

·        Не поднимай телефон!

Не являются высказываниями, так как в определении сказано, что высказывание – это повествовательно предложение.

Для построения высказываний могут использоваться знаки различных формальных языков: математики, физики, химии и других.

Числовые выражения не являются высказываниями. Но, в то же время, если из двух выражений составить одно и соединить их знаком равенства или неравенства, то новое выражение будет высказыванием.

Логические высказывания бывают простыми и составными.

Простое высказывание – это высказывание, в котором никакая его часть сама не является высказыванием.

Сложное или же составное высказывание – это высказывание, которое строится из простых с помощью логических операций.

Логические величины – это понятия, выражаемые словами Истина (True), Ложь (False). Истинность высказывания выражается через логические величины.

Логическая переменная – это символически обозначенная логическая величина. То есть логическая величина может обозначаться, например, буквой латинского алфавита. Сама же буква будет являться переменной логической величины. В свою очередь, она может принимать только значение Истина или Ложь.

Логическое выражение – это простое или сложное высказывание. Сложное высказывание, как мы уже знаем, строиться из простых при помощи логических операций (связок).

К логическим операциям относятся конъюнкция, дизъюнкция и инверсия (отрицание). Давайте рассмотрим каждую логическую операцию.

Итак, первая логическая операция – конъюнкция – логическое умножение.

Конъюнкция – это логическая операция, которая объединяет два высказывания в одно новое, которое будет являться ложным тогда, когда хотя бы одно из исходных высказываний ложно. Конъюнкция – это двухместная операция, то есть в ней должны присутствовать две логические переменные.

В естественном языке конъюнкция соответствует союзу «И». В алгебре конъюнкция может обозначаться с помощью нескольких знаков: знака амперсанда «&», знака конъюнкции «/\», а также знака умножения «·». В языках программирования для обозначения конъюнкции используется английский союз «AND», знак амперсанда «&» или же двойной знак амперсанда «&&».

Следующая операция – дизъюнкция. Ещё её называют логическим сложением.

Дизъюнкция – это логическая операция, которая объединяет два высказывания в одно новое, которое будет истинным тогда, когда хотя бы одно исходное высказывание истинно. Дизъюнкция также является двухместной операцией, то есть в ней должны присутствовать две логические переменные.

В различных сферах применения, дизъюнкция обозначается по-разному. В естественном языке это союз «ИЛИ». В алгебре высказываний используется следующий знак: «V». Или знак «+». В программировании в основном используется английское «OR». Но в некоторых языках программирования дизъюнкция обозначается следующими знаками: «|», «||».

И последняя логическая операция – инверсия – отрицание.

Отрицание – это логическая операция, которая преобразует исходное высказывание в новое, значение которого противоположно исходному. А вот отрицание является унарной (одноместной) операцией.

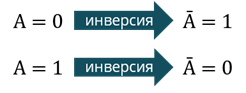
Давайте посмотрим, как обозначается инверсия в различных сферах её применения. В естественном языке инверсии соответствуют речевой оборот «неверно, что» и частица «не». В алгебре высказывания инверсия обозначается следующими знаками: «¬», «ˉ». А вот в сфере программирования используется английское слово «NOT».

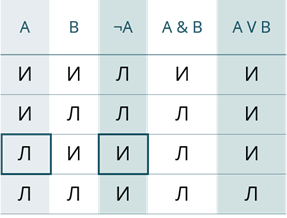
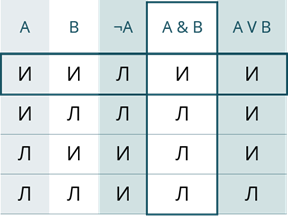
Давайте составим таблицу истинности для всех логических операций. В ней И – это истина, Л – Ложь.

В первых двух столбцах предоставлены всевозможные исходные данные А и B.

В третьем столбце будет идти ¬А.

Как мы с вами знаем из определения операция отрицания преобразует исходное выражение в новое, значение которого противоположно исходному. То есть, если А было истинно, при отрицании оно станет ложным. И наоборот, если выражение было ложным, то оно станет истинным. Заполним третий столбец таблицы исходя из данных первого.

Далее идёт конъюнкция. Здесь мы будем смотреть на значения, которые принимают выражения А и B. Мы с вами знаем, что при конъюнкции новое высказывание будет являться ложным тогда, когда хотя бы одно из исходных высказываний ложно. То есть, исходя из данных нашей таблицы, в первой строке оба высказывания истины, значит и новое будет истинно. А вот все остальные будут ложными, так как во второй строке ложно высказывание B, в третьей – А, а в четвёртой – оба.

И последний, пятый столбец – дизъюнкция. Снова будем брать значения выражений А и B. Новое высказывание будет истинным тогда, когда хотя бы одно исходное высказывание истинно. Значит в первых трёх строках 5 столбца новые выражения будут истинны, так как в первой строке истинны оба высказывания А и B, во второй – А, в третьей – B. А вот в четвёртой строке мы можем видеть, что значения А и B оба ложны, значит и новое выражение будет ложно.

Логическая формула – это формула, которая содержит только логические величины и знаки логических операций. Результатом вычисления такой формулы будет являться истина или ложь.

При выполнении операций в формуле нужно придерживаться следующего порядка:

1)    отрицание;

2)    конъюнкция;

3)    дизъюнкция.

Но также стоит помнить, что операции в скобках выполняются в первую очередь. Если же у нас идут несколько равнозначных операций подряд, то выполнение их будет происходить слева направо.

Давайте разберёмся на примере. Вычислить значение логической формулы, если логические переменные имеют следующие значения: А – Истина, B – истина, C – Ложь.

A & (B V ¬C) V B

Перейдём к решению. Для начала проставим над каждой операцией номер порядка, в котором она будет исполняться.

В первую очередь будут выполняться операции в скобках. А первой будет ¬C.

Затем дизъюнкция: B V ¬C.

После этого будем выполнять конъюнкцию: A & (B V ¬C).

А затем оставшуюся дизъюнкцию: A & (B V ¬C) V B.

Давайте запишем наши вычисления пошагово:

Первое действие – отрицание. Переменная С имеет значение Ложь. Смотрим на таблицу истинности и видим, что при отрицании мы получим значение Истина.

Вторым действием выполняется дизъюнкция. B = Истине, ¬C = Истине. При дизъюнкции двух истин мы получим истину.

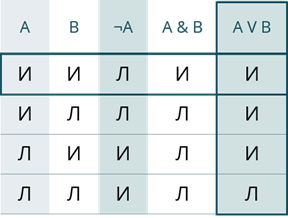
Третье действие. Конъюнкция. А = Истине, B V ¬C = Истине. При конъюнкции двух истин мы получим истину.

И четвёртое действие – дизъюнкция. При дизъюнкции двух истин снова получим истину.

Таким образом значение логической формулы равно истине.

A & (B V ¬C) V B = ИСТИНА

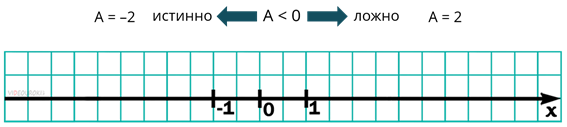
А сейчас рассмотрим логические функции на области числовых значений. Изучением числовых значение занимается алгебра чисел, а логических функций – алгебра логики. Две этих науки могут пересекаться в том случае, если необходимо проверить принадлежность значений алгебраических выражений некоторому множеству. Если нам нужно, например, проверить принадлежность значения числовой переменной А к множеству отрицательных чисел, то это можно выразить через высказывание: «А меньше нуля». В алгебре это можно записать следующим образом: A < 0.

Такое выражение называется в алгебре неравенством. А вот в логике – отношением.

Отношение A < 0 может быть как истинным, так и ложным. Если А – отрицательная величина, то отношение будет истинным, если же А – положительная число или же равно 0, то оно – ложно.

Общий вид структуры отношения такой:

<выражение 1> <знак отношения> <выражение 2>

Выражения 1 и 2 – это некоторые математические выражения, которые принимаю числовые значения. В частном случае выражение может представлять собой одну константу или одну переменную величину. В отношениях могут использоваться следующие знаки: =, <>, >, <, >=, <=.

Из вышесказанного можно сделать вывод, что отношение – это простое высказывание, а значит, логическая величина. Отношение может быть, как постоянным, например, –2<–1 – всегда Истина, 2·2 = 5 – всегда ложно; так и переменной: x > y, a² + b² = c².

Если в отношение входят переменные числовые величины, то и значение отношения будет логической переменной.

Идём дальше. Отношение также можно рассматривать как логическую функцию от числовых аргументов. Например, F (x) = x < 5.

Аргументы определены на бесконечном множестве действительных чисел, а значения функции – на множестве, состоящем из двух логических величин: Истина, Ложь. То есть аргумент может принимать любое числовое значение, а функция только одно из двух: либо Истина, либо Ложь.

Логические функции также называют термином предикат. В алгоритмах предикаты играют роль условий, по которым строятся ветвления и циклы. Предикаты могут быть как простыми логическими функциями, не содержащими логических операций, так и сложными, содержащими логические операции.

Рассмотрим пример. Записать предикат (логическую функцию), который будет принимать значение Истина, если точка на координатной плоскости с координатами (x,y) лежит внутри фигуры, ограниченной линиями. Рисунок предоставлен.

Перейдём к решению. Наша фигура имеет 4 границы, которые можно описать с помощью следующих неравенств:

y > –2;

y < 2;

x > –2;

x < 2;

Из этих четырёх неравенств можно составить систему.

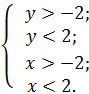
Наш предикат будет равен Истине, если точка с координатами (x, y) будет находится внутри фигуры, то есть будут удовлетворяться все четыре неравенства системы.

Таким образом все четыре отношения должны быть одновременно истинными. Поэтому искомый результат будет выглядеть следующим образом:

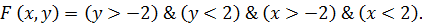
А сейчас давайте рассмотрим логические выражения в языке Pascal.

Как мы с вами уже знаем, в языке Pascal имеется логический тип данных. К логическим константам относятся True (истина) и False (ложь). Все логические переменные будут описываться при помощи типа boolean. Операции отношения осуществляют сравнение двух операндов и определяют, истинно или ложно соответствующее отношение между ними.

Давайте ещё раз вспомним, какие знаки используются в отношениях: равно, не равно, больше, меньше, больше либо равно, меньше либо равно. В языке программирования они будут выглядеть следующим образом:

Также в программировании логические операции записываются не так, как в алгебре логики. Отрицание – not, конъюнкция (логическое умножение) – and, дизъюнкция (логическое сложение) – or. И ещё одна логическая операция – исключающее ИЛИ – xor.

Давайте рассмотрим таблицу истинности для этих операций, а также заполним столбец для исключающего ИЛИ. В таблице латинская буква T обозначает True, а F – False.

Итак, чтобы заполнить столбец для исключающего ИЛИ, будем брать данные из первого и второго столбцов.

Исключающее ИЛИ – это логическая операция, которая объединяет два высказывания в одно новое, которое будет истинным тогда и только тогда, когда одно из исходных высказываний истинно, а второе – ложно. Исходя из этого мы можем сделать вывод, что во второй и третьей строках значение нового высказывания будет равно истине, так как во второй строке высказывание А – истинно, B – ложно. В третьей строке наоборот, А – ложно, B – истинно. В первой и четвёртой строках будет значение – ложь.

Логическое выражение может состоять из логических констант и переменных, отношений, логических операций. Также оно будет принимать одно из двух значение: True или False.

Давайте запишем выражение на языке Pascal. А начнём с примера, который разбирали выше.

A & (B V ¬C) V B

Он будет выглядеть следующим образом:

A and (B or (not C)) or B

В этом примере переменные А, B и C являются переменными типа boolean.

Логические операции выполняются в следующем порядке:

1)    not;

2)    and;

3)    or/xor.

Если же нам нужно, чтобы в первую очередь выполнилась операция, которая имеет более низкий приоритет, необходимо заключать её в скобки. Операции отношения имеют самый низкий приоритет, поэтому если операндами логической операции являются отношения, то их нужно заключать в круглые скобки. Например, математическое неравенство:

5 < A ≤ 42.

На языке Pascal будет записано так:

(A > 5) and (A <= 42).

Также есть такая логическая функция, как odd (A). Она принимает значение True, если значение целочисленного аргумента А является нечётным, и значение False, если значение аргумента А чётное.

При записи сложного логического выражения (предиката) нужно учитывать приоритеты арифметических, логических операций и операций отношений.

1.     Арифметические операции:

1)    – (минус унарный);

2)    *, /;

3)    +, –.

2.     Логические операции:

1)    not;

2)    and;

3)    or, xor.

3.     Операции отношения: =, <>, >, <, >=, <=.

Вспомним предикат, который мы составляли с вами чуть выше. Он выглядит следующим образом:

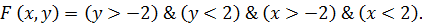
В нём операции отношений заключены в скобки, так как они младше логических операций, но выполняться должны раньше.

Подведём итоги урока.

Сегодня мы с вами вспомнили, что такое высказывание (суждение), логическая величина, логическое выражение, а также какие бывают основные логические операции.

Также мы узнали, что логические выражения в языке Pascal могут принимать одно из двух значений: True – истина или False – Ложь.

Изучили логические операции в языке Pascal, а также расставили приоритеты выполнения действий в логическом выражении на языке Pascal.