Вопросы:
· Разветвляющиеся алгоритмы.
· Логический тип данных.
· Инструкция ветвления.
Линейный алгоритм представляет собой простую и предсказуемую последовательность действий, которые не зависят ни от каких факторов. Однако в повседневной жизни мы не всегда можем однозначно предсказать последовательность действий чего-либо, потому как они зависят от некоторых условий. Например, вы решили пойти на улицу и думаете, что надеть. Ваш выбор одежды будет зависеть от того, какая погода на улице. Можно привести и массу других примеров.
Когда выполняемые действия зависят от некоторых условий, для их записи используются разветвляющиеся алгоритмы. Разветвляющимися называются алгоритмы, содержащие ветвления. Что же такое ветвление? Ветвление – это алгоритмическая конструкция, в которой, в зависимости от некоторого условия, происходит исполнение одной из двух последовательностей действий, которые называются ветвями. Рассмотрим блок-схему ветвления. В верхнем блоке записывается условие. Если условие выполняется, то выполняется одна последовательность команд, в противном случае – другая.
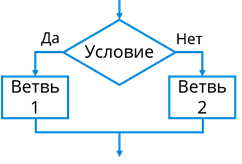
Рассмотрим условие ветвления. В качестве условий в ветвлениях используются логические высказывания. Логическим высказыванием называется утверждение, которое однозначно можно определить как истинное или ложное. Рассмотрим пример. Утверждения о том, что снег белый, в Африке всегда холодно, а человек – хищник, являются логическими высказываниями, так как их правдивость можно легко проверить. А вот вопрос о том, какая сейчас погода, или предложение проверить, не идёт ли на улице дождь, не являются логическими высказываниями, так как вопросы и предложения не являются утверждениями.
Информация об истинности логических высказываний может храниться в логических переменных. Очевидно, что такие переменные могут принимать одно из двух значений: «Истина» или «Ложь». Эти значения могут быть заменены символами двоичного алфавита. Как правило, «Истина» заменяется единицей, а «Ложь» - нулём. Поэтому считается, что «Истина» всегда больше, чем «Ложь». В языке Python логические переменные принадлежат к логическому типу данных, который называется bool — в честь основоположника алгебры и логики Джорджа Буля. Логические переменные в языке Python также могут иметь всего два значения: True, что в переводе на русский язык означает «истина» и False, что означает «ложь». При программировании переменной логического типа можно присвоить один из двух указанных литералов либо результат истинности логического высказывания.
Логическим утверждением в программировании чаще всего является результат одной из операций сравнения. Приведём пример. Утверждение «3 > 2» однозначно истинно, в отличие от «6 = 7». Всего есть шесть операций сравнения: больше, меньше, равно, не равно, больше либо равно и меньше либо равно. В языке Python они записываются знаками >, <, ==, !=, >=, <= соответственно. Все операции сравнения бинарные, то есть могут сравнивать между собой лишь два операнда. Они работают таким образом: сначала вычисляются значения обоих операндов, после чего определяется истинность записанного логического высказывания. Таким образом, операции сравнения имеют самый низкий приоритет из всех.
В интерактивном режиме среды разработки языка Python создадим несколько логических переменных и проверим работу некоторых операций сравнения. Сначала создадим логическую переменную a и присвоим ей значение True. Логические литералы в языке Python всегда записываются с большой буквы. Подтвердим принадлежность переменной a к типу bool, вызвав функцию type (a). Переменная a действительно принадлежит типу bool. Создадим логическую переменную b и присвоим ей результат истинности логического высказывания «3 + 5 < 8». Очевидно, что после этого присваивания переменная b будет иметь значение False, так как 3 + 5 = 8. Теперь запишем логическое высказывание «a > b». Как видим, результатом этого логического выражения является True, так как переменная a имеет значение True, а b - False. При этом всегда True > False.
Логические значения «истина» и «ложь» могут быть неявно преобразованы к числовым значениям единица и ноль соответственно. В доказательство запишем выражение «False + 3». Как видим, результат этого выражения – 3. Запишем выражение: «True + 2». Результат этого выражения – 3.
При использовании операций сравнения важно помнить о соответствии типов операндов. Так можно сравнить между собой две символьные строки или два числа, но при попытке сравнить между собой символьную строку и число программа вернёт сообщение об ошибке. Однако, так как логические выражения могут быть неявно преобразованы к числовым, то их можно сравнивать с числами.
Решим задачу. Написать модуль для определения истинности утверждения о том, что введённое число является положительным.
Начнём написание модуля. Сначала с помощью инструкции print выведем на экран сообщение о том, что это программа, определяющая истинность утверждения о том, что введённое число –положительное и запрос на ввод числа. Дальше считаем число, введённое пользователем в переменную a. Так как в условии задачи не сказано, что число целое, то при считывании будем преобразовывать значение в вещественный тип float. Дальше с помощью инструкции print выведем на экран истинность утверждения «a > 0».
print ('Программа, определяющая истинность утверждения о том, что введённое число - положительное. Введите число.')
a = float (input ())
print (a > 0)
Сохраним написанный модуль и запустим его на выполнение. Введём число 3. Это число положительное, поэтому программа вывела значение True, то есть «Истина». Снова запустим модуль на выполнение и введём число -1. Программа вывела значение False, так как введённое число отрицательное. Программа работает правильно. Задача решена.
Рассмотрим алгоритмы, в которых последовательность действий изменяется в зависимости от входных данных. Для записи таких алгоритмов в языке Python используется инструкция ветвления. Эта инструкция является составной, то есть она содержит в себе другие инструкции. Рассмотрим её запись. Она начинается со служебного слова if, после которого, через пробел, следует условие ветвления. Условием ветвления является выражение логического типа. Дальше следует двоеточие, после которого, начиная со следующей строки с отступом, записываются инструкции, которые будут выполняться в том случае, если условие ветвления будет возвращать значение «истина». Далее на одном уровне со словом if следует служебное слово else, после которого записывается двоеточие. Со следующей строки с отступом записываются инструкции, которые будут выполняться в случае, если условие ветвления вернёт значение «ложь». Служебные слова if и else переводятся на русский язык, как «если» и «иначе» соответственно. В языке Python, при записи инструкции ветвления, важно соблюдать отступы, иначе программа не будет работать.
Приведём пример инструкции ветвления. Предположим, что нам нужно присвоить переменной M наибольшее из значений, содержащихся в переменных a и b, или любое из значений, если они равны. Для того, чтобы это сделать, запишем инструкцию ветвления с условием: a > b. Если это условие будет выполняться, то мы присвоим переменной M значение переменной a. Если же это условие не будет выполняться, то мы присвоим переменной M значение переменной b.
if a > b:
M = a
else:
M = b
Приведённая запись инструкции ветвления называется её полной формой, но описанную задачу можно решить иначе. Для этого можно до инструкции ветвления присвоить переменной M значение переменной b. Тогда нам не нужна часть инструкции ветвления, начиная со служебного слова else. Её можно не записывать. Тогда в случае, если условие ветвления выполняется, будет выполнена инструкция, которая следует после условия, в противном случае выполнение инструкции ветвления будет завершено. Такая запись инструкции ветвления называется её сокращённой формой.
M = b
if a > b:
M = a
Решим задачу с использованием ветвлений. Треугольник на координатной плоскости задан целочисленными координатами своих вершин, не лежащих на одной прямой. Определить, является ли заданный треугольник прямоугольным.
Для решения задачи мы вычислим расстояния между вершинами треугольника. Таким образом, мы определим длины его сторон. Согласно теореме Пифагора, в прямоугольном треугольнике сумма квадратов длин двух наименьших сторон равна квадрату длины наибольшей стороны. Обратим внимание, что для проверки того, является ли треугольник прямоугольным, нам необязательно знать длины его сторон. Достаточно знать их квадраты. Таким образом в начале мы можем вычислять не расстояния между вершинами треугольника, а их квадраты. Это позволит избежать лишних вычислений.
Напишем модуль для решения задачи. С помощью инструкции print выведем на экран сообщение о том, что это программа, определяющая является ли треугольник прямоугольным. При помощи ещё одной инструкции print выведем на экран запрос на ввод координат первой вершины треугольника. Дальше запишем инструкцию считывания значений переменных x1 и y1. Так как по условию задачи координаты вершин целочисленные, то при считывании мы будем преобразовывать их значения в целочисленный тип int. Теперь дважды скопируем последние две инструкции и изменим их для ввода координат второй и третьей вершин треугольника соответственно. После того, как мы считали координаты вершин треугольника, определим квадраты длин его сторон. Для этого присвоим переменным kv_a, kv_b и kv_c соответственно квадраты расстояний между вершинами 1 и 2, 2 и 3, а также 3 и 1. Для того, чтобы определить является ли треугольник прямоугольным, нам нужно определить, какая из его сторон является наибольшей. Условимся, что наибольшей будет сторона c. Чтобы наибольшей стала сторона c, запишем две инструкции ветвления. В первой инструкции, если значение переменной kv_a больше значения kv_c, то мы поменяем их местами. Во втором ветвлении, если kv_b больше kv_c, то мы поменяем их значения местами. Теперь запишем инструкцию ветвления, определяющую, является ли треугольник прямоугольным. Его условием будет то, что сумма значений kv_a и kv_b равна значению kv_c. Если это так, то с помощью инструкции print выведем на экран сообщение о том, что заданный треугольник является прямоугольным. В противном случае мы с помощью инструкции print выведем на экран сообщение о том, что заданный треугольник не является прямоугольным.
print ('Программа, определяющая, является ли треугольник прямоугольным.')
print ('Введите координаты первой вершины треугольника.')
x1, y1 = int (input ()), int (input ())
print ('Введите координаты второй вершины треугольника.')
x2, y2 = int (input ()), int (input ())
print ('Введите координаты третьей вершины треугольника.')
x3, y3 = int (input ()), int (input ())
kv_a, kv_b, kv_c = (x2 - x1) ** 2 + (y2 - y1) ** 2, (x3 - x2) ** 2 + (y3 - y2) ** 2, (x1 - x3) ** 2 + (y1 - y3) ** 2
if kv_a > kv_c:
kv_a, kv_c = kv_c, kv_a
if kv_b > kv_c:
kv_b, kv_c = kv_c, kv_b
if kv_a + kv_b == kv_c:
print ('Заданный треугольник является прямоугольным.')
else:
print ('Заданный треугольник не является прямоугольным.')
Сохраним описанный модуль и запустим его на выполнение. Зададим вершины треугольника в точках: (1; 7), (7; 7) и (1; 1). Как видно на рисунке, данный треугольник является прямоугольным. Программа вывела на экран сообщение об этом. Снова запустим модуль на выполнение и зададим вершины треугольника в точках: (1; 7), (7; 4) и (13; 1). Очевидно, что заданный треугольник не является прямоугольным. Программа вывела сообщение об этом. Программа работает правильно. Задача решена.
Мы узнали:
· Разветвляющимися называются алгоритмы, которые содержат конструкции ветвления.
· Ветвление – это алгоритмическая конструкция, в которой, в зависимости от некоторого условия, происходит исполнение одной из двух последовательностей действий, которые называются ветвями.
· Условиями ветвлений являются логические высказывания – утверждения, истинность которых можно определить однозначно.
· Для хранения данных об истинности логических высказываний в языке Python используются переменные логического типа bool. Они могут принимать одно из двух значений: True или False.
· Для записи ветвлений в языке Python используется соответствующая инструкция, у которой есть полная и сокращённая формы.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 5302
5302

