Прямолинейное равноускоренное движение. Ускорение

Вы знаете, равномерное прямолинейное движение — это модель реального движения тел. Автомобили, корабли, самолёты и другие тела чаще всего движутся и не прямолинейно, и не равномерно. Как же описать такое движение, ведь уравнением движения мы пользоваться не можем, так как скорость тела постоянно меняется?

Для описания быстроты изменения положения тела с течением времени при неравномерном движении, вводится понятие средней скорости. Она показывает, какое перемещение в среднем совершало тело за единицу времени.

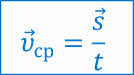
Но пользоваться этой формулой для определения модуля средней скорости можно лишь в том случае, если тело движется вдоль прямой в одну сторону. Во всех остальных случаях эта формула не работает.

Поэтому на практике пользуются понятием средней путевой скорости, с которым вы знакомы ещё с седьмого класса. Напомним, что средняя путевая скорость определяется отношением пути к промежутку времени, за который этот путь пройден. Она показывает, какой путь в среднем проходило тело за единицу времени.

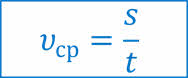
Однако следует помнить, что средняя скорость характеризует движение за весь промежуток времени в целом. Она не даёт информации о скорости движения в каждой точке траектории (или в каждый момент времени). Например, если мотоциклист преодолел путь в 300 километров за 6 часов, то средняя скорость его движения равна 50 км/ч. Иными словами, в среднем мотоциклист за каждый час проезжал 50 километров. Однако при этом он мог какое-то время стоять, какое-то время двигаться с большей или меньшей скоростью. Значит, зная среднюю скорость мотоциклиста за 6 часов, мы не сможем определить его положение через час или два.

Поэтому для описания такого движения вводится понятие мгновенной скорости, то есть скорости движения в данный момент времени или в данной точке траектории.

— А как определить мгновенную скорость тела?

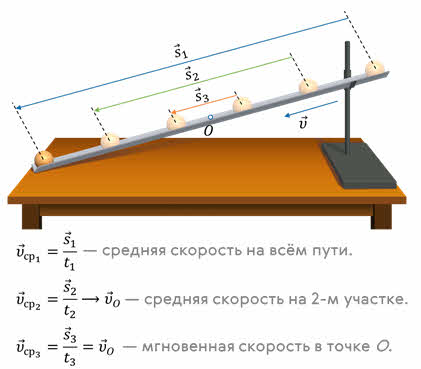
Рассмотрим пример. Пусть шарик скатывается по наклонному жёлобу. Нас интересует мгновенная скорость шарика, например, в точке О его траектории. Выделим небольшой участок траектории, включающий в себя точку О. Разделив перемещение шарика на этом участке траектории, на соответствующий промежуток времени найдём среднюю скорость перемещения на этом участке. Это именно средняя скорость, потому что скорость непрерывно изменяется, и в разных местах участка она разная. Рассмотрим меньшее перемещение — участок два. Оно произойдёт за меньший промежуток времени. Средняя скорость шарика на этом участке хотя и не равна скорости в точке О, но уже ближе к ней.

При дальнейшем уменьшении перемещений и промежутков времени мы будем получать средние скорости, которые все меньше отличаются друг от друга и от мгновенной скорости шарика в точке О. В конце концов промежуток времени станет так мал, что можно будет пренебречь изменением скорости за это время (движение станет как бы равномерным). Средняя скорость на этом участке и будет являться мгновенной скоростью шарика в точке О.

Таким образом, мгновенная скорость — это векторная физическая величина, равная отношению достаточно малого перемещения к малому промежутку времени, в течение которого это перемещение совершается:

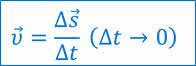
Как следует из формулы, направление мгновенной скорости совпадает с направлением движения тела. В дальнейшем мгновенную скорость мы будем называть просто скоростью.

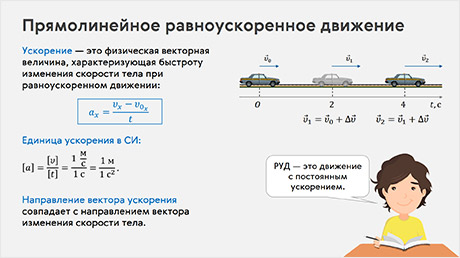
Из всех видов неравномерного движения мы будем изучать самое простое — прямолинейное равноускоренное движение. Прямолинейным равноускоренным движением называется такое движение, при котором за любые равные промежутки времени скорость тела изменяется на одну и туже величину, а траекторией движения тела является прямая линия.

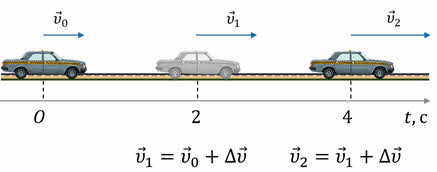
В физике существует величина, характеризующая быстроту изменения скорости тела при равноускоренном движении. Она называется ускорением и обозначается малой латинской буквой а.

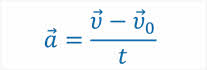
Для того, чтобы найти ускорение, необходимо найти отношение изменения скорости ко времени, в течение которого это изменение произошло. Таким образом, равноускоренное движение — это движение с постоянным ускорением.

За единицу ускорения в СИ принимается ускорение такого прямолинейного равноускоренного движения, при котором за 1 секунду скорость тела изменяется на 1 м/с:

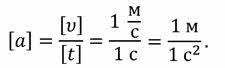
Ускорение — это векторная величина, направление которой, как следует из формулы, совпадает с направлением вектора изменения скорости тела.

Например, при разбеге самолёта направление вектора ускорения и векторов скорости совпадают и самолёт движется ускоренно. При посадке, наоборот, самолёт замедляет своё движение. В этом случае вектор ускорение и векторы скорости имеют противоположные направления. Поэтому самолёт движется замедленно.

Конечно же, как и в случае со скоростью, при решении большинства задач, мы будем пользоваться формулой, в которую входит не сам вектор ускорения, а его проекция на координатную ось.

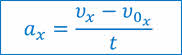
Закрепление материала.

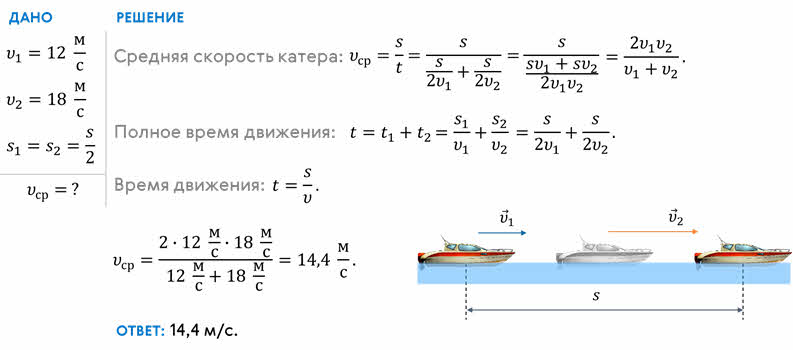
Определите среднюю скорость движения катера на участке прямолинейного пути, если первую его половину он прошёл со скоростью 12 м/с, а вторую — со скоростью 18 м/с.