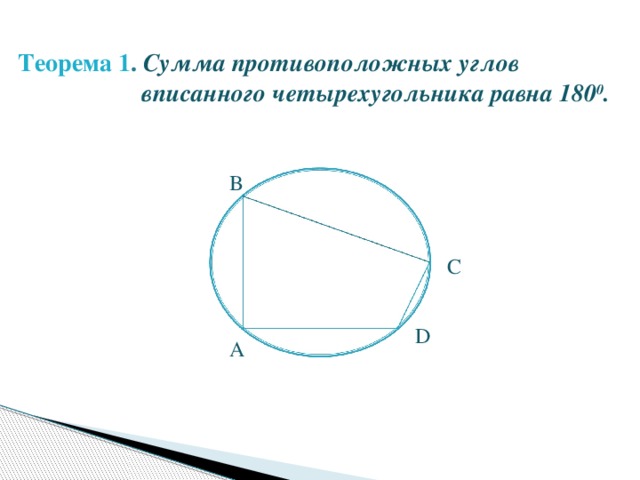
Четырехугольник, все вершины которого лежат на окружности, называется вписанным в эту окружность, а окружность называется описанной около четырехугольника.
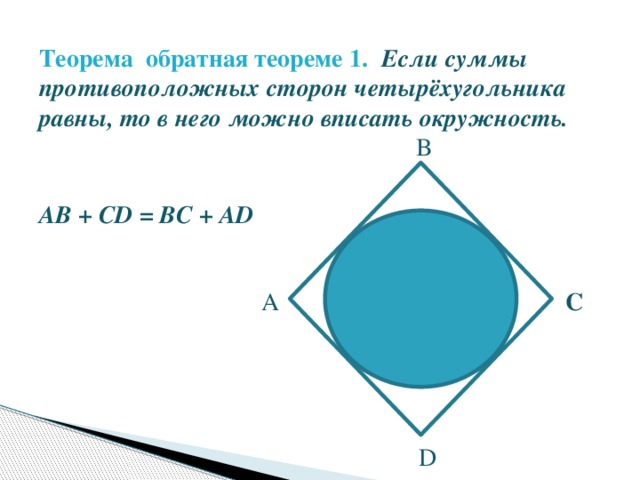
Теорема обратная теореме 1. Если сумма противоположных углов четырехугольника равна 180°, то около него можно описать окружность.

Следствие. Не во всякий четырёхугольник можно вписать окружность.
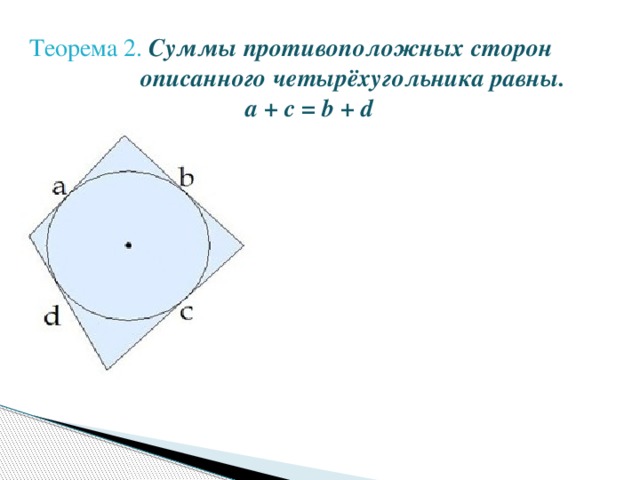
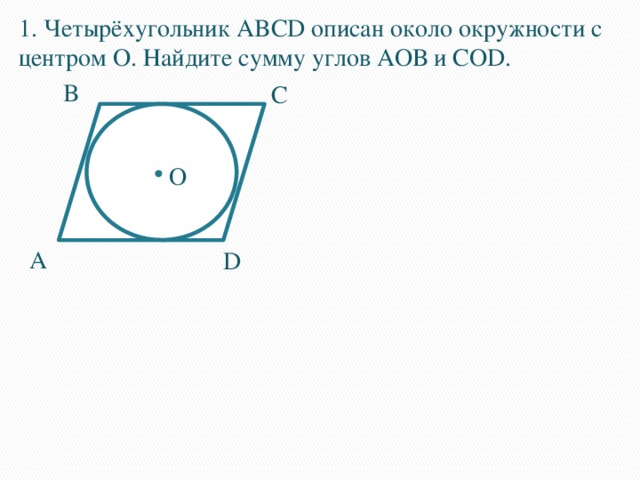
Если все стороны четырехугольника касаются окружности, то он называется четырёхугольником, описанным около этой окружности, а окружность - вписанной в четырёхугольник.
Полную информацию смотрите в файле.

 Получите свидетельство
Получите свидетельство Вход
Вход
















 Вписанные в окружность и описанные около окружности четырехугольники (презентация) (0.16 MB)
Вписанные в окружность и описанные около окружности четырехугольники (презентация) (0.16 MB)
 0
0 2572
2572 752
752 Нравится
0
Нравится
0


