Урок по теме. Непериодические бесконечные десятичные дроби.

Урок по теме. Непериодические бесконечные десятичные дроби.

Формируемые результаты:

Предметные: познакомить учащихся с понятиями бесконечной непериодической десятичной дроби, иррационального числа, действительного числа.

Личностные: формировать целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.

Метапредметные: формировать умение использовать приобретенные знания в практической деятельности.

Планируемые результаты: учащиеся научатся приводить примеры бесконечных непериодических десятичных дробей, научатся различать иррациональные и рациональные числа, действительные числа.

Тип урока: комбинированный

Оборудование. Карточки для проверочной работы. Презентация

Ход урока.

1. Организационный момент.

2. Проверка домашнего задания. 1. Устная работа

Представьте обыкновенную дробь в виде десятичной методом домножения: 1/2, 1/4, 3/4, 1/5, 3/8, 2/25, 3/50

1. Ответы на вопросы учащихся.

1. Постановка формируемых результатов и задач урока. Мотивация учебной деятельности учащихся.

2. Актуализация опорных знаний.

1.Проверочная работа по карточкам. В -1 (В -2)

1).Закончите предложения:

а) Любое рациональное число 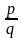разлагается в ____________.

б) Любая периодическая дробь есть десятичное разложение некоторого ____________________.

2). Запишите число в виде периодической дроби и укажите ее период:

а) 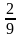( 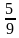); б) ( );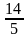

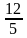3).Обратите периодическую дробь в обыкновенную: а) 0,2(3) (0,3(2)); б) 0,(31) (0, (21)).

2. Взаимопроверка.

3. Назовите пять чисел:

а) натуральных, б) положительных, в) отрицательных, г) целых, д) рациональных,
е) четных, ж) нечетных, з) простых, и) составных, к) кратных 3, л) кратных 2 и 5.

1. Изучение нового материала. Работа по презентации

1.Рассмотрим положительную бесконечную десятичную дробь 0,1011011101111…, в которой после запятой записаны цифры: единица, нуль, две единицы, нуль, три единицы, нуль и т.д. У этой дроби никакая группа цифр не является периодом. Эта дробь непериодическая, а, значит, она не является десятичным разложением какого – либо рационального числа.

2. Приведите примеры положительных бесконечных непериодических десятичных дробей.

3.Поставив перед положительной дробью знак «--», получим отрицательную дробь. Например, дроби -0,1001000100001 … является отрицательной бесконечной непериодической дробью.

4. Приведите примеры отрицательных бесконечных непериодических десятичных дробей.

5. Бесконечные десятичные дроби называют числами.

Число, которое можно записать в виде бесконечной непериодической десятичной дроби называют иррациональным (лат. irrationalis — неразумный) числом. Иррациональное число не может быть представлено в виде дроби , где n - натуральное, а m – целое числа.

6. Рациональные и иррациональные числа называются действительными числами.

Любое действительное число представляется в виде бесконечной десятичной дроби. Если число рациональное, то дробь периодическая, а если число иррациональное, то дробь непериодическая.

7

Действительные числа

1. Физкультминутка.

Вновь у нас физкультминутка

Наклонились, ну-ка, ну-ка!

Распрямились, потянулись,

А теперь назад прогнулись.

Разминаем руки, плечи,

Чтоб сидеть нам было легче,

Чтоб писать, читать, считать

И совсем не уставать.

Хоть зарядка коротка,

Отдохнули мы слегка.

1. Первичное закрепление.

1. Учебник стр. 199. В два столбика под схемой записать числа из упражнения № 990.

2. Устно №987, № 989.

3. №4 и №5 из презентации

1. Повторение.

1. Найдите приближенно сумму чисел, беря слагаемые с точностью до 0,001.

а) 4,6 + 4,(6) ≈ ; б) 2,468 – 2,3(7) ≈ .

2. Найдите результат приближенно, беря числа с точностью до второй значащей цифры.

а) 2,4 · 13,(2) ≈ ; б) 4,3 : 0,(4) ≈ .

3. Запишите результат в виде обыкновенной дроби: 0,1(2) + 0,11.

4. Решить задачу. Пылесос подорожал на 16% и стал стоить 17400 рублей. Потом он подешевел на 14%. На сколько рублей дороже стоил этот пылесос до подорожания, чем после того как он подешевел?

1. Рефлексия. Оцените активность своей работы на уроке.

На уроке я:

а) активно работал(а);

б) работал(а), но не активно;

в) был (а) пассивен (пассивна).

1. Домашняя работа: п. 5.4 № 988, 992, 866, 893 (а).

НЕПЕРИОДИЧЕСКИЕ БЕСКОНЕЧНЫЕ ДЕСЯТИЧНЫЕ ДРОБИ

Математика, 6 класс

Любое рациональное число можно представить в виде бесконечной десятичной периодической дроби.

Любая бесконечная периодическая десятичная дробь является рациональным числом.

а =0,1011011101111…

• Никакая группа цифр не является периодом

• Дробь непериодическая

Число, которое можно записать в виде бесконечной непериодической десятичной дроби, называют иррациональным

Это ссылка на видеоролик. Зажмите кнопку Ctrl и нажмите на текст.

Рациональные и иррациональные числа называются действительными числами.

ФИЗКУЛЬТМИНУТКА

№ 4 Среди записанных чисел 5; 0; 1; 6,(4); -21; 56,031; ; 4,(9); 0,777… укажите:

5; 1.

• Натуральные числа:

• Целые числа:

• Рациональные числа:

• Иррациональные числа:

• Действительные числа:

5; 0; 1; -21.

5; 0; 1; 6,(4); -21; 56,031;4,(9); 0,777…

Все числа

№ 5 Запишите по 3 числа в каждую строку

• Натуральные числа:
• Целые числа:
• Рациональные числа:
• Иррациональные числа:
• Действительные числа:

Домашнее задание

п. 5.4

№ 988, 992, 866, 893 (а).