Таблицы истинности. Решение задач

Задание 2. В следующем высказывании выделите простые, обозначив каждое из них буквой. Запишите с помощью букв и знаков логических операций каждое составное высказывание: Неверно, что Солнце движется вокруг Земли

А= Солнце движется вокруг Земли

НЕ А; NOT A; ¬A;

Задание 3. В следующем высказывании выделите простые, обозначив каждое из них буквой. Запишите с помощью букв и знаков логических операций каждое составное высказывание: Число 376 чётное и трёхзначное.

А= Число 376 чётное ; B= Число 376 трёхзначное

А И В; А & В; А • В; A AND В; A  B

Задание 4 В следующем высказывании выделите простые, обозначив каждое из них буквой. Запишите с помощью букв и знаков логических операций каждое составное высказывание: Новый год мы встретим на даче или на Красной площади .

А= Новый год мы встретим на даче ;

B= Новый год мы встретим на Красной площади

А ИЛИ В; А OR В; А V В; А | В; A + В

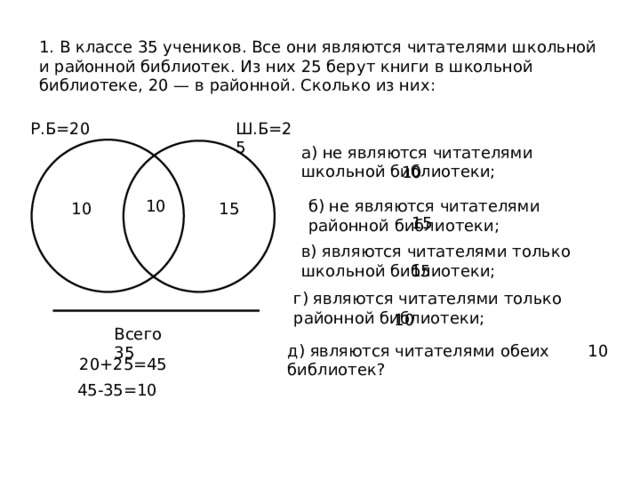
1. В классе 35 учеников. Все они являются читателями школьной и районной библиотек. Из них 25 берут книги в школьной библиотеке, 20 — в районной. Сколько из них:

Р.Б=20

Ш.Б=25

а) не являются читателями школьной библиотеки;

10

б) не являются читателями районной библиотеки;

10

15

10

15

в) являются читателями только школьной библиотеки;

15

г) являются читателями только районной библиотеки;

10

Всего 35

д) являются читателями обеих библиотек?

10

20+25=45

45-35=10

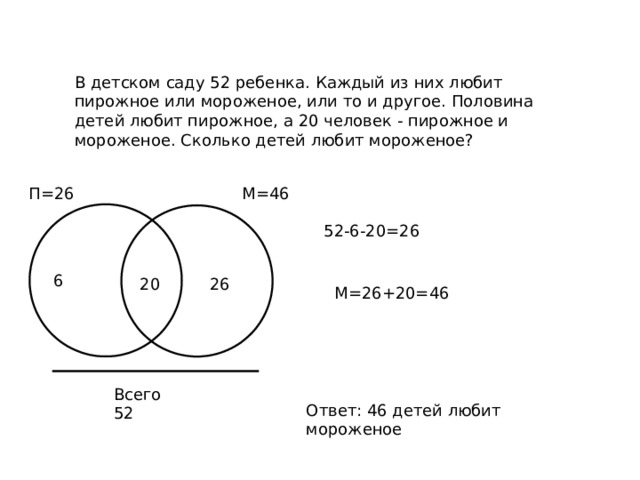
В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое, или то и другое. Половина детей любит пирожное, а 20 человек - пирожное и мороженое. Сколько детей любит мороженое?

П=26

М=46

М=?

52-6-20=26

6

20

26

М=26+20=46

Всего 52

Ответ: 46 детей любит мороженое

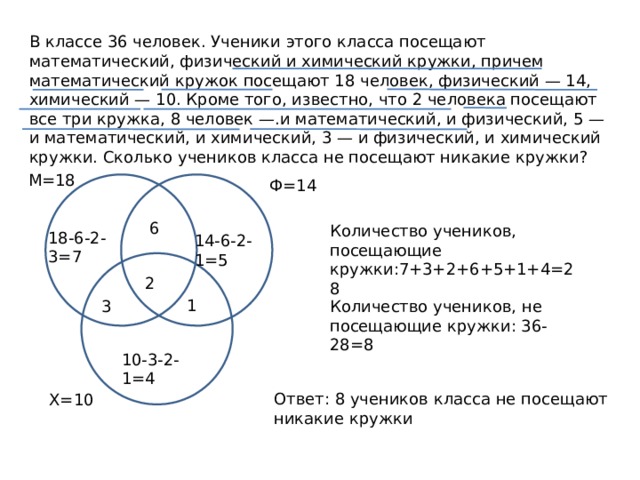
В классе 36 человек. Ученики этого класса посещают математический, физический и химический кружки, причем математический кружок посещают 18 человек, физический — 14, химический — 10. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек —.и математический, и физический, 5 — и математический, и химический, 3 — и физический, и химический кружки. Сколько учеников класса не посещают никакие кружки?

М=18

Ф=14

6

Количество учеников, посещающие кружки:7+3+2+6+5+1+4=28

18-6-2-3=7

14-6-2-1=5

2

1

3

Количество учеников, не посещающие кружки: 36-28=8

10-3-2-1=4

Ответ: 8 учеников класса не посещают никакие кружки

Х=10

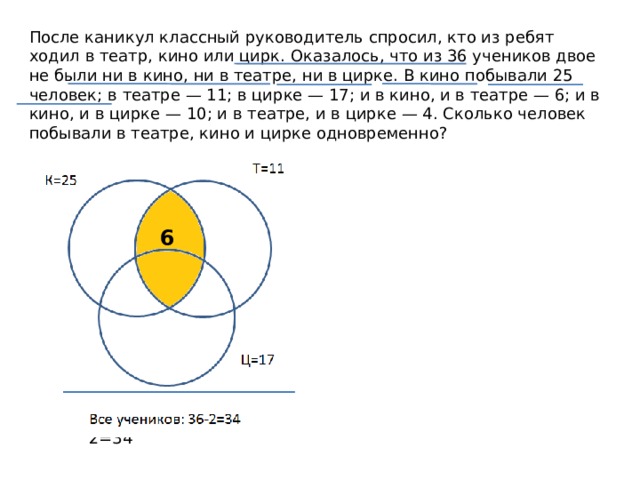
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?

Т=11

К=25

6

Ц=17

Все учеников: 36-2=34

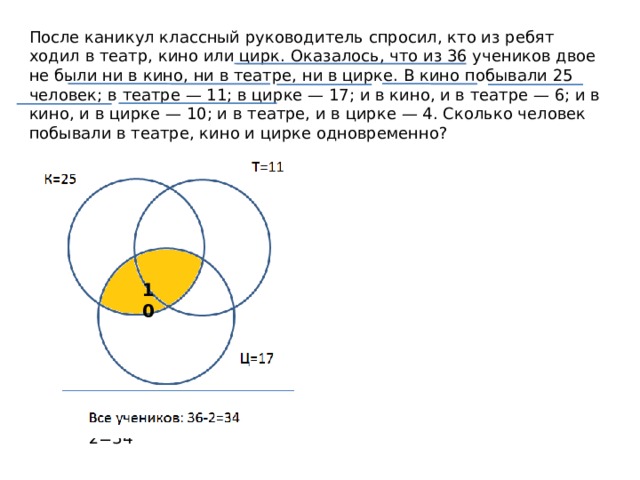
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?

Т=11

К=25

6

10

Ц=17

Все учеников: 36-2=34

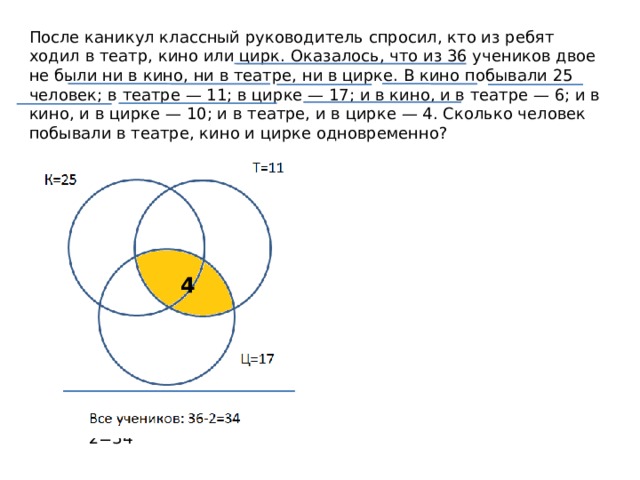
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?

Т=11

К=25

6

4

10

Ц=17

Все учеников: 36-2=34

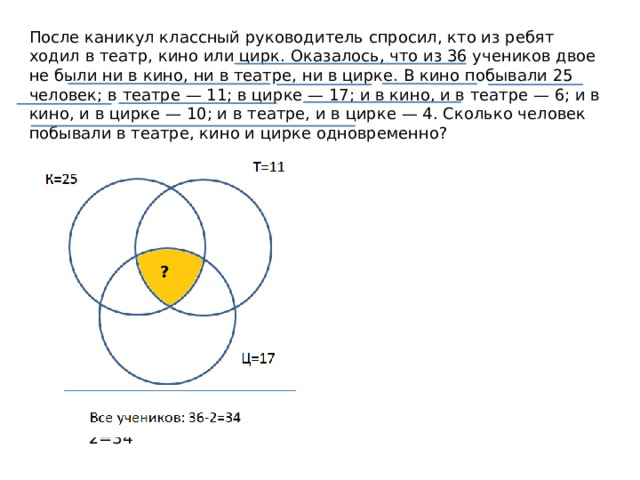
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?

Т=11

К=25

6

?

4

10

Ц=17

Все учеников: 36-2=34

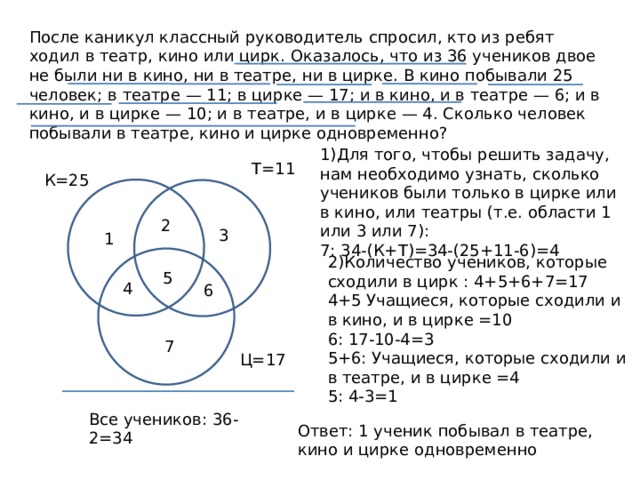
После каникул классный руководитель спросил, кто из ребят ходил в театр, кино или цирк. Оказалось, что из 36 учеников двое не были ни в кино, ни в театре, ни в цирке. В кино побывали 25 человек; в театре — 11; в цирке — 17; и в кино, и в театре — 6; и в кино, и в цирке — 10; и в театре, и в цирке — 4. Сколько человек побывали в театре, кино и цирке одновременно?

1)Для того, чтобы решить задачу, нам необходимо узнать, сколько учеников были только в цирке или в кино, или театры (т.е. области 1 или 3 или 7):

7: 34-(К+Т)=34-(25+11-6)=4

Т=11

К=25

2

3

1

2)Количество учеников, которые сходили в цирк : 4+5+6+7=17

4+5 Учащиеся, которые сходили и в кино, и в цирке =10

6: 17-10-4=3

5+6: Учащиеся, которые сходили и в театре, и в цирке =4

5: 4-3=1

5

4

6

7

Ц=17

Все учеников: 36-2=34

Ответ: 1 ученик побывал в театре, кино и цирке одновременно

Таблицы истинности

Простые и сложные высказывания

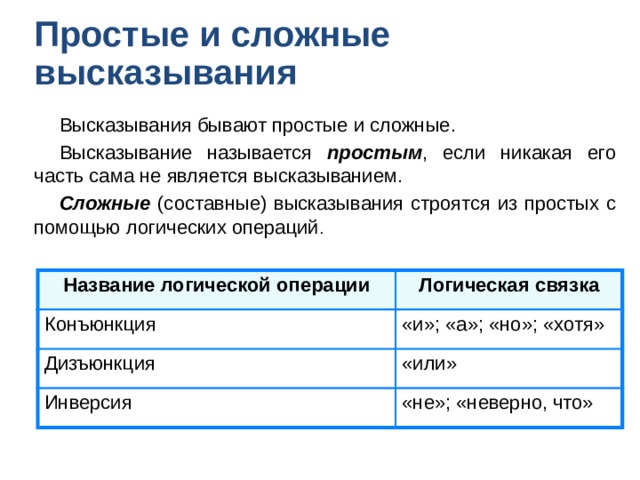
Высказывания бывают простые и сложные.

Высказывание называется простым , если никакая его часть сама не является высказыванием.

Сложные (составные) высказывания строятся из простых с помощью логических операций .

Название логической операции

Конъюнкция

Логическая связка

Дизъюнкция

«и»; «а»; «но»; «хотя»

«или»

Инверсия

«не»; «неверно, что»

Решение логических выражений принято записывать в виде таблиц истинности .

Таблица истинности – таблица, в которой по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.

Для составления таблицы необходимо:

• Выяснить количество строк в таблице (вычисляется как 2 n +1, где n – количество переменных).

• Выяснить количество столбцов = количество переменных + количество логических операций. Установить последовательность выполнения логических операций.
• Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
• Заполнить таблицу истинности по столбцам.

Приоритет выполнения логических операций следующий: то, что в скобках , инверсия (отрицание), конъюнкция (умножение), дизъюнкция (сложение) .

С помощью таблиц истинности можно проверить истинность любых сложных высказываний.

Построим таблицу истинности для выражения:

Количество строк = 2 2 (2 переменных)+ 1()заголовки столбцов=5.

Количество столбцов = 2 логические переменные (А, В) + 5 логических операций (v, &, ¬, v, ¬ )=7

A

B

Построим таблицу истинности для выражения:

Построим таблицу истинности для выражения: