Получите свидетельство
Вход
Треугольники
Треугольник – это геометрическая фигура, состоящая из трех точек , не лежащих на одной прямой и соединенная отрезками.
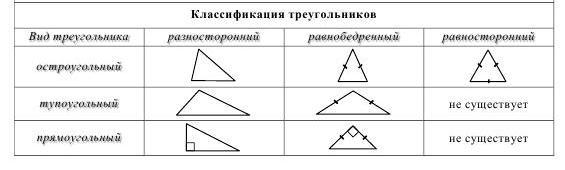
Виды треугольников
а) Прямоугольные, тупоугольные, остроугольные.
Прямоугольный треугольник – треугольник, у которого один угол – прямой, т.е. равный 90°. Остроугольный треугольник – треугольник, у которого все углы острые.
Тупоугольный треугольник – треугольник, у которого два угла острые, а третий – тупой.
б) Равнобедренные , равносторонние и разносторонние треугольники.
Треугольник , у которого все стороны равны , называют равносторонним
Треугольник , у которого две стороны равны , называют равнобедренным
Треугольник , у которого все стороны разные , называют разносторонним
Признаки равенства треугольников -
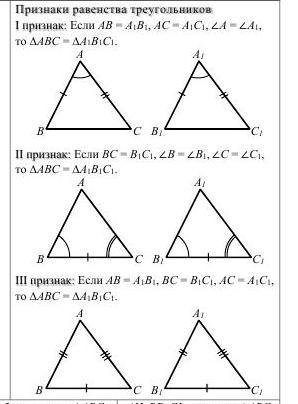
По двум сторонам и углу между ними
По стороне и двум прилежащим к ней углам
По трем сторонам.
Элементы треугольника
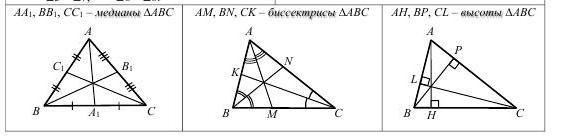
Медиана треугольника– отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.
Медианы пересекаются в одной точке и делятся этой точкой в отношении 2 : 1, считая от вершины.
Медиана делит треугольник на два равновеликих треугольника, площадь каждого из этих двух треугольников равна половине площади данного треугольника.
Биссектриса треугольника – отрезок соединяющий вершину треугольника с противолежащей стороной и делящий угол пополам.
Биссектрисы пересекаются в одной точке.
Точка, лежащая на биссектрисе угла, равноудалена от его сторон.
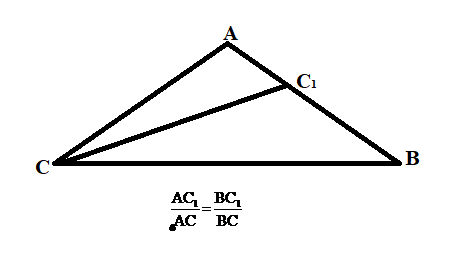
Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам.
Высота треугольника – перпендикуляр, проведенный из вершины треугольника к прямой, на которой лежит противоположная сторона.
Высоты или их продолжения пересекаются в одной точке.
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника..
Средняя линия треугольника параллельна третьей стороне и равна половине этой стороны.
Внешним углом треугольника называется угол, смежный любому углу треугольника.
Его градусная мера равна сумме двух углов треугольника, не смежных с ним.
Соотношение между сторонами и углами треугольника.
В треугольнике:
сумма углов треугольника равна 1800.
против большей стороны лежит больший угол;
против большего угла лежит большая сторона.
каждая сторона треугольника меньше суммы двух других сторон.
Неравенство треугольника
a
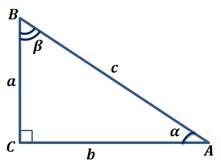
Прямоугольный треугольник
Стороны в прямоугольном треугольнике называются - гипотенуза и два катета
Сторону, которая лежит напротив прямого угла, называют гипотенузой.
Катетами называются стороны, которые образуют прямой угол.
Свойства прямоугольного треугольника
Гипотенуза больше любого катета.
Сумма острых углов в прямоугольном треугольнике равна 90°
В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы.
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета равен 30°.
Медиана, проведенная из вершины прямого угла, равна половине гипотенузы.
Высота hc, проведенная из вершины прямого угла, есть среднее пропорциональное проекций катетов на гипотенузу.
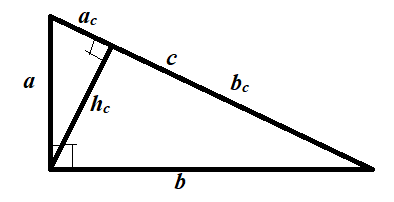Каждый катет есть среднее пропорциональное гипотенузы и своей проекции на гипотенузу.
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
c2 = a2 + b2
Признаки прямоугольного треугольника
- Если медиана треугольника равна половине стороны, к которой она проведена, то этот треугольник прямоугольный.
Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то треугольник прямоугольный.
Признаки равенства прямоугольных треугольников -
по двум катетам,
по гипотенузе и катету,
по катету и острому углу,
по катету и гипотенузе.
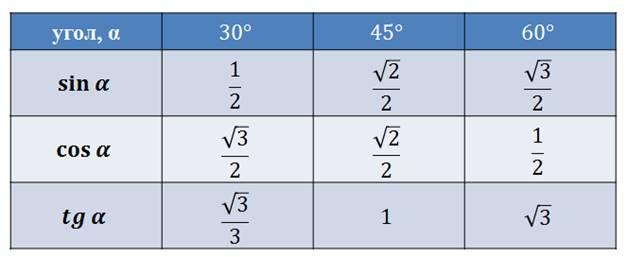
Тригонометрические функции острого угла прямоугольного треугольника
Отношения сторон прямоугольного треугольника не зависят от величин этих сторон, а зависят от величины острых углов прямоугольного треугольника. Для этих отношений были введены специальные названия и обозначения(тригонометрические функции).
Определение:
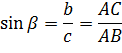синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
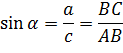
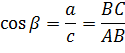косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
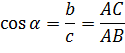
тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
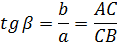
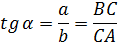
Тригонометрические равенства
Основное тригонометрическое тождество
sin α = cos
Связь между сторонами и углами в прямоугольном треугольнике
Катет, лежащий против острого угла, равен произведению гипотенузы на синус острого угла.
Катет, прилежащий к острому углу, равен произведению гипотенузы на косинус острого угла.
Катет, лежащий против острого угла, равен произведению второго катета на тангенс острого угла.
Гипотенуза прямоугольного треугольника равна отношению противолежащего катета к синусу острого угла.
Гипотенуза прямоугольного треугольника равна отношению прилежащего катета к косинусу острого угла.
Равнобедренный треугольник
Равнобедренный треугольник – треугольник, у которого две стороны равны.
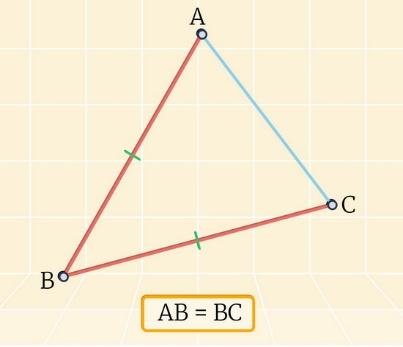
AB = BC.
∆ABC – равнобедренный.
В равнобедренном треугольнике равные стороны называются боковыми, а третья сторона – основанием.
AB и BC – боковые стороны ∆ABC, AC – основание ∆ABC.
Свойства равнобедренного треугольника
В равнобедренном треугольнике углы при основании равны.
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой треугольника.
Высота равнобедренного треугольника, проведённая к основанию, является медианой и биссектрисой.
Медиана равнобедренного треугольника, проведённая к основанию, является высотой и биссектрисой.
Площадь треугольника.
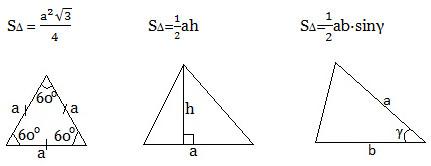
Формула Герона
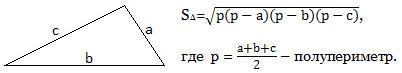
Площадь прямоугольного треугольника.
SΔ=(½) a∙b, где a и b — катеты или SΔ=(½) c∙h, где с — гипотенуза, h –высота, проведенная к гипотенузе.
Подобие треугольников
Подобие – это преобразование, при котором расстояние между точками изменяется в одно и то же число раз. Преобразование подобия сохраняет градусные меры углов.
Треугольники называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Признаки подобия треугольников:
1 признак – по двум углам (если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны);
2 признак - по двум сторонам и углу между ними (если 2 стороны одного треугольника пропорциональны 2 сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны);
3 признак – по трем сторонам (если все стороны одного треугольника пропорциональны всем сторонам другого треугольника, то такие треугольники подобны).
Если треугольники подобны, то у них соответствующие углы равны, а стороны пропорциональны.
Справочный материал "Треугольники" (173.15 KB)
0
3019
27
Нравится
0
